Gelöste Aufgaben/W8Zt

Aufgabenstellung

Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:

Caption

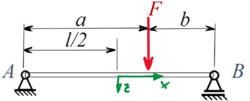
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten.

Üblich ist bei Verfahren von Rayleigh-Ritz nämlich sonst das Prinzip vom Minimum der Potentiellen Energie. Die Lösung nach dem Standardverfahren finden Sie hier in W8Zu.

Lösung mit Maxima

Mit dem Föppl-Symbol "<>", sowie

$\alpha =a/\ell$, $\beta =1-\alpha$ und $\xi =x/\ell$

ist die analytische Lösung:

$EIw(x)=\frac{F{\ell }^3}{6}[\beta \xi (1-{\beta }^2-{\xi }^2)+<\xi -\alpha {>}^3]$.

Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!

Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems.

Header

Hier arbeiten wir mit Maxima.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2017-09-14                            */
/* ref: TM-C, Labor 3 - aus Gross, Augf. TM 2,Biegestab*/
/* description: finds the approx. solution employing   */
/*              two polynomial trialfunctions          */
/*******************************************************/

Declarations

Wir definieren zunächst die Symbole für die virtuellen Arbeiten und die virtuellen Verrückungen - die in Maxima nicht standardmäßig verfügbar sind.

Die Annahme ℓ>0 brauchen wir, damit Maxima Wurzel-Ausdrücke mit diesem Parameter richtig vereinfachen kann.

/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δV", alphabetic);
declare("δΨ", alphabetic);
declare("δw", alphabetic);

/* declarations */
assume(l>0);

Formfunctions

Als unabhängige Koordinaten des Balkens wählen wir "x" entlang der Neutralen Faser mit Ursprung in der Mitte zwischen A und B.

Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems und deren Variationen (δ)

$\underset{\_}{Q}=\left(\begin{array}{c}V\\ \mathrm{\Psi }\end{array}\right),\delta \underset{\_}{Q}=\left(\begin{array}{c}\delta V\\ \delta \mathrm{\Psi }\end{array}\right),$

Koordinaten

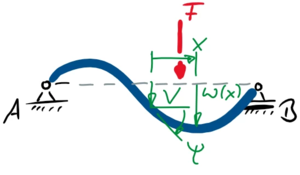
und wählen V und ψ  als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt x=0 des Balkens.

Jetzt brauchen wir zwei Ansatzfunktionen, die unseren Koordinaten V und ψ entsprechen. Wir wollen diese beiden anschaulich denken können - wir wählen einfache Polynome: eine achsensymmetrische und eine punktsymmetrische Funktion mit den noch unbestimmten Konstanten c_ij:

• $v_1\left(x\right):=c_{1,2}\cdot x^2+c_{1,0}$
• $v_2(x):=c_{2,3}\cdot x^3+c_{2,1}\cdot x$

Diese beiden Funktionen müssen

1. Geometrische Randbedingungen erfüllen und
2. jeweils mit den Koordinaten V und ψ  verknüpft werden.

Die zugehörigen Gleichungen (= die Randbedingungen) sind

• $c_{1,0}=V,\frac{c_{1,2}\cdot {\ell }^2}{4}+c_{1,0}=0$ und
• $c_{2,1}=\mathrm{\Psi },\frac{c_{2,3}\cdot {\ell }^3}{8}+\frac{c_{2,1}\cdot \ell }{2}=0$

mit der Lösung

$c_{1,0}=V,c_{1,2}=-\frac{4\cdot V}{{\ell }^2},c_{2,1}=\mathrm{\Psi },c_{2,3}=-\frac{4\cdot \mathrm{\Psi }}{{\ell }^2}$

Anstatt der exakten, bekannten Lösung, verwenden wir in diesem Näherungsansatz also nun die Funktion

$\mathrm{w}\left(x\right)=-\frac{4\cdot x^2\cdot V}{{\ell }^2}+V-\frac{4\cdot \mathrm{\Psi }\cdot x^3}{{\ell }^2}+\mathrm{\Psi }\cdot x$,

Trial-Functions

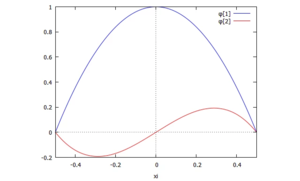
die beiden Koordinaten V und ψ müssen wir noch bestimmen. Die Funktionen, die zu V und ψ gehören, sind rechts aufgetragen:

Klar ist: die exakte Lösung dieses Lastfalls ist eine Funktion, die im Querkraftverlauf am Kraftangriffspunkt (x=a - ℓ/2) einen Sprung hat. Dagegen ist der Querkraftverlauf unserer Näherungslösung stetig differenzierbar und obendrauf noch konstant!

/**** define form functions ***/
/* coordinates */
coords : [[V,Psi], [δV,δΨ]];	

/* generic polynomials */
define(v[1](x),sum(c[1,2*i]*x^(2*i),i,0,1));
define(v[2](x),sum(c[2,(2*i+1)]*x^(2*i+1),i,0,1));

/* solve for c's to comply with geometric boundary conditions      */
coeffs : append(solve([v[1](0)=V,v[1](+l/2)=0],[c[1,0],c[1,2]])[1],
                solve([subst([x=0],diff(v[2](x),x))=Psi,v[2](+l/2)=0],[c[2,1],c[2,3]])[1]);

/* employ in polynomials */
forms : [w(x)  = expand(subst(coeffs, sum(v[i](x),i,1,2)))];
forms : append(forms,
                 [δw(x) = subst(makelist(coords[1][i]=coords[2][i],i,1,2),subst(forms,w(x)))]);
trials: subst([x=l*xi],makelist(coeff(subst(forms,w(x)), coords[1][i]),i,1,2));

plot2d( [trials[1],trials[2]/l],[xi,-1/2,+1/2], [legend, "φ[1]","φ[2]"]);

Equilibrium Conditions

Mit dem Prinzip der virtuellen Verrückungen ist die Gleichgewichtsbedingung immer

$\delta W=\delta A-\delta \mathrm{\Pi }$

Mit den Beiträgen

$\delta A=F\cdot \delta w\left(x_F\right),\delta \mathrm{\Pi }=\underset{-\frac{\ell }{2}}{\overset{\frac{\ell }{2}}{\int }}(\frac{d^2}{d{x}^2}\cdot w\left(x\right))\cdot (\frac{d^2}{d{x}^2}\cdot \delta w\left(x\right))dx\cdot EI$

und dem Einsetzen der Ansatzfunktionen und deren Variation finden wir

$\begin{array}{ll}\delta W=& -\frac{(64\cdot EI\cdot V+({\alpha }^2-1)\cdot {\ell }^3\cdot F)}{{\ell }^3}\cdot \delta V\\ & +\frac{{\ell }^2\cdot (\alpha \cdot ({\alpha }^2-1)\cdot {\ell }^2\cdot F+96\cdot \mathrm{\Psi }\cdot EI)}{2\cdot {\ell }^3}\cdot \delta \mathrm{\Psi }\end{array}$

Achtung: hier bezeichnet nun α=-1 den Punkt A, α=+1 den Punkt B.

Diese virtuelle Arbeit des Gesamtsystems spalten wir jetzt nach den virtuellen Verrückungen auf und erhalten zwei unabhängige Gleichungen in V und ψ:

$\begin{array}{cc}-\frac{({\alpha }^2-1)\cdot {\ell }^3\cdot F+64\cdot EI\cdot V}{{\ell }^3}& =0\\ -\frac{96\cdot \mathrm{\Psi }\cdot EI+({\alpha }^3-\alpha )\cdot {\ell }^2\cdot F}{2\cdot \ell }& =0\end{array}$

Und die können wir leicht lösen:

/* Virtual Work of system (equilibrium condition) */
parts : [/* virtual work of implied external force F*/
         δA = F*δw(x[F]),
         /*virt. strain energy*/
         δΠ = integrate(EI*diff(w(x),x,2)*diff(δw(x),x,2),x,-l/2,+l/2)];
parts : subst([δw(x[F]) = subst([x=\alpha*l/2], subst(forms,δw(x)))],parts);
parts : subst(forms,parts);

PvV : δW = δA-δΠ;
PvV : subst(forms,subst(parts,PvV));
/* execute differntiation and integration of δW */
PvV : expand(ev(PvV,nouns));

/* pick individual equations */
equs : makelist(coeff(subst(PvV,δW),coords[2][i]),i,1,2);

Solve

In Matrix-Schreibweise stellen wir diesen Ausdruck gewöhnliches lineares Gleichungssystem dar:

$\underset{\_}{\underset{\_}{A}}\cdot \underset{\_}{x}=\underset{\_}{b}$

mit

$\underset{\_}{\underset{\_}{A}}=EI\cdot \left(\begin{array}{cc}-\frac{64}{{\ell }^3}& 0\\ 0& -\frac{48}{\ell }\end{array}\right),\underset{\_}{b}=F\cdot ({\alpha }^2-1)\cdot \left(\begin{array}{c}1\\ \frac{\alpha \cdot \ell }{2}\end{array}\right)$

sieht das Gleichungssystem wieder handlich aus, die Lösung ist:

$V=-\frac{({\alpha }^2-1)\cdot {\ell }^3}{64\cdot EI}\cdot F,\mathrm{\Psi }=-\frac{({\alpha }^3-\alpha )\cdot {\ell }^2}{96\cdot EI}\cdot F$

⚠ Und wissen Sie auch ....:

... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Koeffizienten bzgl. von α an - was erkennen Sie?

/* Mathematical Model */
ACM : augcoefmatrix(equs,coords[1]);
/* ordinary lineary system of equations*/
ole : [A = submatrix(ACM,3), b = -col(ACM,3)];
/* -> here we employ the shortcut via "solve" */
sol: solve(equs,coords[1])[1];

Post-Process

Die Lösung normieren wir noch für das Post-Processing mit dem Fakto s - der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn F in der Mitte zwischen A und B angreift):

$s=\frac{{\ell }^3}{48EI}\cdot F$

Wir tragen sie für verschiedene Kraft-Angriffspunkte (α=-1,...α=+1) auf:

Parameterstudie: Auslenkung w(a) des Kraft-Einleitungspunktes

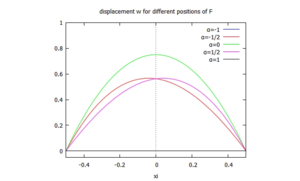
/* plot results */
m : 2; scale : F*l^3/(EI*48);
leg : append([legend],makelist(simplode(["α=",(-m+i)/m]),i,0,2*m));
plotfct : expand(subst([x=xi*l],subst(sol,subst(forms,w(x)/scale))));
toplot : makelist(subst([alpha=(-m+i)/m],plotfct),i,0,2*m);
plot2d(subst([alpha=0],toplot),[xi,-1/2,+1/2], [y,-0.05,1.0], leg,
		[title, "displacement w for different positions of F"]);

Post-Process - Vergleich mit analytischer Lösung

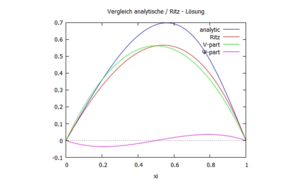
Und wir schauen uns für α=1/2 die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an:

Vergleich der Biegelinie für analytische / numerische Lösung

✔ Und wissen Sie auch ...:

... wie der Verlauf der Querkraft im Vergleich Ritz / analytisch aussieht?

/* Vergleich mit analytischer Lösung */
foppl(xi,alpha) := if (xi < alpha) then 0 else xi-alpha;
anplot : F*l^3/(6*EI)*(beta*xi*(1-beta^2-xi^2)+foppl(xi,alpha)^3)/scale;
anplot : subst([beta=1-alpha],anplot);
ritz: subst([xi=xi-1/2],subst(alpha=1/2,expand(subst(sol,makelist(trials[i]*coords[1][i]/scale,i,1,2)))));

plot2d([subst([alpha=3/4],anplot),ritz[1]+ritz[2], ritz[1],ritz[2]],[xi,0,1],
        [legend, "analytic", "Ritz", "V-part", "Ψ-part"],
        [title, "Vergleich analytische / Ritz - Lösung"])

---

<Links

• ...

Literature

• ...