Gelöste Aufgaben/SKER
Aufgabenstellung
Die Bewegung des Dehnstabes wird durch das Zusammenspiel von elastischen Verformungen und Trägheitskräften bestimmt. Man nennt das "Schwingungen von Kontinua" - diese untersuchen wir hier. Der zentrale Aufgabe besteht in der Berechnung der homogenen Lösung - und der Anpassung der Lösungsanteile an die Anfangsbedingungen.
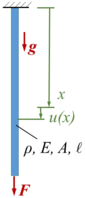
Gesucht ist analytische Lösung für Schwingungen des Euler-Bernoulli-Balkens beim Loslassen aus der enspannten Ruhelage.
Lösung mit Maxima
Header
Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass
.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-01-17 */
/* ref: oscillations of continuous media */
/* description: analytic solutioun for Extension Rod */
/*******************************************************/
/* settings */
workdir: "C:\\Users\\X...X\\plots\\";
/* assumptions */
assume(E>0,A>0,l[0]>0);
Equations of Motion
In der Gleichgewichtsbeziehung für den Dehnstab setzen wir als eingeprägte, äußere Streckenlast n(x,t) die D'Alembert'sche Trägheitskraft und die Gewichtskraft an, also
Die Lösung der partiellen Bewegungsgleichung
setzt sich dann aus zwei Lösungsanteilen, der partikularen Lösung up und der homogenen Lösung uh, zusammen; wir schreiben
- .
/*******************************************************/
/* analytical solution for equations of motion */
eom : 'E*A*diff(u(x,t),x,2)-rho*A*'diff(u(x,t),t,2) = rho*A*g;
Particular Solution
Die partikulare Lösung up erfüllt die "rechte Seite" der Bewegungsgleichung, also -ϱ A⋅g:
- .
Die rechte Seite ist zeit-unveränderlich - so auch die partikulare Lösung:
Wir integrieren die Bewegungsgleichung zwei Mal und erhalten
- .
Die zwei Integrationskonstanten Ci müssen wir nun an die Randbedingungen
anpassen, wir erhalten aus dem linearen Gleichungssystem
und damit die partikulare Lösung
Und so sieht up aus:
/***************************************************************************/
/* p a r t i c u l a r s o l u t i o n */
/***************************************************************************/
u[p] : subst([%c1=C[1],%c2=C[0]],integrate(integrate(E*A*diff(u(x),x,2)=-rho*A*g,x),x));
u[p] : subst(solve([subst([x= 0 , u(0) =0], u[p]),
subst([x=l[0], diff(u(l[0]),l[0])=0],diff(u[p],x))],[C[0],C[1]])[1],u[p]);
u[p] : solve(u[p],u(x));
/* system parameters and dimensionless time tau */
params: [t = T*tau, u[s] = subst([x=l[0]],subst(u[p],u(x)))];
plot2d(ratsimp(subst([x=xi*l[0]],subst(params,subst(u[p],u(x))/u[s]))),[xi,0,1], [y,-0.1,1.1],
[legend, "static solution"],
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "u →"])$
Homogeneous Solution
Die homogene Bewegungsgleichung
lässt Lösungen vom Typ
zu, die alle Rand- und Anfangsbedingungen erfüllen. Eigentlich müsste hier ein -Ansatz stehen, beim dem auch U komplex wäre. Mit etwas Erfahrung dürfen wir es uns hier einfacher machen.
Einsetzten unseres speziellen Ansatzes liefert
- .
Die Anpassung an die Randbedingungen
gestaltet sich einfach: unser besonderer Ansatz erfüllt bereits die erste Randbedingung (sin(0)=0), die zweite Randbedingung cos(κl)=0 ist erfüllt, wenn
- ,
wir bekommen für jedes i eine Lösung, also unendlich viele.
Zu jedem κ gehört eine Eigenkreisfrequenzen
- .
Die unterste Eigenfrequenz nutzen wir, um eine Bewegungsgleichungen dimensionslos zu machen: die längste Schwingungsperiode ist damit die Bezugs-Zeit
Die Lösungen
mit Ihren Modal-Formen ϕi und Eigenkreisfreuquenzen ω0,i sind hier aufgetragen.
| Mode | Modalform ϕj | Mode | Modalform ϕj |
|---|---|---|---|
| #1 | 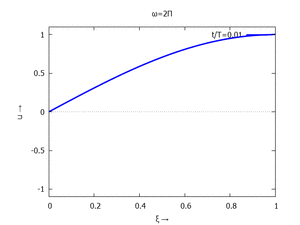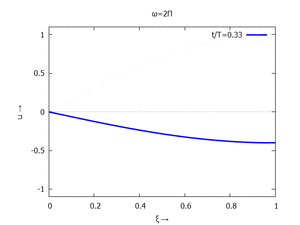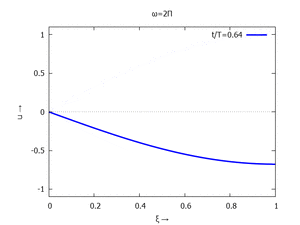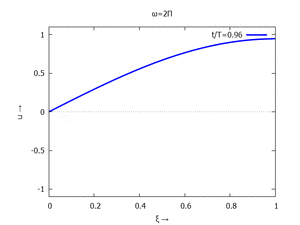 |
#2 | 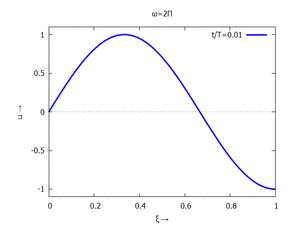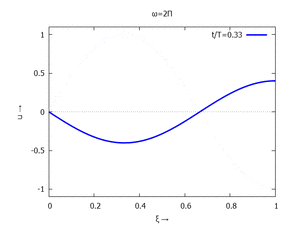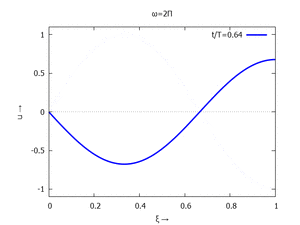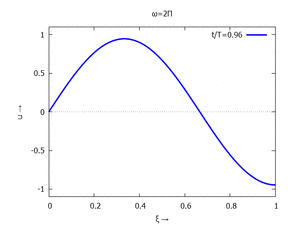 |
| #3 | 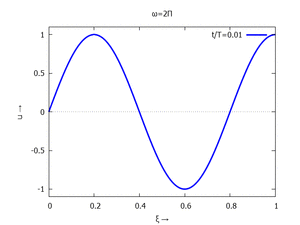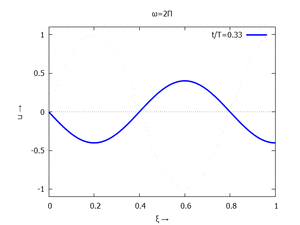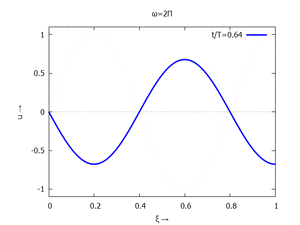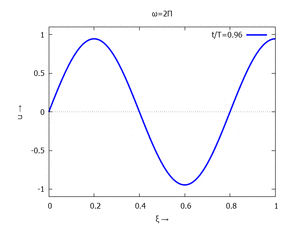 |
#4 | 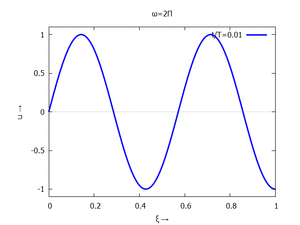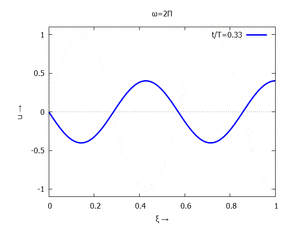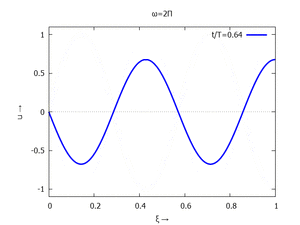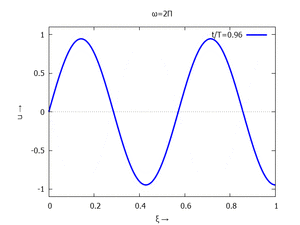 |
| #5 | 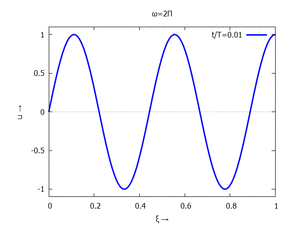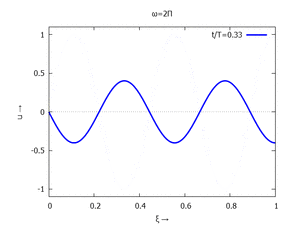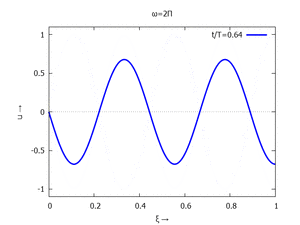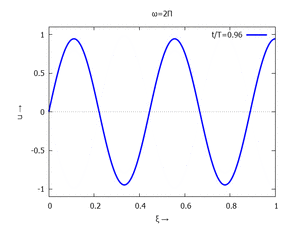 |
#6 | 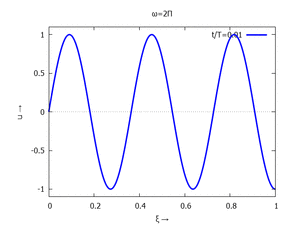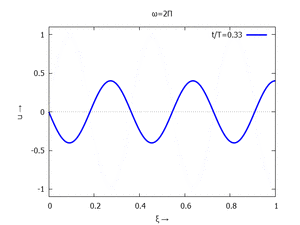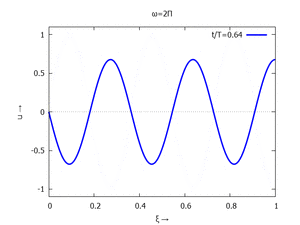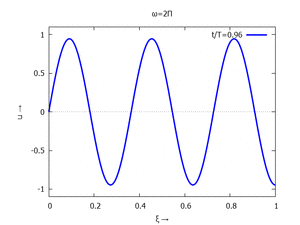 |
/***************************************************************************/
/* h o m o g e n e o u s s o l u t i o n */
/***************************************************************************/
ansatz: u(x,t) = U * sin(kappa*x) * cos(omega[0]*t);
eom : subst(ansatz,eom);
eom : ratsimp(subst(ansatz,ev(eom,nouns)/u(x,t)));
/* boundary conditions */
sol[1] : solve(kappa*l[0] = (2*i-1)*%pi/2,kappa)[1];
sol[1] : [sol[1],ratsimp(solve(subst(sol[1],eom),omega[0]^2)[1])];
/* abbreviations */
abbrev : [omega[0,0]=2*%pi/T, omega[0,0]^2= subst([i=1],subst(sol[1],omega[0]^2))];
abbrev : append(abbrev, solve(abbrev,[omega[0,0],T])[2]);
/* plot snapshots for animation */
/* create png-figures for animation */
toPlot : makelist(subst([E=1,i=j],subst(abbrev,subst([x=xi*l[0], t=T*tau],
subst([omega[0]=sqrt(subst(sol[1],omega[0]^2))],
subst(sol[1],subst([omega[0]*t=2*%pi*tau],
subst(ansatz,u(x,t)/U))))))),j,1,6);
titles : makelist(simplode(["ω=",sqrt(ratsimp(subst([i=j],subst(abbrev,
subst(sol[1],omega[0]^2*T^2)))))/%pi,"Π"]),j,1,6);
fpprintprec: 3$
NSteps : 19$
for mode:1 thru 6 do
for j:0 thru NSteps-1 do
(tstep : simplode([if j<10 then "0" else "",j]),
plot2d(subst([tau=j/NSteps],toPlot[mode]),[xi,0,1], [y,-1.1,1.1],
[title, titles[1]], [legend, simplode(["t/T=",float(j/NSteps+0.01)])],
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "u →"],
[png_file,simplode([workdir,"mode-",mode,"-step-",tstep,".png"])]))$
/* lowest eigenfreuquency */
print(omega[0,0] = sqrt(subst([i=1],subst(sol[1],omega[0]^2))));
Adapt to Initial Conditions
Zum Zeitpunkt t=0 soll
gelten. Das kriegen wir hin, indem wir die (unendlich vielen) Ui der homogenen Lösung passend wählend. Das klingt komplizierter als es ist - die Mathematik bereitet uns den Weg.
| ⚠ Spezieller Lösungsansatz: |
| Wir können unseren speziellen Lösungsansatz mit übrigens nur deshalb an die Anfangsbedingungen anpassen, weil die Anfangsgeschwindigkeit des Stabes Null ist - das liefert der cos. Für eine von Null verschiedene Anfangsgeschwindigkeit bräuchten wir den sin-Anteil der Lösung. |
Die Beziehung oben multiplizieren wir mit einer der Modalformen ϕk und bilden das Integral über die Balken-Lange ℓ, also
- .
Wir projizieren also die Modalformen auf sich selbst und auf die partikulare Lösung. Und nutzen aus, dass diese Faltungs-Integrale der Modalformen eine besondere Eigenschaft haben:
Man sagt: die Funktionen sind zueinander verallgemeinert orthogonal. Damit berechnen wir
- ,
Anhand der numerischen Werte der Koeffizienten
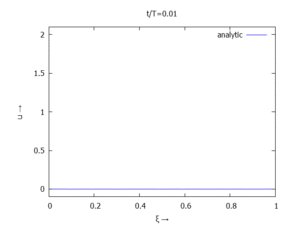
sehen wir, dass nur die erste Modalform einen signifikanten Beitrag bei der Anpassung an die Anfangsbedingungen liefert. Wir nehmen bei der Auftragung der Gesamtlösung wt(x,t) trotzdem die ersten sechs Modalformen mit:
In der Animation sehen Sie das Loslassen des Stabes aus der unverformten, geraden Referenzlage für genau eine Periodenlänge T1 der ersten Modalform. Die Schwingung, die entsteht ist T1-periodisch - die anderen Modalformen leisten einen (kleinen) Beitrag, dessen Schwingungsperiode genau ein Vielfaches der Grundschwingung ist - die Darstellung der aneinandergestückelten Lösungen geht "ruckfrei" nach einer Periode ineinander über.
/***************************************************************************/
/* t o t a l ( c o m p o s e d ) s o l u t i o n */
/***************************************************************************/
declare(i,integer);
u[p] : append(u[p],
ratsimp(solve(subst(sol[1],integrate(subst(params,subst(u[p],u(x)/u[s]))*sin(kappa*x) + U[i]*sin(kappa*x)*sin(kappa*x)=0,x,0,l[0])),U[i])));
/* analytiv solution */
analytic : append(sol[1],
[omega[0]*t = sqrt(ratsimp(subst(abbrev,(subst(sol[1],omega[0]^2*T^2)))))*tau,
x=l[0]*xi]);
sol[2] : append([ratsimp(subst([x=xi*l[0]],subst(params,subst(u[p],u(x)/u[s]))))],
makelist(subst([i=j],subst(u[p],subst(analytic,U[i]*sin(kappa*x)*cos(omega[0]*t)))),j,1,10));
/* plot snapshots for animation of total solution */
NSteps : 19$
fpprintprec: 4$
for j:0 thru 1*NSteps-1 do
(tstep : simplode([if j<10 then "00" elseif j<100 then "0" else "",j]),
plot2d(subst([tau=j/NSteps],sum(sol[2][i],i,1,length(sol[2]))),[xi,0,1], [y,-0.1,2.1],
[title, simplode(["t/T=",float(j/NSteps+0.01)])], [legend, "analytic"],
[style, [lines,1,1]], [xlabel, "ξ →"], [ylabel, "u →"],
[png_file,simplode([workdir,"initial-value-solution-step-",tstep,".png"])]))$
| ✔ Tipp: |
| Die Grundform der homogenen Differentialgleichung
ist Basis für alle Musik-Instrumente - ob Saiten- oder Blas-Instrument. Denn die Bewegungsgleichung von Saiten- und Luft-in-Rohr-Resonanzen führen auf genau diese Bewegungsgleichung. Überlegen Sie, welche Eigenschaft der homogenen Lösung dieser Bewegungsgleichung ihre besondere Bedeutug ausmacht! |
Links
- Schwingungen von Kontinua eines Euler-Bernoulli-Balkens (SKEB)
Literature
- ...
