Gelöste Aufgaben/Buck

Aufgabenstellung

Bei der Modellbildung für das Knicken von Stäben - also dem Stabilitätsverlust von Stäben durch seitliches Ausweichen unter axialer Druckbeanspruchung - gehen die Ansätze in Lehrbüchern und für Anwendungen in Finite-Elemente-Methoden unterschieldliche Wege.

Caption

Gesucht sind die Ansätze für die Berechnung der kritischen Drucklast, ausgehend von

• dem Kräfte-Gleichgewicht am ausgelenkten Stab und
• dem Prinzip der virtuellen Verrückungen mit großen Dehnungen.

Das sehen wir uns für den ersten Eulerschen Knickfall genauer an und vergleichen die Ergebnisse. Der homogene Stab mit mit dem Elastizitätsmodul $E$ hat die Länge $\ell$, einen Kreisquerschnitt mit der Querschnittsfläche $A$ und dem Flächenmoment zweiten Grades $I$. Ziel ist es, die Vorgehensweisen beider Ansätze im Vergleich darzustellen. Der Fokus liegt dabei auf der Anwendung für Finite-Elemente-Methoden - also dem Prinzip der virtuellen Verrückungen mit großen Dehnungen.

Ansatz mit dem Kräftegleichgewicht am ausgelenkten System

Für das Verständnis des Phänomens "Knicken" ist es sinnvoll, die Zusammenhänge zwischen Koordinaten und Kräften anhand von Überlegungen zum Kräftegleichgewicht aufzuzeigen.

Gleichgewicht am Stabelement

Dafür gehen wir von einem Stabelement der Länge $\mathrm{\Delta }x$ aus und tragen die Koordinaten $w(x),\phi (x)$ sowie die Schnittlasten $N(x),Q(x),M(x)$ in einem Freikörperbild an:

Schnittlasten am ausgelenkten Stab-Element.

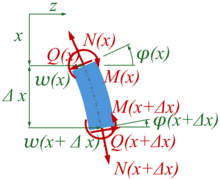
Die Gleichgewichtsbedinungen am Element liefern

$\begin{array}{lllll}\sum F_{x,i}& =& 0& :& N(x+\mathrm{\Delta }x)\cos (\phi (x+\mathrm{\Delta }x))-N(x)\cos (\phi (x))-Q(x+\mathrm{\Delta }x)\sin (\phi (x+\mathrm{\Delta }x))+Q(x)\sin (\phi (x))=0,\\ \sum F_{z,i}& =& 0& :& Q(x+\mathrm{\Delta }x)\cos (\phi (x+\mathrm{\Delta }x))-Q(x)\cos (\phi (x))+N(x+\mathrm{\Delta }x)\sin (\phi (x+\mathrm{\Delta }x))-N(x)\sin (\phi (x))=0,\\ \sum M^{x+\mathrm{\Delta }x}& =& 0& :& M(x+\mathrm{\Delta }x)-M(x)+N(x)\sin (\phi (x))\mathrm{\Delta }x-N(x)\cos (\phi (x))(w(x+\mathrm{\Delta }x)-w(x))+Q(x)\cos (\phi (x))\mathrm{\Delta }x+Q(x)\sin (\phi (x))(w(x+\mathrm{\Delta }x)-w(x)).\end{array}$

Teilen durch $\mathrm{\Delta }x$ und der Grenzwert-Übergang von $\mathrm{\Delta }x\to dx$ liefert die differentiallen Gleichgewichtsbedingungen

$\begin{array}{l}\frac{d}{dx}(N\cos (\phi ))-\frac{d}{dx}(Q\sin (\phi ))=0\\ \frac{d}{dx}(Q\cos (\phi )+\frac{d}{dx}(N\sin (\phi )=0\\ \frac{d}{dx}\left(M\right)+N\sin (\phi )+Q\cos (\phi )+\frac{d}{dx}w(-N\cos (\phi )+Q\sin (\phi ))=0\end{array}$

Mit etwas Übersicht können wir die drei Gleichungen stark vereinfachen, wenn wir die dritte Gleichung nach $x$ ableiten und die ersten beiden Gleichungen nutzen, um Terme zu eliminieren:

$\begin{array}{l}\frac{d^2}{d{x}^2}\left(M\right)+\underset{=0\text{ wg. Gleichung 2 oben}}{\underbrace{\frac{d}{dx}(N\sin (\phi )+Q\cos (\phi ))}}+\frac{d^2}{d{x}^2}w(-N\cos (\phi )+Q\sin (\phi ))+\frac{d}{dx}w\underset{=0\text{ wg. Gleichung 1 oben}}{\underbrace{\frac{d}{dx}(-N\cos (\phi )+Q\sin (\phi ))}}=0\end{array}$

Differentialgleichung der Biegelinie für den Knickfall

Wir gehen weiter davon aus, dass wir in dieser Gleichung $|Q\sin (\phi )|\ll |N\cos (\phi )|$ und $-N\cos (\phi )\approx P$ setzen dürfen - die Querkraft wird klein gegenüber der Normalkräft sein, und die Normalkraft setzen wir zur äußeren, eingeprägten Druckkraft $P$.

Dann erfasst die Differentialbeziehung

$M^{″}+P\cdot w^{″}=0$

das Knickproblem. Für den Euler-Bernoulli-Balken mit konstanter Querschnittsfläche gilt demnach für die Auslenkung $w(x)$ die Gleichgewichtsbedingung

$EI{w}^{IV}+P\cdot w^{″}=0.$

Diese lineare Differentialgleichung liefer mit dem Ansatz $w(x)=e^{\kappa x}$ die vier Eigenwerte

$\begin{array}{lll}{\kappa }_1& =& 0,\\ {\kappa }_2& =& 0,\\ {\kappa }_3& =& +j\cdot \sqrt{\frac{P}{EI}},\\ {\kappa }_4& =& -j\cdot \sqrt{\frac{P}{EI}},\\ \end{array}$

wobei $j:=\sqrt{-1}$. Die Lösung der Differentialbeziehung ist demnach mit $\kappa :={\kappa }_3$

$w(x)=W_1+W_2\cdot x+W_3\cdot \sin (\kappa x)+W_4\cdot \cos (\kappa x)$,

die $W_1,W_2,W_3,W_4$ sind reellwertige Integrationskonstanten, die aus den Randbedingungen des Problems kommen.

Beispiel: erster Eulerscher Knickfall

Für den ersten Eulerschen Knickfall oben gilt

$\begin{array}{lll}w(0)& =& 0\\ w^{\prime }(0)& =& 0\\ -EI{w}^{″}(\ell )& =& 0\\ -EI{w}^{‴}(\ell )-P{w}^{\prime }(\ell )& =& 0,\\ \end{array}$

also in Matrixschreibweise

$\underset{\underset{\_}{\underset{\_}{A}}}{\underbrace{\left(\begin{array}{cccc}1& 0& 0& 1\\ 0& 1& \kappa & 0\\ 0& 0& {\kappa }^{2}EI\sin (\kappa \ell )& {\kappa }^{2}EI\cos (\kappa \ell )\\ 0& -{\kappa }^{2}EI& 0& 0\\ \end{array}\right)}}\cdot \left(\begin{array}{c}{W}_1\\ W_2\\ W_3\\ W_4\\ \end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ \end{array}\right)$

Dieses homogene Gleichungssystem hat nichttriviale - von Null verschiedene - Lösungen, wenn

$\text{det}(\underset{\_}{\underset{\_}{A}})={\kappa }^5\cos (\kappa \ell )\stackrel{!}{=}0$

ist, also

${\kappa }_0=0,{\kappa }_1\ell =\pm \frac{\pi }{2},{\kappa }_2\ell =\pm \frac{3\pi }{2},\dots$.

Der kritische Wert von $\kappa$ ist der niedrigeste, zur nicht-trivialen Lösung gehörende Wert ${\kappa }_1$ und damit

$P_{krit}=\frac{{\pi }^{2}EI}{4{\ell }^2}$.

Das gezeigte Vorgehen finden Sie in allen Mechanik-Lehrbüchern. Der Lösungsansatz "Gleichgewicht am ausgelenkten System" funktioniert allerdings nur gut für sehr einfache Systeme. Für technsche relevante Systeme brauchen wir einen Ansatz, der immer funktionert und bei dem man kein Freikörperbild zeichnen muss. Das geht mit dem Prinzip der virtuellen Verrückungen.

Ansatz mit dem Prinzip der virtuellen Verrückungen mit großen Dehnungen

Für den Einsatz in Finite-Elemente-Methoden ist der Ansatz über ein Kräftegleichgewicht wie oben nicht möglich und sinnvoll: im Allgemeinen kann man für die zu untersuchenden Systeme kein Kräftegleichgewicht aufstellen. Hier geht man vom Prinzip der virtuellen Verrückungen aus, wobei in der virtuellen Formänderungsarbeit

$\delta \mathrm{\Pi }=\underset{V}{\int }\underset{\_}{\sigma }\cdot \delta \underset{\_}{\epsilon }dV$

die Dehnung $\underset{\_}{\epsilon }$ nichtlineare Anteile der Koordinaten der Verformung enthält. Nach unserer Untersuchung oben erwarten wir dabei nichtlineare Terme in den Koordianten, also mindestens Anteile mit $u^{\prime }(x)\cdot w^{″}(x)$, bei dem die Längskraft (hier $u^{\prime }$) in Kombination mit der Biegung (hier $w^{″}$) auftritt.

Wir müssen also in $\delta \mathrm{\Pi }$ nichtlineare Anteile mitnehmen.

Kinematik der Bewegung der materiellen Punkte

Wir konstruieren die Auslenkung des Punktes $P$ mit den unabhängigen, materiellen Koordinaten $x,y,z$ und den abhängigen Koordinaten $u(x),w(x),\phi (x)$:

Kinemtik der Auslenkung eines Stab-Querschnitts $x$.

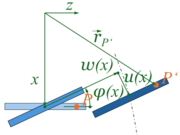
Aus dem Bild lesen wir die als Ortsvektor (die Koeffizienten des Ortsvektors) zum Punkt $P^{\prime }$ ab:

${\underset{\_}{r}}_{P^{\prime }}=\left(\begin{array}{c}x\\ 0\\ 0\\ \end{array}\right)+\underset{\_}{\underset{\_}{D}}(\phi (x))\cdot \left(\begin{array}{c}u(x)\\ y\\ w(x)+z\\ \end{array}\right)$

mit der Eulerschen Drehmatrix

$\underset{\_}{\underset{\_}{D}}(\phi )=\left(\begin{array}{ccc}\cos (\phi )& 0& \sin (\phi )\\ 0& 1& 0\\ -\sin (\phi )& 0& \cos (\phi )\end{array}\right)$.

Wir erhalten für die Auslenkung des Punktes P demnach

$\begin{array}{lll}\mathrm{\Delta }{\underset{\_}{r}}_P& =& {\underset{\_}{r}}_{P^{\prime }}-{\underset{\_}{r}}_P\\ & =& \left(\begin{array}{c}u\cos (\phi )-\sin (\phi )(z+w)\\ 0\\ \cos (\phi )(z+w)-z+u\sin (\phi )]\end{array}\right)\end{array}$

Uns interessiert hier nur der ebene Spannungszustand in der $x-z$-Ebene, bei dem außerdem noch ${\sigma }_{zz}=0$ ist. Mit den allgemeinen Beziehungen in der Ebene für den Zusammenhang zwischen den Auslenkungen $u_i$ und den materiellen Koordinaten $x_j$

${\epsilon }_{i,j}=\frac{1}{2}(\frac{\partial u_i}{x_j}+\frac{\partial u_j}{x_i})$

erhalten wir hier

$\underset{\_}{\epsilon }=\left(\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{zz}\\ {\epsilon }_{xz}\\ \end{array}\right)=\left(\begin{array}{c}-(\cos (\phi ){\phi }^{\prime }(z+w))-u\sin (\phi ){\phi }^{\prime }-w^{\prime }\sin (\phi )+u^{\prime }\cos (\phi )\\ \cos (\phi )-1\\ -(\sin (\phi ){\phi }^{\prime }(z+w))+u\cos (\phi ){\phi }^{\prime }+u^{\prime }\sin (\phi )-\sin (\phi )+w^{\prime }\cos (\phi )\end{array}\right)$

Die Spannungen $\underset{\_}{\sigma }$ kommen dann - mit der Annahme ${\sigma }_{zz}=0$, dem Elastizitätsmodul $E$ und dem Schubmodul $G$ - aus

$\underset{\_}{\sigma }=\left(\begin{array}{ccc}E& 0& 0\\ 0& 0& 0\\ 0& 0& G\end{array}\right)\cdot \left(\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{zz}\\ {\epsilon }_{xz}\\ \end{array}\right)$.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 21.05.3                           */
/* author: Andreas Baumgart                            */
/* last updated: 2025-11-20                            */
/* ref: buckling of straight rods                      */
/*      FEM-formulation (large strain analysis)        */
/*******************************************************/
/* parameters*/
assume(d>0, e>0, ℓ[e]>0);
params: [ℓ[e]=100*d,A=d^2, I=%pi*d^4/64, G=E/(2*(1-ν)), ν=0.3];

/* trial functions */
ψ: [[1-ξ,ξ],
    [2*ξ^3-3*ξ^2+1,
     ℓ[e]*ξ^3-2*ℓ[e]*ξ^2+ℓ[e]*ξ,
     3*ξ^2-2*ξ^3,
     ℓ[e]*ξ^3-ℓ[e]*ξ^2]];
/* coordinates and their variations */
Q :[[ U[e-1], U[e]],[ W[e-1], Φ[e-1], W[e], Φ[e]],
    [δU[e-1],δU[e]],[δW[e-1],δΦ[e-1],δW[e],δΦ[e]]];

dimless: [ξ=x/ℓ[e]];

trials: [ u(x)= sum(Q[1][i]*ψ[1][i],i,1,2),
         δu(x)= sum(Q[3][i]*ψ[1][i],i,1,2),
          w(x)= sum(Q[2][i]*ψ[2][i],i,1,4),
         δw(x)= sum(Q[4][i]*ψ[2][i],i,1,4)];

/* linear stre-strain-relations (not employed) */
k: E/(1-ν^2)*matrix([1,ν,0],[ν,1,0],[0,0,1-ν]);

/* functional coordinates and their variations */
coord: [[u(x),w(x),φ(x)],[δu(x),δw(x),δφ(x)]];
/* compute strains and their vaiations*/
null : makelist(coord[1][i]=0,i,1,3);
disp: r(x,y,z) = [x,0,0]+[[cos(φ(x)),0,sin(φ(x))],[0,1,0],[-sin(φ(x)),0,cos(φ(x))]].[u(x),y,w(x)+z];
disp: [disp, Δr(x,y,z) = subst(disp,r(x,y,z))-subst(null,subst(disp,r(x,y,z)))];

ε : [diff(subst(disp,Δr(x,y,z))[1],x),
     diff(subst(disp,Δr(x,y,z))[3],z),
     1/2*(diff(subst(disp,Δr(x,y,z))[1],z)+diff(subst(disp,Δr(x,y,z))[3],x))];
ε : expand(ε);

δε : subst(η=0,sum(diff(subst([coord[1][i] = coord[1][i]+η*coord[2][i]],ε),η),i,1,3));

/* compute stresses σ assuming σ[yy]=0 */
σ : [E*ε[1],0,G*ε[3]];

Virtuelle Arbeiten am Stabelement

Wie üblich bei der Methode der Finiten Elemente setzen wir die Arbeitsanteile additiv aus den Element-Arbeiten zusammen, also auch für die virtuelle FOrmänderungsarbeit

$\delta \mathrm{\Pi }=\sum _e\delta {\mathrm{\Pi }}_e.$

Für $\delta {\mathrm{\Pi }}_e$ im Element benötigen wir noch - wie im Lexikon-Eintrag "virtuelle Verrückung" beschreiben - die virtuelle Dehnung $\delta \underset{\_}{ϵ}$. Daraus folgt die virtuelle Formänderungsarbeit zu

$\delta \mathrm{\Pi }=\underset{V}{\int }(G\delta \phi \cos (\phi )\sin (\phi )\phi {\text{'}}^2{z}^2)/4-E\delta \phi \cos (\phi )\sin (\phi )\phi {\text{'}}^2{z}^2+(G\delta {\phi }^{\prime }\sin (\phi {)}^2{\phi }^{\prime }{z}^2)/4+E\delta {\phi }^{\prime }\cos (\phi {)}^2{\phi }^{\prime }{z}^2+(Gu\delta \phi \sin (\phi {)}^2\phi {\text{'}}^{2}z)/4-Eu\delta \phi \sin (\phi {)}^2\phi {\text{'}}^{2}z+\dots \text{ viele weitere Terme }dV$

in der insgesamt 121 Summanden stehen. Die Integration über die Querschnittsfläche liefert hier

$\delta {\mathrm{\Pi }}_e=\underset{{\ell }_e}{\int }(\underset{=(\dots )A}{\underbrace{\underset{A}{\int }(\dots )\cdot 1dA}}+\underset{=0}{\underbrace{\underset{A}{\int }(\dots )\cdot zdA}}+\underset{=(\dots )I}{\underbrace{\underset{A}{\int }(\dots )\cdot z^{2}dA}})dx$.

Die Komplexität dieses Ausdrucks ist erhelblich und eine genauere Untersuchung der einzelnen Terme nicht zielführend. Wir suchen nach zweckmäßigen Vereinfachungen und setzen zunächst

$\cos (\phi )=1$ und $\sin (\phi )=\phi$.

Dann vernachlässign wir alle Summenden, in denen mehr als zwei funktionalen Freiheitsgrade auftrauchen, also z.B. Terme mit $w{\phi }^2{u}^{\prime }$. Dann bleibt

$\delta {\mathrm{\Pi }}_e=EI\delta {\phi }^{\prime }{\phi }^{\prime }+(AGu(x)\delta w^{\prime }{\phi }^{\prime })/4-AEw(x)\delta u^{\prime }{\phi }^{\prime }+(AG\delta u(x)w^{\prime }{\phi }^{\prime })/4-AE\delta w(x)u^{\prime }{\phi }^{\prime }-(AG\delta u(x)\phi {\phi }^{\prime })/4-(AGu(x)\delta \phi {\phi }^{\prime })/4+(AGu(x)w^{\prime }\delta {\phi }^{\prime })/4-AEw(x)u^{\prime }\delta {\phi }^{\prime }-(AGu(x)\phi \delta {\phi }^{\prime })/4+(AG{w}^{\prime }\delta w^{\prime })/4+(AG\phi u^{\prime }\delta w^{\prime })/4-AE\phi u^{\prime }\delta w^{\prime }-(AG\phi \delta w^{\prime })/4+(AG\phi w^{\prime }\delta u^{\prime })/4-AE\phi w^{\prime }\delta u^{\prime }+AE{u}^{\prime }\delta u^{\prime }-(AG{\phi }^2\delta u^{\prime })/4+(AG\delta \phi u^{\prime }{w}^{\prime })/4-AE\delta \phi u^{\prime }{w}^{\prime }-(AG\delta \phi w^{\prime })/4-(AG\delta \phi \phi u^{\prime })/2+(AG\delta \phi \phi )/4$

- ein Ausdruck mit nur noch 23 Summenden. Hier wählen wir noch die Euler-Bernoulli-Hypothese

$\phi (x)=w^{\prime }(x)$ sowie $\delta \phi (x)=\delta w^{\prime }(x)$

und setzen nun unsere aus der Methode der FEM bekannten Ansatzfunktionen

$\begin{array}{lll}u(x)& =& U_{e-1}\cdot (1-\xi )+U_e\cdot (\xi )\\ w(x)& =& W_{e-1}\cdot (2{\xi }^3-3{\xi }^2+1)+{\mathrm{\Phi }}_{e-1}\cdot ({\xi }^3-2{\xi }^2+\xi ){\ell }_e+W_e\cdot (3{\xi }^2-2{\xi }^3)+{\mathrm{\Phi }}_e\cdot ({\xi }^3-{\xi }^2){\ell }_e\end{array}$

Das geschieht analog für $\delta u(x),\delta w(x)$ in $\delta {\mathrm{\Pi }}_e$. Dann führen wir die Integration über die Stablänge in $x=\xi {\ell }_e$aus.

Wir berücksichtigen als äußere, eingeprägte Lasten im Element eine konstante Streckenlast $q_0$ senkrecht zur Stab-Längsachse. Für diese Lastform auf den Stab nehmen wir die Ergebnisse aus den Faltungsintegralen für kubische Formfunktionen

$\delta W_e^a=q_0{\ell }_e(+\frac{1}{2}\delta W_{e-1}-\frac{{\ell }_e}{12}\delta {\mathrm{\Phi }}_{e-1}+\frac{1}{2}\delta W_e+\frac{{\ell }_e}{12}\delta {\mathrm{\Phi }}_e)$

hinzu, so dass wir die virtuelle Arbeit $\delta W_e$ je Element zu

$\delta {\mathrm{\Pi }}_e=(\delta U_{e-1},\delta U_e,\delta W_{e-1},\delta {\mathrm{\Phi }}_{e-1},\delta W_e,\delta {\mathrm{\Phi }}_e)\cdot \left(\begin{array}{c}-\left(\frac{AE{W}_e{\mathrm{\Phi }}_e}{{\ell }_e}\right)+\frac{AE{U}_e}{{\ell }_e}+\frac{AE{W}_{e-1}{\mathrm{\Phi }}_{e-1}}{{\ell }_e}-\frac{AE{U}_{e-1}}{{\ell }_e}\\ \frac{AE{W}_e{\mathrm{\Phi }}_e}{{\ell }_e}-\frac{AE{U}_e}{{\ell }_e}-\frac{AE{W}_{e-1}{\mathrm{\Phi }}_{e-1}}{{\ell }_e}+\frac{AE{U}_{e-1}}{{\ell }_e}\\ \frac{q_0{\ell }_e}{2}-\frac{AE{\mathrm{\Phi }}_{e-1}{U}_e}{{\ell }_e}+\frac{AE{U}_{e-1}{\mathrm{\Phi }}_{e-1}}{{\ell }_e}-\frac{6EI{\mathrm{\Phi }}_e}{{\ell }_e^2}-\frac{6EI{\mathrm{\Phi }}_{e-1}}{{\ell }_e^2}+\frac{12EI{W}_e}{{\ell }_e^3}-\frac{12EI{W}_{e-1}}{{\ell }_e^3}\\ \frac{q_0{\ell }_e^2}{12}-\frac{2EI{\mathrm{\Phi }}_e}{{\ell }_e}-\frac{AE{W}_{e-1}{U}_e}{{\ell }_e}-\frac{4EI{\mathrm{\Phi }}_{e-1}}{{\ell }_e}+\frac{AE{U}_{e-1}{W}_{e-1}}{{\ell }_e}+\frac{6EI{W}_e}{{\ell }_e^2}-\frac{6EI{W}_{e-1}}{{\ell }_e^2}\\ \frac{q_0{\ell }_e}{2}+\frac{AE{U}_e{\mathrm{\Phi }}_e}{{\ell }_e}-\frac{AE{U}_{e-1}{\mathrm{\Phi }}_e}{{\ell }_e}+\frac{6EI{\mathrm{\Phi }}_e}{{\ell }_e^2}+\frac{6EI{\mathrm{\Phi }}_{e-1}}{{\ell }_e^2}-\frac{12EI{W}_e}{{\ell }_e^3}+\frac{12EI{W}_{e-1}}{{\ell }_e^3}\\ -\left(\frac{q_0{\ell }_e^2}{12}\right)-\frac{4EI{\mathrm{\Phi }}_e}{{\ell }_e}+\frac{AE{U}_e{W}_e}{{\ell }_e}-\frac{AE{U}_{e-1}{W}_e}{{\ell }_e}-\frac{2EI{\mathrm{\Phi }}_{e-1}}{{\ell }_e}+\frac{6EI{W}_e}{{\ell }_e^2}-\frac{6EI{W}_{e-1}}{{\ell }_e^2}\end{array}\right)$

finden.

/* virtuelle Formänderungsenergie */
δΠ: expand(σ.δε);
δΠ: makelist(coeff(δΠ,z,i),i,0,2);
δΠ: expand(A*δΠ[1] + I*δΠ[3]);
δΠ: expand(subst([cos(φ(x))=1,sin(φ(x))=φ(x)],δΠ));

/* controlled reduction of complexity -> throw out really very small contributions */
small: makelist(coord[1][i] = η*coord[1][i],i,1,3);
small: append(small, diff(small,x));
δΠ: expand(subst(small,δΠ));
δΠ: subst([η^6=0,η^5=0,η^4=0,η^3=0,η=1],ev(δΠ,nouns));

/* Euler-Bernoulli approach */
δΠ: subst([φ(x)=diff(w(x),x),δφ(x)=diff(δw(x),x)],δΠ);
δΠ: expand(ev(δΠ,nouns));

δΠ: subst(dimless,subst(trials,δΠ))$
δΠ: ev(δΠ,nouns)$
δΠ: expand(δΠ)$

/* integrate over length ℓ[e] */
δΠ: expand(integrate(expand(δΠ),x,0,ℓ[e]))$

δV[a]: expand(integrate(subst(dimless,subst(trials,q[0]*δw(x))),x,0,ℓ[e]))+P*δU[e-1];

equ : append( makelist(coeff(δV[a]-δΠ,Q[3][i]),i,1,2),
              makelist(coeff(δV[a]-δΠ,Q[4][i]),i,1,4))$

Beispiel: erster Eulerscher Knickfall

Für den Eulerschen Knickfall #1 wählen wir nun ein einziges Element, also $e=1$ und damit $\delta W=\delta W_e$ mit den Randbedingungen

$U_1=0,W_1=0\text{ und }{\mathrm{\Phi }}_1=0$.

Dann bringen wir eine vertiakle Drucklast $P$ auf den Stab mit $\delta W^a=P\delta U_0$ auf. Das resultierende Gleichungssystem in $\underset{\_}{Q}=(U_0,W_0,{\mathrm{\Phi }}_0)$

$\underset{\_}{f}(\underset{\_}{Q})=\underset{\_}{0}$

ist nichtlinear. Wir lösen es - nach weiteren Vereinfachungen - für die verbleibenden Koordinaten zu

$\begin{array}{ccc}{U}_0^{*}& =& \frac{P{\ell }_e}{AE}\\ W_0^{*}& =& -\left(\frac{q_{0}P{\ell }_e^6+18q_{0}EI{\ell }_e^4}{12P^2{\ell }_e^4-144EIP{\ell }_e^2-144E^2{I}^2}\right)\\ {\mathrm{\Phi }}_0^{*}& =& -\left(\frac{q_{0}P{\ell }_e^5-4q_{0}EI{\ell }_e^3}{2P^2{\ell }_e^4-24EIP{\ell }_e^2-24E^2{I}^2}\right)\end{array}$.

Um den Knickfall zu bestimmen, "wackeln" wir an dieser statischen Lösung mit $P=P+\mathrm{\Delta }P$ und suchen nach Lösungen

$\begin{array}{ccc}{U}_0& =& U_0^{*}+\mathrm{\Delta }{U}_0\\ W_0& =& W_0^{*}+\mathrm{\Delta }{W}_0\\ {\mathrm{\Phi }}_0& =& {\mathrm{\Phi }}_0^{*}+\mathrm{\Delta }{\mathrm{\Phi }}_0\end{array}$,

schauen also nach der Lösung für

$\underset{\_}{f}({\underset{\_}{Q}}^{*}+\mathrm{\Delta }\underset{\_}{Q})=\underset{\_}{0}$

Wir approximieren dies für kleine $\mathrm{\Delta }\underset{\_}{Q}$ zu

$\underset{\_}{f}({\underset{\_}{Q}}^{*})+{\frac{\partial \underset{\_}{f}}{\partial \mathrm{\Delta }\underset{\_}{Q}}|}_{{\underset{\_}{Q}}^{*}}\cdot \mathrm{\Delta }\underset{\_}{Q}={\underset{\_}{f}}^{*}(\mathrm{\Delta }\underset{\_}{P})$

Dies führt - wegen $\underset{\_}{f}({\underset{\_}{Q}}^{*})=\underset{\_}{0}$ - auf das lineare Gleichungssystem

$\underset{\underset{\_}{\underset{\_}{A}}}{\underbrace{\left(\begin{array}{ccc}-\left(\frac{AE}{{\ell }_e}\right)& 0& 0\\ -\left(\frac{q_{0}AEP{\ell }_e^4-4q_{0}A{E}^{2}I{\ell }_e^2}{2P^2{\ell }_e^4-24EIP{\ell }_e^2-24E^2{I}^2}\right)& -\left(\frac{12EI}{{\ell }_e^3}\right)& \frac{P{\ell }_e^2-6EI}{{\ell }_e^2}\\ -\left(\frac{q_{0}AEP{\ell }_e^5+18q_{0}A{E}^{2}I{\ell }_e^3}{12P^2{\ell }_e^4-144EIP{\ell }_e^2-144E^2{I}^2}\right)& \frac{P{\ell }_e^2-6EI}{{\ell }_e^2}& -\left(\frac{4EI}{{\ell }_e}\right)\end{array}\right)}}\cdot \mathrm{\Delta }\underset{\_}{Q}={\underset{\_}{f}}^{*}(\mathrm{\Delta }\underset{\_}{P})$

Knicken tritt dann ein, wenn es im Umfeld von ${\underset{\_}{Q}}^{*}$ keine Lösung für $\mathrm{\Delta }\underset{\_}{Q}$ gibt, also

$\begin{array}{ccc}\text{det}(\underset{\_}{\underset{\_}{A}})& =& 0\\ & =& \frac{AE{P}^2}{{\ell }_e}-\frac{12A{E}^{2}IP}{{\ell }_e^3}-\frac{12A{E}^3{I}^2}{{\ell }_e^5}\end{array}$

Das ist für

$P=\frac{(4\sqrt{3}\mathrm{+}6)EI}{{\ell }_e^2}$

der Fall. Der Vergleich der analytischen Lösung oben mit unserer Näherungslösung basierend auf einem Finiten Element liefert:

$P_{krit.}=\frac{12.9EI}{{\ell }_e^2},P_{FEM}=\frac{9.9EI}{{\ell }_e^2}$

Das FE-Modell liefert also eine deutlich geringere kritische Knicklast, als die analytische Lösung. Ob dies beim Einsatz von mehr Finiten Elementen für eine Untersuchung besser wird, kann in Modellen mit mehr Finiten Elemente untersucht werden.

Durch den Einsatz des Prinzips der virtuellen Verrückungen haben wir ein numerisches Näherungsverfahren, mit dem wir praktisch beliebig komplizierte Systeme untersuchen können. Aufwändig ist dabei jeweils die Lösung des nichtlinearen Gleichungssystems

$\underset{\_}{f}(\underset{\_}{Q})=\underset{\_}{0}$,

das Finden der Knick-Eigenwerte "P" des Systems ist dann numerisch relativ einfach.

/* test with only one Finite Element and for Euler-case "1" */
/* boundary condictions: U[e]=0, Φ[e]=0, W[e]=0 */
minCoords: [U[e-1],W[e-1],Φ[e-1]];
bc: [U[e]=0, W[e]=0, Φ[e]=0];
equ : subst(bc,[equ[1],equ[3],equ[4]])$
equ[1]: subst([Φ[e-1]=0,Φ[e]=0],equ[1]);
sol: solve(equ,minCoords)[1];

/* Linearization about this solution */
minCoords: [minCoords, [ΔU[e-1],ΔΦ[e-1],ΔΦ[e]]];
null: makelist(minCoords[2][i]=0,i,1,3);

Δequ: expand(subst(sol,subst([P=P+ΔP,q[0]=q[0]+Δq[0]],subst(makelist(minCoords[1][i]=minCoords[1][i]+minCoords[2][i],i,1,3),equ))));
Δequ: expand(ratsimp(Δequ));
Δequ: subst(null,Δequ) + sum(subst(null,diff(Δequ,minCoords[2][i]))*minCoords[2][i],i,1,3);

ACM: augcoefmatrix(Δequ, minCoords[2]);
K: submatrix(ACM,4);
p: -col(ACM,4);

/* we are interested to find P so that no more solution is feasable -> det(K) = 0 */
knicken: ratsimp(solve(determinant(K),P)[2]);

/* compare */
EulerKnickfall:[P=(%pi/2)^2*E*I/ℓ[e]^2,P=%pi^2*e*I/ℓ[e]^2]; 

print(knicken," : ", EulerKnickfall[2])$;
print(float(knicken)," : ", float(EulerKnickfall[2]))$;
print(expand(float(subst(params,knicken)))," : ", float(subst(params,EulerKnickfall[2])))$;

---

Links

• ...

Literature

• ...