Sources/Anleitungen/Die Prinzipien der Mechanik

Dies ist ein Auszug aus dem Buch

• Szabó, István: Höhere Technische Mechanik, 8. Aufl., Berlin/Heidelberg: Springer 2001

Die Prinzipien der Mechanik

In diesem Kapitel wird ein einheitlicher Aufbau der gesamten Mechanik gegeben. Dazu werden wir von zwei Axiomen ausgehen, die wir Prinzipien nennen werden. Es wurde schon in der "Einführung in die Technische Mechanik" (Szabó, István: Einführung in die Technische Mechanik, 8. Aufl., Berlin/Heidelberg/New York: Springer 1975, im folgenden als "Einführung" zitiert.) darauf hingewiesen, dass an eine solohe Systematik zweckmaßigerweise erst nach Durchschreiten des historischen Weges gedacht werden sollte, d.h., nachdem die Statik und Dynamik des starren Korpers und die einfachsten Gesetze der festen elastischen Körper aus einigen durch die Erfahrung eingegebenen Axiomen aufgebaut worden sind. Diese Inspiration durch die Erfahrung zu betonen, ist notwendig, denn die oben erwahnten zwei Prinzipien, namlich das der virtueUen Arbeiten und das von d'Alembert, werden uns auf den ersten Blick weder anschaulich notwendig erscheinen, wie etwa die Axiome der Euklidischen Geometrie, noch werden sie durch die Erfahrung eingegeben, wie z. B. die Gleichgewichtsbedingungen fur die Kräfte am starren Körper.

Blicken wir noch einmal auf den Aufbau der Mechanik in der "Einführung" zuruck: Wir begannen mit der Statik des starren Körpers, und nach Einführung der Axiome von der Linienflüchtigkeit des Kraftvektors und vom Kräfteparallelogramm sprachen wir die Gleichgewichtsbedingung am starren Körper (ebenfalls als Axiom) in der Form

$\sum _{j=1}^n{\overrightarrow{F}}_j^a=\overrightarrow{0}$ und $\sum _{j=1}^n{\overrightarrow{r}}_j\times {\overrightarrow{F}}_j^a=\overrightarrow{0}$ (*)

aus. Hierbei bedeuten ${\overrightarrow{F}}_j^a$ die äußeren Kräfte, d.h. die eingeprägten und die Reaktionskräfte. Aus den aus (*) hervorgehenden 6 Komponentengleichungen konnten im allgemeinen ebenso viele unbekannte Reaktionslastkomponenten ermittelt werden (statisch bestimmtes Problem). Bei mehr Unbekannten muBten die Fiktion des starren Korpers aufgegeben und das elastische Verhalten des Materials berücksichtigt werden (statisch unbestimmte Probleme). Vollig unabhangig von der Statik, wenn auch unter Heranziehung des statischen Kraftbegriffes, wurden anknüpfend an das Neunoneche Gesetz ("Einfuhrung" §2Q Ziff. 1 und 2) die beiden grundlegenden Gesetze der Dynamik (Schwerpunkt und Momentensatz) hergeleitet ("Einführung" §20 Ziff. 3 und 4). Damit begann man jedoch schon die Grenzen der Newtonschen Mechanik zu überschreiten, denn diese wurde eigentlich aus dem Studium der Planetenbewegung heraus, d. h. fur die freie Bewegung eines "Massenpunktes", aufgebaut. Bei den irdischen Bewegungen - und das ist die eigentliche Aufgabe der Technischen Mechanik - hat man es aber im allgemeinen aber mit Massenpunkten noch mit freien Bewegungen, sondern mit gebundenen Bewegungen eines räumlich ausgedehnten Körpers bzw. Körpersystems zu tun, und hier erweist sich die Newtonsche "Mechanik des Massenpunktes" als zu eng. Die Erweiterung des Newtonschen Grundgesetzes auf das Massenelement bedeutet den ersten entscheidenden Schritt zu einem einheitlichen Aufbau der gesamten Mechanik, mit dem die Namen Euler (1707-1783), d'Alembert (1717-1783) und Lagrange (1736-1813) unlöslich verbunden sind. Die von den letzteren ausgesprochenen Gesetze (Prinzipien) finden - im Gegensatz zum Newtonschen Gesetz- auf der Statik, und sie treffen in deren Sinne die gesamte Mechanik umfassende Aussagen als Gleichgewichtsprinzipien. Dementsprechend beginnen wir mit dem Aufbau einer starre- und deformierbare Körper umfassenden Statik.

Das Prinzip der virtuellen Arbeiten als allgemeines Grundgesetz der Statik

Einleitende Bemerkungen und der Begriff der virtuellen Verrückung

Die Kopplung des Prinzips mit dem Arbeitsbegriff bringt schon zum Ausdruck, daß man auch in der Statik, wie in der Physik durch das Prinzip der Erhaltung der Energie [R. Meyer (1814-1878)], zu einem obersten einheitlichen Gesetz kommt, wenn man vom Energiebegriff, insbesondere von der bei einer Verschiebung geleisteten mechanischen Arbeit, ausgeht. Solche Bestrebungen und Versuche sind alt:

Schon bei Aristoteles (384-322 v. Chr.) - bei der Ableitung des Hebelgesetzes - finden sich solche Betrachtungen. Die erste, wenigstens in qualitativer Hinsicht richtige Aussage eines Energieprinzips stammt aus dem Mittelalter von Jordanus Nemorarius (um 1220).

Das Prinzip der virtuellen Arbeiten umfaßt das Prinzip der virtuellen Verrückungen und das Prinzip der virtuellen Kräfte. Mit dem erstgenannten ist der Begriff der virtuellen Verrückung aufs engste verknüpft. Unter einer virtuellen Verrückung oder Verschiebung $\delta \overrightarrow{r}$ verstehen wir eine

1. gedachte (also in Wirklichkeit nicht unbedingt eintretende),
2. differentiell kleine und
3. mit der geometrischen Konfiguration (Gestalt, Bindungen usw.)

vereinbare Verschiebung. Mit dem Parameter p schreiben wir

$\delta \overrightarrow{r}=\frac{\partial \overrightarrow{r}}{\partial p}\delta p$.

Das aus der Variationsrechnung entliehene Zeichen $\delta$ soll zum Ausdruck bringen, daß es sich um eine gedachte Verschiebung handelt, im Gegensatz zu einer wirklichen, die mit d bezeichnet und auch aktuelle Verschiebung genannt wird.

Zweischlag

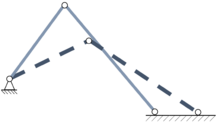
Bei dem in der Abbildung skizzierten Zweistabsystem ist eine einem (moglichen) Zustand gegenüber virtuell verschobene Lage, die man im Sinne der Variationsrechnung auch eine variierte nennt, gestrichelt angedeutet. Die virtuellen Verschiebungen sind also geometrisch und physikalisch mögliche Verschiebungen, die man sich zeitlos vorzustellen hat und die in Wirklichkeit nicht einzutreten brauchen. Selbstverstandlich gehören die wirklichen Verschiebungsdifferentiale bei von der Zeit unabhängigen Bindungen (skleronome Systeme) in die Klasse aller möglichen Verschiebungen!

🖌 skleronom - rheonom:

So ist z.B. ein gegen die Erde abgestütztes System skleronom, falls man die Erde als ruhend ansieht; sonst nicht skleronom (rheonom). Die Worte skleronom und rhemunn kommen aus dem Griechischen: skleronom = starres Gesetz; rheonom = fließendes Gesetz.

Bei einem System starrer Kerper lassen die virtuellen Verschiebungen die Gestalt der einzelnen Körper unverändert, während ein virtueller Verrückungszustand eines deformierbaren Körpers auch Körperverformungen zur Folge haben kann. Die differentielle Kleinheit der virtuellen Verrückungen setzen wir voraus, damit wir bei der Formulierung der virtuellen Arbeit die Kräfte als unabhängig von den variierten Verschiebungen ansehen konnen. Im Gegensatz hierzu werden beim Prinzip der virtuellen Krälte bei festgehaltenem Verschiebungszustand die Kräfte variiert; näheres hierzu siehe §2.4.

Das Prinzip der virtuellen Verrückungen für ein Körpersystem

Wir betrachten ein Volumenelement dV eines Systems, an dem die resultierende eingeprägte Kraft $d{\overrightarrow{F}}^e$ angreifen möge.

Volumenelement eines Körpers

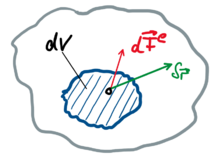
Bedeutet $\delta \overrightarrow{r}$ eine dem Kraftangriffspunkt von $d{\overrightarrow{F}}^e$ zugeordnete virtuelle Verschiebung, so ist die gesamte virtuelle Arbeit der eingepragten Kräfte am System

$\delta A^e=\underset{V}{\int }d{\overrightarrow{F}}^e\cdot \delta \overrightarrow{r}dV$

Greifen am System nur Einzelkräfte ${\overrightarrow{F}}_j^e$, (j = 1, 2, 3, ..., n) an, so hat man

$\delta A^e=\sum _{j=1}^n{\overrightarrow{F}}_j^e\cdot \delta {\overrightarrow{r}}_j$

Nun fordert das Prinzip der virtuellen Verrückungen als Axiom:

Ein mechanisches System befinde sich im Gleichgewicht, wenn die Gesamtarbeit der eingeprägten Krälte für jede mögliche virtuelle Verschiebung verschwindet:

$\delta A^e=0$.

Gemäß den obigen Gleichungen gilt also

$\delta A^e=\underset{V}{\int }d{\overrightarrow{F}}^e\cdot \delta \overrightarrow{r}dV=0$

bzw.

$\delta A^e=\sum _{j=1}^n{\overrightarrow{F}}_j^e\cdot \delta {\overrightarrow{r}}_j=0$

Im Gegensatz zu den bekannten Gleichgewichtsbedingungen am starren Korper ("Einführung" §7.3) erscheint das Prinzip der virtuellen Verrückungen keinesfalls evident, wenn es auch - nach einigem Überlegen, einer anschaulichen Deutung fähig ist: Die angreifenden Kräfte zeigen keine Tendenz, das System durch Arbeitsleistung in Bewegung zu setzen.

Damit ist freilich nichts bewiesen, und eines solchen Beweises ist das Prinzip der virtuellen Verrücknngen als Axiom weder fähig noch bedürftig: Es muB seine nachtragliche Rechtfertigung in der Übereinstimmung mit der Erfahrung finden, und das ist der Fall. Das Prinzip der virtuellen Verrückungen wird als ein für starre und deformierbare Systeme gültiges Axiom postuliert; im ersten Falle (starre Systeme) haben wir sofort die Möglichkeit, das Prinzip zu "erproben": Offenbar muß es auf die alten Gleichgewichtsbedingungen zurückführen. Für elastisch-deformierbare Systeme wird das Prinzip - wie wir später sehen werden - neben der Verifikation bekannter Ergebnisse neue Moglichkeiten fUr die Elastizitätstheorie eröffnen.

Bevor wir das Prinzip der virtuellen Verrückungen auf einen starren Körper bzw. auf ein System aus starren Körpern anwenden, noch eine grundsätzliche Bemerkung: In den obigen Gleichungen erscheinen nur die eingeprägten, nicht aber die Reaktionskräfte, obwohl gerade die Bestimmung der letzteren im Hinblick auf die zu erwartende Beanspruchung des Systems eine wesentliche Aufgabe der Statik ist! Hierzu ist folgendes zu sagen: Zunächst, ist es selbstverständlich, daß die Reaktionskräfte in der mathematischen Fassung des Prinzips nicht erscheinen können, da die Bindungen, in denen diese Kräfte wirken, unverschieblich sind, können von den Reaktionskräften auch keine Arbeiten geleistet werden. Die Möglichkeit, mit Hilfe des Prinzips der virtuellen Verrückungen die für das Gleichgewicht erforderlichen Reaktionakräfte zu ermitteln, liegt in dem sogenannten Befreiungsprinzip von Lagrange:

Man denke die starren (geometrischen) Bindungen durch nachgiebige (physikalische) ersetzt, wodurch aus den Reaktionskräften eingeprägte Kräfte werden, die nun mehr nach dem Prinzip der virtuellen Verrückungen ermittelt werden konnen. Diese Umwandlung ist der für uns wesentliche Inhalt des Befreiungsprinzips.

Nun zeigen wir, wie das Prinzip der virtuellen Verriickungen für den starren Körper bzw. für starre Systerne auf die wohlbekannten Gleichgewichtsbedingungen führt.

Zweischlag

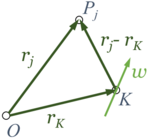
Zunächst sei an die Eulersche Formel ("Einführung" §19.7) erinnert, nach der eine differentiell kleine Verschiebung $\delta {\overrightarrow{r}}_j$ des Punktes $P_j$ eines starren Körpers sich zusammensetzen läßt aus der Translation $\delta {\overrightarrow{r}}_F$ eines körperfesten Punktes $F$ und aus einer Drehung um eine durch $F$ gehende Achse mit dem Einheitsvektor $\overrightarrow{w}$:

$\delta {\overrightarrow{r}}_j=\delta {\overrightarrow{r}}_F+\delta \phi \cdot \overrightarrow{w}\times ({\overrightarrow{r}}_j-{\overrightarrow{r}}_F)$.

Hierbei ist $\delta \phi$ die Winkeldrehung um die durch $\overrightarrow{w}$ festgelegte Achse. Damit liefert die Gleichung für die virtuelle Arbeit

$\delta A^e=(\delta {\overrightarrow{r}}_F-\delta \phi \cdot \overrightarrow{w}\times {\overrightarrow{r}}_F)\cdot \sum _{j=1}^n{\overrightarrow{F}}_j^e+\sum _{j=1}^n(\delta \phi \cdot \overrightarrow{w}\times {\overrightarrow{r}}_j)\cdot {\overrightarrow{F}}_j^e$

oder, wenn man im letzten Glied die für Kreuzprodukte gültige Regel

$(\overrightarrow{a}\times \overrightarrow{b})\cdot \overrightarrow{c}=\overrightarrow{a}\cdot (\overrightarrow{b}\times \overrightarrow{c})$

berücksichtigt,

$\begin{array}{lll}\delta A^e& =& (\delta {\overrightarrow{r}}_F-\delta \phi \cdot \overrightarrow{w}\times {\overrightarrow{r}}_F)\cdot {\overrightarrow{R}}^e+\delta \phi \cdot \overrightarrow{w}\sum _{j=1}^n{\overrightarrow{r}}_j\times {\overrightarrow{F}}_j^e\\ & =& (\delta {\overrightarrow{r}}_F-\delta \phi \cdot \overrightarrow{w}\times {\overrightarrow{r}}_F)\cdot {\overrightarrow{R}}^e+\delta \phi \cdot \overrightarrow{w}{\overrightarrow{M}}^e\end{array}$

wobei ${\overrightarrow{R}}^e$ die resultierende Kraft und ${\overrightarrow{M}}^e$ das auf den raumfesten Nullpunkt bezogene Moment aller eingeprägten Kräfte bedeuten. Für den freien starren Körper sind $\delta {\overrightarrow{r}}_F$ und $\delta \phi \overrightarrow{w}$ beliebige differentielle Änderungen, so daß aus obigen Gleichungen

${\overrightarrow{R}}^e=0,{\overrightarrow{M}}^e=0$

gefolgert werden können, während wir als Gleichgewichtsbedingungen in der Statik

${\overrightarrow{R}}^a=0,{\overrightarrow{M}}^a=0$

erhalten haben. Bei diesen letzten Gleichungen ist zu bedenken, daß die Einteilung der Kräfte in eingeprägte und Reaktianskräfte bzw. in innere und äußere Kräfte sich keinesfalls zu decken braucht: Es kann sowohl innere wie innere eingeprägte Kräfte als auch äußere und innere Reaktionskräfte geben; freilich brauchen sie nicht alle in einem System zugleich aufzutreten; so gibt es z.B. beim freien, starren Körper keine äußeren Reaktionskräfte und keine inneren eingeprägten Kräfte, so daß die Glecihungen identiseh werden; auch fur den gebundenen starren Körper ist dieses sofort einzusehen, wenn man bedenkt, daß nach dem Befreiungsprinzip die Reaktlonskräfte zu eingeprägten werden. Damit ist gezeigt, daß das Prinzip der virtuellen Verrückungen die früheren Gleichgewichtsbedingungen als Spezialfall enthält, aber es leistet noch weit mehr, wenn wir seine Gültigkeit, wie schon erwähnt, auch fur deformierbare Körper postulieren, bei denen im Zusammenhang mit einer virtuellen Verrückung auch gegenseitige (relative) Verschiebungen der Körperpunkte denkbar sind. In diesem Falle besagt das Prinzip, daß die Summe der virtuellen Arbeiten der äußeren eingeprägten Kräfte $\delta A_a^e$ und die der inneren $\delta A_i^e$ verschwindet:

$\delta A^e=\delta A_a^e+\delta A_i^e=0$.

Spezialisieren wir dieses Prinzip auf elastisch deformierbare Körper und bezeichnen die Arbeit, die der elastische Körper bei seiner Entspannung zu leisten vermag, mit $W$ bzw. $\delta W$, so ist offenbar $\delta A_i^e=-\delta W$, so daß mit $\delta A_a^e=\delta A$ die für elastische (dämpfungsfreie) Medien grundlegende Beziehung

$\delta A=\delta W$

hervorgeht.

Das ist aber der sog. "Energiesatz" : Die Arbeit der äußeren (eingeprägten) Kräfte bei einer virtuellen Verschiebung ist gleich dem Zuwachs der sog. Formänderungsarbeit $W$. Es muß hier besonders betont werden, daß $\delta A$ diejenige sog. "Endwert"-Arbeit der äußeren Kräfte ist, die diese leisten würden, wenn sie längs der virtuellen Verschiebungen mit ihren konstanten, dem Gleichgewichtszustand entsprechenden Werten wirken würden.

Fassen wir dagegen speziell die in der letzten Gleichung stehenden virtuellen Arbeiten als während einer - "unendlich langsamen!" - Verformung auftretende (aktuelle) Arbeitsdifferentiale auf, so können wir nach Integration über diese, wenn man vom spannungslosen Zustand ausgeht,

$\int dA=A_a=\int dW=W$

schreiben. Bei der zu $A_a$ führenden Integration ist natürlich die Abhängigkeit der Kräfte von den Deformationen zu berücksichtigen. $A_a$ bezeichnet man als äußere Formänderungsarbeit; das ist also die von den äußeren Kräften wirklich geleistete Arbeit,die mit der (Gesamt-)Endwertarbeit $A$, im Falle der Proportionalität zwischen äußeren Kräften und Verschiebungen, in der Beziehung

$2A_a=A$

steht.

Wir werden später sehen, daß das Prinzip der virtuellen Verrückungen, auf - im Sinne des Hooke'schen Gesetzes - elastische Körper angewandt, nicht nur von früher her bekannte Resultate liefert, sondern zu neuen Methoden und Erkenntnissen führt. Vorerst soll das Prinzip bei Gleichgewichtsproblemen starrer Körper "erprobt" werden. Zur praktischen Durchführung solcher Aufgaben ist grundsätzlich folgendes zu sagen:

Man wähle ein von den möglichen Verschiebungen unabhängiges Koordinatensystem, bestimme in diesem System die zu den Kraftangriffspunkten führenden Radiusvektoren ${\overrightarrow{r}}_j$ und bilde ihre virtuellen Verschiebungen $\delta {\overrightarrow{r}}_j$ - nach den Regeln der Analysis- als Differentiale, wodurch die Bildung der virtuellen Arbeit der eingeprägten bzw. der nach dem Befreiungaprinzip zu eingeprägten gewordenen Reaktionakräfte möglich ist. Dann sucht man- entsprechend der geometriachen Konfiguration des Systems Beziehungen zwischen den virtuellen Verschiebungen, so daß in dem Ausdruck für die virtuellen Arbeiten genauso viele voneinander unabhängige Verschiebungen $\delta {\overrightarrow{r}}_j$ übrigbleiben, wie das Syatem Freiheitsgrade hat; man kann nun - wegen der Willkürlichkeit dieser Verschiebungen $\delta {\overrightarrow{r}}_j$ fordern, daß ihre Koeffizienten für sich verschwinden müssen, und das liefert die gesuchten Gleichgewichtsbedingungen des Systems.

Beispiele und Anwendungen

Die doppelschiefe Ebene

Zwei auf je einer schiefen Ebene verschiebbare Körper $G_1$ und $G_2$ sind mit einem uber eine Rolle geführten Faden von der Länge $\ell ={\ell }_1+{\ell }_2+{\ell }_R$ verbunden.

Körper auf doppelschiefer Ebene

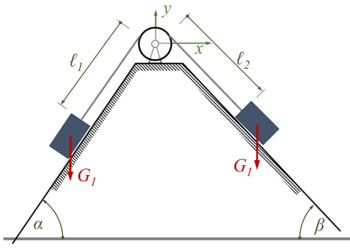
Man ermittle die Bedingung fur das Gleichgewicht. Sehen wir von der Reibung ab, so hat man in dem gezeichneten Koordinatensystem

${\underset{\_}{F}}_1^e=\left(\begin{array}{c}0\\ G_1\\ 0\end{array}\right),{\underset{\_}{F}}_2^e=\left(\begin{array}{c}0\\ G_2\\ 0\end{array}\right),$

und, da das über den Rollenradius liegende Seillänge als konstant anzusehen ist,

${\underset{\_}{r}}_1={\ell }_1\cdot \left(\begin{array}{c}-\cos (\alpha )\\ -\sin (\alpha )\\ 0\end{array}\right),{\underset{\_}{r}}_2={\ell }_2\cdot \left(\begin{array}{c}+\cos (\beta )\\ -\sin (\beta )\\ 0\end{array}\right)$

und damit

$\delta {\underset{\_}{r}}_1=\delta {\ell }_1\cdot \left(\begin{array}{c}-\cos (\alpha )\\ -\sin (\alpha )\\ 0\end{array}\right),{\underset{\_}{r}}_2=\delta {\ell }_2\cdot \left(\begin{array}{c}+\cos (\beta )\\ -\sin (\beta )\\ 0\end{array}\right)$

Die virtuelle Arbeit beträgt nun

$\delta A^e={\underset{\_}{F}}_1\cdot \delta {\underset{\_}{r}}_1+{\underset{\_}{F}}_2\cdot \delta {\underset{\_}{r}}_2$

Nun ist (wegen ${\ell }_1+{\ell }_2=\ell -{\ell }_R=\text{const}$)

$\delta {\ell }_1+\delta {\ell }_2=0$

so daß schließlich aus

$\delta A^e=0=(G_1\sin \alpha -G_2\sin \beta )\cdot \delta {\ell }_1$

folgt.

Klappbrücke

Kein Inhalt.

Zugbrücke

Kein Inhalt.

Das Torricellische Prinzip

Kein Inhalt.

Die Arten des Gleichgewichtes
- stabiles und labiles Gleichgewicht -

Knoten eines allgemeinen Fachwerks.

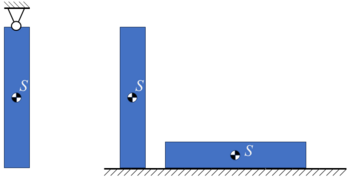
Jeder weiß aus der Erfahrung, dass es verschiedene Arten des Gleichgewichtes gibt, und verbindet mit den Worten "stabiles, labiles und indifferentes Gleichgewicht" eine bestimmte, meistens dem Kraftfeld der Schwere entnommene Vorstellung. So weiß jeder, daß ein Stab sich im stabilen, labilen oder indifferenten Gleichgewicht befindet, je nachdem, ob er oberhalb, unterhalb oder in seinem Schwerpunkt aufgehängt, bzw. unterstützt wird.

Knoten eines allgemeinen Fachwerks.

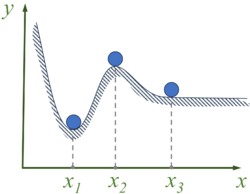
Ein anderes sehr instruktives Beispiel ist eine kleine Kugel, die auf einer Kurve $y=y(x)$ rollen kann. Bedeutet $m$ die Masse der Kugel, so ist die auf sie wirkende Schwerkraft

${\underset{\_}{G}}^T=(0;-mg;0)$

sie kann nach Einfiihrung der potentiellen Energie - auch Potential genannt -

$U=mgy+U_0;U_0=const$

auch in der Form

${\underset{\_}{G}}^T=-grad(U)=(\frac{\partial U}{\partial x};\frac{\partial U}{\partial y};\frac{\partial U}{\partial z})$

geschrieben werden. Nun konnen die oben dargestellten Gleichgewichtslagen dadurch charakterisiert werden, daß zum stabilen, labilen bzw. indifferenten Gleichgewicht ein Minimum ($U^{″}(x_1)>0$), Maximum ($U^{″}(x_1)<0$) bzw. "stationarer Wert" (U (x_3) = 0) der potentiellen Energie $U=mgy+U_0=mgy(x)+U_0=U(x)$ gehört.

Wir ersehen weiter aus obiger Abbildung, daß in der stabilen Gleichgewichtslage ($U=Minimum$) die Kugel bei einer kleinen Störung (d.h. Entfernung aus dieser Lage) um den im Vergleich zu den benachbarten tiefsten Punkt (kleine) Schwingungen ausführt. In Verallgemeinerung dieser Sachlage nennt man nach Klein, Felix (1849-1925) eine Gleichgewichtslage stabil, wenn für hinreichend klein gewählte Anfangsstörungen auch die Lageänderungen klein bleiben. Die allgemeine Gültigkeit des an einem Spezialfall gewonnenen Zusammenhanges zwischen potentieller Energie $U=U(x,y,z)$ und Gleichgewichtsart läßt sich wie folgt plausibel machen: Besitzen die (eingeprägten) Kräfte ein Potential, so gilt

${\underset{\_}{K}}_j=-gra{d}_j(U),U=\sum _{j=1}^n{U}_j$,

so daß also

$\delta A^e=\sum {\underset{\_}{K}}_j\cdot \delta {\underset{\_}{r}}_j=-\sum grad(U_j)\delta {\underset{\_}{r}}_j=-\sum \delta U_j=-\delta U$

ist. Dann gilt für dämpfungsfreie Systeme der Energiesatz

$E+U=const$, d.h. $\delta (E+U)=0$ (E ... kinetische Energie),

woraus mit dem Prinzip der virtuellen Vernickungen

$\delta E=-\delta U=\delta A^e=0$

folgt. Nun bedeutet dies, daß sowohl $E$ wie $U$ einen Extremwert besitzen: Entweder E = Maximum, U= Minimum oder umgekehrt. Passiert das System die durch $\delta A^e=0$ allgemein, durch E = Maximum, U= Minimum im besonderen charakterisierte Gleichgewichtslage, so hat E (als Maximum) die Tendenz zum Abnehmen, d. h. das System die Tendenz zur Ruckkehr in diese Lage, und das ist die Stabilität. Ist dagegen E = Minimum, U = Maximum, so hat E (als Minimum) die Tendenz zum Anwachsen, also das System die Neigung, sich mit wachsender Geschwindigkeit aus dieser Lage weiter zu entfernen: Instabilität.

In der Sprache der Differentialrechnung lassen sich die Gleichgewichtslagen, soweit eine Taylor-Entwicklung bis auf Glieder zweiter Ordnung zu diesem Zweck ausreivht", wie folgt festlegen:

$\delta U=-\delta A^e=0$,

 ${\delta }^{2}U=-{\delta }^2{A}^e(\begin{array}{cl}>0& \text{ ... stabile Lage,}\\ =0& \text{ ... indifferente Lage,}\\ <0& \text{ ... instabile Lage.}\end{array}$

Die Bedeutung des Differentials ${\delta }^{2}U$ (auch "zweite Variation" genannt) geht aus der Taylorschen Formel hervor:

$\begin{array}{ll}\delta U(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z+\mathrm{\Delta }z)& =U(x,y,z)+\delta U+\frac{1}{2!}{\delta }^{2}U+\dots \\ & =U+\frac{\partial U}{\partial x}\delta x+\frac{\partial U}{\partial y}\delta y+\frac{\partial U}{\partial z}\delta z\end{array}+\frac{1}{2!}(\frac{{\partial }^{2}U}{\partial x^2}\delta x^2+2\frac{{\partial }^{2}U}{\partial x\partial y}\delta x\delta y+\dots +\frac{{\partial }^{2}U}{\partial z^2}\delta z^2)+\dots$.

Weiter ist hieraus ersichtlich, daß es von dem Vorzeichen der zweiten Variation ${\delta }^{2}U$ abhängt, ob durch eine kleine - durch $\delta x,\delta y,\delta z$ gemessene - Lageänderung in zweiter Näherung Energie benötigt (Stabilität) oder frei wird (Instabilität).

Knoten eines allgemeinen Fachwerks.

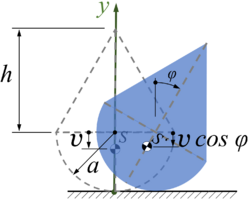
Beispiel: Homogene Halbkugel vom Radius a mit aufgesetztem Kreiskegel aus gleichem Material.

Wie groB ist h zu wählen, damit die skizzierte Gleichgewichtslage indifferent ist?

Da die Schwerpunkthöhen der Halbkugel bzw. des Kreiskegels $\frac{5}{8}a$ bzw. $\frac{1}{4}h$ sind, liegt der Gesamtschwerpunkt um

$\begin{array}{lll}v& =& a-y_{ges}\\ & =& a-\frac{\frac{5}{8}a\frac{2}{3}\pi a^3+\frac{1}{3}\pi a^{2}h(a+\frac{h}{4})}{\frac{2}{3}\pi a^3+\frac{1}{3}\pi a^{2}h}\\ & =& \frac{3a^2-h^2}{8a+4h}\end{array}$

unterhalb des Kugelmittelpunktes, so daß bei einer Drehung um den Winkel $\phi$ gegenüber der y-Achse der Gesamtschwerpunkt die Ordinate

$y_S=a-v\cos (\phi )$

hat. Die Gleichgewichtsbedingung (G = Gesamtgewicht)

$\delta A^e=-G\delta y_S=-G\frac{\partial y_S}{\partial \phi }\delta \phi =0$

liefert - da $\delta \phi$ beliebig ist - die Beziehung

$\frac{\partial y_S}{\partial \phi }=v\sin (\phi )=0$

die für die skizzierte Lage $\phi =0$ erfüllt ist. Die Bedingung des indifferenten Gleichgewichtes gemäß obiger Gleichung verlangt

${\delta }^2{A}^e=-G\frac{{\partial }^2{y}_S}{\partial {\phi }^2}\delta {\phi }^2=0$

also

$\frac{{\partial }^2{y}_S}{\partial {\phi }^2}=v\cos (\phi )=0$

woraus für $\phi =0$ schließlich $v=0$, also $\phi =0$ folgt.

Standsicherheitsmoment.

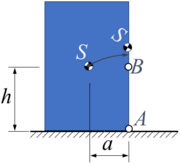
Eine Bemerkung: Als Maß für den Grad der Stabilität dient das sog. Standsicherheitemoment; das ist diejenige Arbeit, die aufgebracht werden muß, um einen starren Körper aus dem stabilen Gleichgewicht in diejenige Lage zu bringen, aus der er von selbst nicht mehr in die stabile Gleichgewichtslage zurückkehrt. Für das gezeichnete Parallelepiped vom Gewicht G wäre das Standsicherheitsmoment

$M_{St}=G\cdot \overline{S^{\prime }B}=G(\sqrt{a^2+h^2}-h)=Gh(\sqrt{1+{\left(\frac{a}{h}\right)}^2}-1)$.

Ist $a\ll h$ (z. B. bei einer Mauer), so liefert die binomische Reihe mit $G=2a2h\ell \gamma$ ($\gamma$ = spez. Gewicht, $\ell$ = Mauerlänge) die Näherungsformel

$M_{St}\approx 2a^3\ell \gamma$,

also einen von der Mauerhöhe $2h$ unabhängigen Wert!

Anwendungen des Prinzips der virtuellen Arbeiten auf die Elastizitiitstheorie
- Energiemethoden der Elastizitätslehre -

Zu ganz neuen Methoden und Erkenntnissen führt das Prinzip der virtuellen Arbeiten in der Elastizitätstheorie; wir beginnen mit einem einfachen Fall.

Das elastische Fachwerk

Knoten eines allgemeinen Fachwerks.

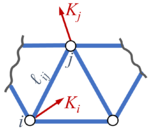
Bezeichnen wir die in den Knotenpunkten angreifenden Lasten mit

$\underset{\_}{K}=(X_j;Y_j;Z_j)$

die zugehörigen Verschiebungsvektoren mit

${\underset{\_}{v}}_j=(u_j;v_j;w_j)$,

so gehört zu diesen Kraften das Potential

$U_a=-\sum _j(X_j{u}_j+Y_j{v}_j+Z_j{w}_j)$

d.h., es besteht die Beziehung

${\underset{\_}{K}}_j=-gra{d}_j{U}_a=-(\frac{\partial U_a}{\partial u_j};\frac{\partial U_a}{\partial v_j};\frac{\partial U_a}{\partial w_j})$.

Hierzu tritt noch das zu den aus dem Hookeschen Gesetz folgenden Stabkräften

$S_{ij}=\frac{E_{ij}{A}_{ij}}{{\ell }_{ij}}\cdot \mathrm{\Delta }{\ell }_{ij}$

gemäß

$S_{ij}=\frac{\partial U_A}{\partial (\mathrm{\Delta }{\ell }_{ij})}$

gehörige Potential

$U_e=\frac{1}{2}\sum _{ij}\frac{E_{ij}{A}_{ij}}{{\ell }_{ij}}(\mathrm{\Delta }{\ell }_{ij}{)}^2$,

wobei $E_{ij}$ den Elastizitätsmodul, $A_{ij}$ den Stabquerschnitt, ${\ell }_{ij}$ die Stablänge und $\mathrm{\Delta }{\ell }_{ij}$ die Längenänderung des Stabes (i,j) bedeuten.

Das Fachwerk ist nach dem Prinzip der virtuellen Arbeiten in stabilem Gleichgewicht, wenn das Gesamtpotential

$U=U_a+U_e=-\sum _j(X_j{u}_j+Y_j{v}_j+Z_j{w}_j)+\sum _{ij}\frac{E_{ij}{A}_{ij}}{{\ell }_{ij}}(\mathrm{\Delta }{\ell }_{ij}{)}^2$,

ein Minimum ist, also $\delta U=0$ und ${\delta }^{2}U>0$ erfüllt sind, wobei die zwischen $\delta {\ell }_{ij}$ $u_j,v_j,w_j$ bestehenden Zusammenhange beachtet werden müssen.

Beispiel

Stabkraft im Fachwerks.

Stabkraft im Fachwerks.

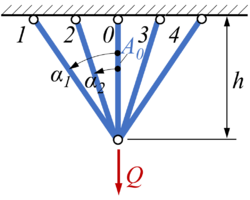
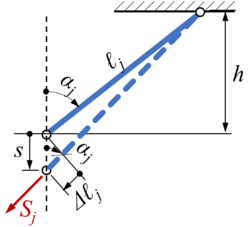
In dem aus 5 symmetrisch angeordneten Stäben bestehenden Fachwerk sollen die Stabquerschnitte bei gleichem Elastizititsmodul und gegebenen $A_0$ und $Q$ so gewählt werden, daß in allen Stäben die gleichen Zugkräfte auftreten.

Wie groß ist die lotrechte Verschiebung $s$ des Kraftangriffspunktes?

Das Gesamtpotential ist gemäß obiger Gleichung ist

$U=U_a+U_e=-Q\cdot s+\frac{E}{2}\sum _{j=0}^4\frac{A_j}{{\ell }_j}\cdot (\mathrm{\Delta }{\ell }_j{)}^2$.

Die notwendige Gleichgewichtsbedingung $\delta U=0$ liefert

$\delta U=-Q\cdot \delta s+E\sum _{j=0}^4\frac{A_j}{{\ell }_j}\cdot \mathrm{\Delta }{\ell }_j\delta (\mathrm{\Delta }{\ell }_j)$

Nun gilt, wenn wir von einer Anderung des Winkels ${\alpha }_j$ absehen

$\mathrm{\Delta }{\ell }_j=s\cdot \cos ({\alpha }_j)$

und somit

$\delta (\mathrm{\Delta }{\ell }_j)=\delta s\cdot \cos ({\alpha }_j)$

Damit geht aus $\delta U=0$

$(-Q+E\sum _{j=0}^4\frac{A_j}{{\ell }_j}\cdot s\cdot {\cos }^2({\alpha }_j))\cdot \delta s=0$

also mit ${\ell }_j=\frac{h}{\cos ({\alpha }_j)}$

$s=\frac{Qh}{E\sum _{j=0}^4{A}_j\cos ({\alpha }_j{)}^3}$

hervor. Für die Stabkräfte gilt nach dem Hookeschen Gesetz

$S_j=\frac{E{A}_j}{{\ell }_j}\mathrm{\Delta }{\ell }_j=\frac{E{A}_j}{h}s{\cos }^2(\alpha )=Q\frac{A_j{\cos }^2({\alpha }_j)}{\sum _{j=0}^4{A}_j{\cos }^3({\alpha }_j)}$.

Die Forderung $S_j=const$ ist erfüllt, wenn

$A_0\cdot 1=A_1\cdot {\cos }^2{\alpha }_1=A_2\cdot {\cos }^2{\alpha }_2$

ist, also $A_j=\frac{A_0}{{\cos }^2{\alpha }_j}$ gilt. Damit erhält man

$s=\frac{Qh}{E{A}_0\sum _{j=0}^4\cos {\alpha }_j}=\frac{Qh}{E{A}_0(1+2\cos {\alpha }_1+2\cos {\alpha }_2)}$

und

$S_j=\frac{Q}{\sum _{j=0}^4\cos {\alpha }_j}=\frac{Q}{(1+2\cos {\alpha }_1+2\cos {\alpha }_2)}$

Das Prinzip der virtuellen Verrückungen für linear elastische Systeme

Bei der allgemeinen Anwendung des Prinzips der virtuellen Arbeiten auf Probleme der Elastizitatstheorie spielt die Formanderungsarbeit W, wie in den Formeln von §1.2 dargelegt, eine zentrale Rolle. Hierfür beschreiben wir, wie in der "Einführung" dargelegt, den Deformationszustand eines (linear) elastischen Korpers durch die Dehnungen

Schnittlasten an einem kleinen Volumenelement.

${\epsilon }_{xx}=\frac{\partial u}{\partial x},{\epsilon }_{yy}=\frac{\partial v}{\partial y},{\epsilon }_{zz}=\frac{\partial w}{\partial z}$

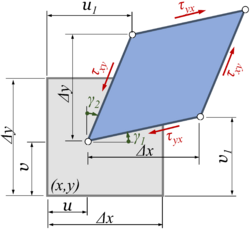
sowie durch Winkeländerungen (Gleitungen)

${\gamma }_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x},{\gamma }_{xz}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x},{\gamma }_{yz}=\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}$

der einzelnen Elemente.

🖌 Zur Nomenklatur:

Szabó verwendet in seinem Buch die Winkeländerungen ${\gamma }_{ij}$. Im Rest der Unterlagen wird ${\gamma }_{ij}=2\cdot {\epsilon }_{ij}$ verwendet. Außerdem ist ${\tau }_{ij}={\sigma }_{ij}$.

Gemäß den obigen Gleichungen gehören zu einer virtuellen Verschiebung

$\delta \underset{\_}{r}={(\delta u(x,y,z),\delta v(x,y,z);\delta w(x,y,z))}^T$

die virtuellen Dehnungen

$\delta {\epsilon }_{xx}=\frac{\partial \delta u}{\partial x},\delta {\epsilon }_{yy}=\frac{\partial \delta v}{\partial y},\delta {\epsilon }_{zz}=\frac{\partial \delta w}{\partial z}$

sowie die virtuellen Winkeländerungen (virtuellen Gleitungen)

$\delta {\gamma }_{xy}=\frac{\partial \delta u}{\partial y}+\frac{\partial \delta v}{\partial x},\delta {\gamma }_{xz}=\frac{\partial \delta u}{\partial z}+\frac{\partial \delta w}{\partial x},\delta {\gamma }_{yz}=\frac{\partial \delta v}{\partial z}+\frac{\partial \delta w}{\partial y}$.

Entsprechend diesen virtuellen Verzerrungen liefern die (inneren) Spannungen einen Anteil $\delta W$ zur gesamten virtuellen Arbeit des elastischen Systems.

Schnittlasten an einem kleinen Volumenelement.

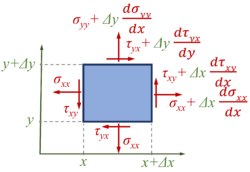
Zur Ermittlung des mit Rücksicht auf den "Energiesatz" zu den virtuellen Verrückungen wichtigen Anteils $\delta W$ betrachten wir ein Volumenelement $dV=dxdydz$, an dem außer den Normal- und Schubspannungen die je Volumeneinheit verstandene (eingeprägte) Kraft

$\underset{\_}{R}={(X,Y,Z)}^T$

angreifen möge. Bricht man die Taylorsche Entwicklung der Spannungen mit kleinen Größen erster Ordnung ab, so erhält man fur die virtuelle Arbeit sämtlicher äußerer, eingeprägter Kräfte am Element bei einer virtuellen Verschiebung $\delta \underset{\_}{r}=(\delta u,\delta v,\delta w)$ den Beitrag

$\begin{array}{lll}\delta (d{A}^e)& =& \delta (dA)=d(\delta A)\\ & =& \begin{array}{llll}& ({\sigma }_{xx}+\frac{\partial {\sigma }_{xx}}{\partial x}dx)& dydz& [\delta u+\frac{\partial }{\partial x}(\delta u)dx]-{\sigma }_{xx}dydz\delta u\\ +& ({\sigma }_{yy}+\frac{\partial {\sigma }_{yy}}{\partial y}dy)& dxdz& [\delta v+\frac{\partial }{\partial y}(\delta v)dy]-{\sigma }_{yy}dxdz\delta v\\ +& ({\sigma }_{zz}+\frac{\partial {\sigma }_{zz}}{\partial z}dz)& dxdy& [\delta w+\frac{\partial }{\partial z}(\delta w)dz]-{\sigma }_{zz}dxdy\delta w\\ +& ({\tau }_{xy}+\frac{\partial {\tau }_{xy}}{\partial x}dx)& dydz& [\delta v+\frac{\partial }{\partial x}(\delta v)dx]-{\tau }_{xy}dydz\delta v\\ +& ({\tau }_{yz}+\frac{\partial {\tau }_{yz}}{\partial y}dy)& dxdz& [\delta w+\frac{\partial }{\partial y}(\delta w)dy]-{\tau }_{yz}dxdz\delta w\\ +& ({\tau }_{zx}+\frac{\partial {\tau }_{zx}}{\partial z}dz)& dxdy& [\delta u+\frac{\partial }{\partial z}(\delta u)dz]-{\tau }_{zx}dxdy\delta u\\ +& ({\tau }_{xz}+\frac{\partial {\tau }_{xz}}{\partial x}dx)& dydz& [\delta w+\frac{\partial }{\partial x}(\delta w)dx]-{\tau }_{xz}dydz\delta w\\ +& ({\tau }_{yx}+\frac{\partial {\tau }_{yx}}{\partial y}dy)& dxdz& [\delta u+\frac{\partial }{\partial y}(\delta u)dy]-{\tau }_{yx}dxdz\delta u\\ +& ({\tau }_{zy}+\frac{\partial {\tau }_{zy}}{\partial z}dz)& dxdy& [\delta v+\frac{\partial }{\partial z}(\delta v)dz]-{\tau }_{zy}dxdy\delta v\\ \end{array}\\ & & +Xdxdydz\delta u+Ydxdydz\delta v+Zdxdydz\delta w\end{array}$

Nach Streichung von kleinen Größen fünfter Ordnung vereinfacht sich diese Gleichung zu

$\begin{array}{ll}d(\delta A)=[& {\sigma }_{xx}\frac{\partial }{\partial x}(\delta u)+\frac{\partial {\sigma }_{xx}}{\partial x}\delta u\\ & +{\sigma }_{yy}\frac{\partial }{\partial y}(\delta v)+\frac{\partial {\sigma }_{yy}}{\partial y}\delta v\\ & +{\sigma }_{zz}\frac{\partial }{\partial z}(\delta w)+\frac{\partial {\sigma }_{zz}}{\partial z}\delta w\\ & +{\tau }_{xy}\frac{\partial }{\partial x}(\delta v)+\frac{\partial {\tau }_{xy}}{\partial x}\delta v\\ & +{\tau }_{yx}\frac{\partial }{\partial y}(\delta u)+\frac{\partial {\tau }_{yx}}{\partial y}\delta u\\ & +{\tau }_{xz}\frac{\partial }{\partial x}(\delta w)+\frac{\partial {\tau }_{xz}}{\partial x}\delta w\\ & +{\tau }_{zx}\frac{\partial }{\partial z}(\delta u)+\frac{\partial {\tau }_{zx}}{\partial z}\delta u\\ & +{\tau }_{yz}\frac{\partial }{\partial y}(\delta w)+\frac{\partial {\tau }_{yz}}{\partial y}\delta w\\ & +{\tau }_{zy}\frac{\partial }{\partial z}(\delta v)+\frac{\partial {\tau }_{zy}}{\partial z}\delta v\\ & +X\delta u+Y\delta v+Z\delta w]& dxdydz\end{array}$

Wird nun z.B. das Element einer rein translatorischen verzerrungsfreien (virtuellen) Verrückung unterworfen ( $d(\delta A_i^e)=0$ - dies entspricht also einer Verschiebung eines starren Elements), so daß alle einer Winkeländerung des Elementes entsprechenden Größen $\frac{\partial (\delta v)}{\partial x},\frac{\partial (\delta w)}{\partial y},\frac{\partial (\delta u)}{\partial y},\frac{\partial (\delta w)}{\partial x},\frac{\partial (\delta v)}{\partial z},\frac{\partial (\delta u)}{\partial z}$ wie auch $\frac{\partial (\delta u)}{\partial x},\frac{\partial (\delta v)}{\partial y},\frac{\partial (\delta w)}{\partial z},$ verschwinden, so liefert die Gleichgewichtsbedingung mit $d(\delta A_i^e)=0$ am Element und $dV=dxdydz$

$\begin{array}{llll}d(\delta A_i^e)& =& & 0\\ & =& [& (\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}+X)\delta u\\ & =& +& (\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial z}+Y)\delta v\\ & =& +& (\frac{\partial {\sigma }_{zz}}{\partial z}+\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+Z)\delta v\end{array}$

Diese Beziehung kann für beliebige $\delta u,\delta v,\delta w$ nur dann erfüllt sein, wenn die Gleichungen

$\begin{array}{lll}\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}+X& =& 0\\ \frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial z}+Y& =& 0\\ \frac{\partial {\sigma }_{zz}}{\partial z}+\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+Z& =& 0\end{array}$

bestehen. Das sind die Gleichgewichtsbedingungen am Körperelement, wie wir sie schon in einem Spezialfall kennengelernt haben. Sie können freilich auch aus den Gleichgewichtsbedingungen der Kräfte in den drei Achsenrichtungen hergeleitet werden. Zu einer der Gleichgewichtsbedingung der Momente entsprechenden Aussage kommt man, indem man das Element einer reinen virtuellen Verdrehung unterwirft; das uns bekannte Resultat ist der Satz von den zugeordneten Schubspannungen:

${\tau }_{xy}={\tau }_{yx},{\tau }_{xz}={\tau }_{zx},{\tau }_{yz}={\tau }_{zy}$

Mit den obigen Gleichungen erhalten wir schließlich

$d(\delta A)=({\sigma }_{xx}\cdot \delta {\epsilon }_{xx}+{\sigma }_{yy}\cdot \delta {\epsilon }_{yy}+{\sigma }_{zz}\cdot \delta {\epsilon }_{zz}+{\tau }_{xy}\cdot \delta {\gamma }_{xy}+{\tau }_{yz}\cdot \delta {\gamma }_{yz}+{\tau }_{xz}\cdot \delta {\gamma }_{xz})dV$

und nach Integration tiber das gesamte Volumen

$\begin{array}{lll}\delta A& =& \underset{V}{\int }d(\delta A)dV\\ & =& \underset{V}{\int }({\sigma }_{xx}\cdot \delta {\epsilon }_{xx}+{\sigma }_{yy}\cdot \delta {\epsilon }_{yy}+{\sigma }_{zz}\cdot \delta {\epsilon }_{zz}+{\tau }_{xy}\cdot \delta {\gamma }_{xy}+{\tau }_{yz}\cdot \delta {\gamma }_{yz}+{\tau }_{xz}\cdot \delta {\gamma }_{xz})dV\\ & =& \underset{V}{\int }\delta W_{S}dV\\ & =& \delta W\\ \end{array}$

Durch diese Gleichung wird die mit den virtuellen Verrückungen verbundene Arbeit der eingeprägten Kräfte ausgedrückt durch die Änderung der von den Spannungen längs der entsprechenden Elementenverzerrungen geleisteten inneren Arbeit, die wir bereits oben als die Formanderungsarbeit W bezeichnet haben. Die gilt allgemein für elastische Systeme, und zwar für beliebige Elastizitatsgesetze (d.h. Zusammenhänge zwischen Spannungen und Verzerrungen), und sie läßt sich in der Form

$\delta (W-A)={\delta }_V(W-A)$

als ein sog. "Variationsprinzip" schreiben. Der Index V' bei dem Varia tionszeichen soll andeuten, daß bei diesem Prinzip die (stetig differenzierbaren) und mit den Randbedingungen verträglichen Verschiebungen (bzw. die in §10.3 näher erläuterten kompatiblen Verzerrungen) variiert werden; in diesem Sinne wollen wir vom Prinzip der virtuellen Verschiebungen sprechen. Das Prinzip beinhaltet auch, daß der in technisch wichtigen Fällen der Gleichgewichtslage eintretende Verzerrunqszustand derjenige ist, bei dem die Differenz $W-A$ ein Extremum (Minimum) wird. Auf eine entsprechende praktische Anwendung des Prinzips kommen wir in Ziffer 7 (Ritzsches Verfahren) zurück.