Sources/Lexikon/Lösungsschema der Statik
Zur Navigation springen
Zur Suche springen
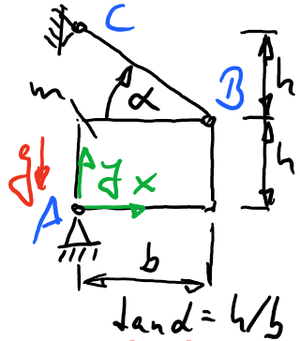
Lageplan 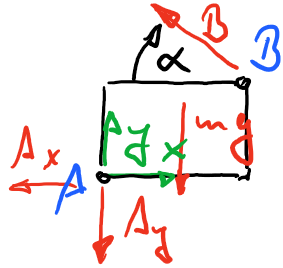
Freikörperbild 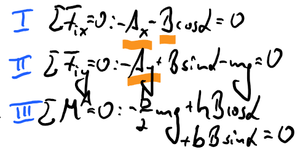
Gleichgewichtsbedingungen 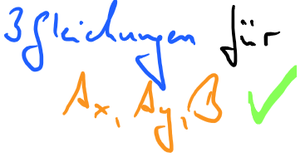
Gleichungen und Unbekannte abzählen
Lageplan

Freikörperbild

Gleichgewichtsbeidngungen
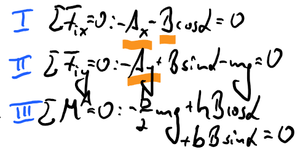
Gleichungen und Unbekannte abzählen
Lösen
- Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \begin{pmatrix}{{A}_{x}}=\displaystyle -\frac{\cos\left( \alpha\right) \cdot b\cdot g\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\cr {{A}_{y}}=\displaystyle -\frac{\sin\left( \alpha\right) \cdot b\cdot g\cdot m+2\cdot \cos\left( \alpha\right) \cdot g\cdot h\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\cr B=\displaystyle \frac{b\cdot g\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\end{pmatrix}} .
Maxima Code
Ein Skript zur Lösung in Maxima:
/* Maxima */
equs: [-A[x]-B*cos(alpha) = 0,
-A[y]+B*sin(alpha) -m*g = 0,
-b/2*m*g+h*B*cos(alpha) + b*B*sin(alpha) = 0];
q : [A[x],A[y],B];
sol: solve(equs,q)[1];
Ausdeuten der Lösung
![]() Achtung, das System in statisch unbestimmt, wenn die Systemdeterminante D verschwindet, also
Achtung, das System in statisch unbestimmt, wenn die Systemdeterminante D verschwindet, also
Das passiert für
Maxima Code
Ein Skript zur Ausdeutung der Lösung in Maxima:
D: determinant(submatrix(augcoefmatrix(equs,q),4));
