Gelöste Aufgaben/UEBJ

Aufgabenstellung

Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.

Für diese Aufgabe gibt es in UEBI eine analytische Lösung - hier schauen wir uns an, wie sich die Qualität der Näherungslösungen mit der Steigerung der Anzahl der Trial-Functions ändert.

Lageplan

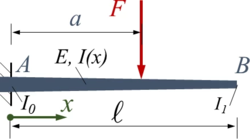
Gesucht ist die Biegeline und Schnittkraftverläufe mit dem Ansatz von Ritz und mehreren Trial-Funktionen.

Gegeben sind für den Balken:

• Länge ℓ, Breite b,
• E-Modul E, Dichte ρ und
• die Höhe h₀=b und h₁ jeweils in A und B; dazwischen ist die Höhe linear veränderlich.

Lösung mit Maxima

Beim Verfahren von Ritz arbeiten wir mit

• dem Prinzip vom Minimum der Potentiellen Energie und
• Ansatzfunktionen über die gesamte Länge des Balkens.

Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des einseitig fest eingespannten Balkens  mit konstanten I unter einer konstanten Streckenlast q₀. Hier ist die maximale Auslenkung

${\begin{array}{lcl}\displaystyle {\hat {w}}:={\frac {q_{ref}\,\ell ^{4}}{8EI_{ref}}}&{\text{ mit }}&q_{ref}=A_{ref}\,\rho \,g\\&&A_{ref}=h_{ref}\cdot b{\text{ und}}\\&&h_{ref}=\displaystyle {\frac {h_{0}+h_{1}}{2}}\end{array}}$.

Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken.

tmp

Header

Text

1+1

tmp

Declarations

Text

1+1

tmp

Rayleigh-Ritz Approach

Text

1+1

tmp

Post-Processing

Text

1+1

---

Links

• ...

Literature

• ...

Parameterstudie: Biegelinie w(x)

Parameterstudie Biegemomentenverlauf M(x)

Parameterstudie Querkraftverlauf Q(x)

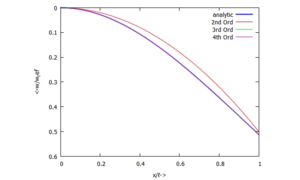
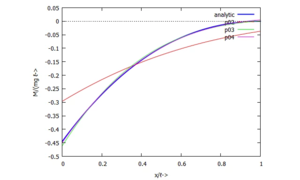
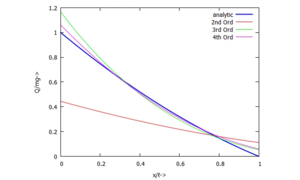
h