Gelöste Aufgaben/UEBI

Aufgabenstellung

Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.

In UEBF haben wir eine Näherungslösung für dieses Problem berechnet.

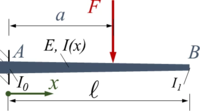
Gesucht ist die analytische Lösung des Problems.

Gegeben sind für den Balken:

Länge ℓ, Breite b,
E-Modul E, Dichte ρ und
die Höhe h₀=b und h₁ jeweils in A und B; dazwischen ist die Höhe linear veränderlich.

Lösung mit Maxima

Um zur analytischen Lösung zukommen, müssen wir berücksichtigen, dass

$E I (x) \cdot \frac{d^{2}}{d x^{2}} w (x) = - M (x)$ .

Wir müssen also hier die Abhängigkeit der Querschnittseigenschaften von "x" in der Differentialbeziehung berücksichtigen. Das macht die Sache deutlich komplizierter als vorher.

tmp

Wir haben die Differential-Beziehungen

$\begin{array}{rcl} Q^{'} & = & - q \\ M^{'} & = & + Q \\ E I \cdot ϕ^{'} & = & - M \\ w^{'} & = & + ϕ \end{array}$

für die Querkraft Q, das Moment M, die Verkippung der Querschnitte ϕ und die Auslenkung w. Dabei ist die ortsabhängige Streckenlast

$q (x) = A (x) ρ g mit A (x) = b \cdot h (x) .$

Die Höhe des Balkens ist linear veränderlich, nämlich

$h (x) = h_{0} (1 - ξ) + h_{1} ξ mit ξ = \frac{x}{ℓ}$ .

Header

Text

tmp

Diese Abkürzungen führen wir ein:

$m = ρ \frac{h_{0} + h_{1}}{2} b ℓ g$ ,

$h_{1} = α h_{0}$ .

Für die Ergebnisse setzten wir dann exemplarisch

$α = \frac{1}{2}$

an - sonst werden die Ausdrücke zu umfangreich.

Declarations

Text

tmp

Beim Aufintegrieren der Differentialgleichungen stören die vielen dimensionsbehafteten Parameter. Viel einfacher werden die Gleichungen, wenn wir sie in dimensionsloser Form - mit dimensionsloser Auslenkung, Kippwinkel, Biegemoment und Querkraft anschreiben, also

$\begin{array}{lcc} w & = W_{r e f} & \cdot & \tilde{w} \\ ϕ & = Φ_{r e f} & \cdot & \tilde{ϕ} \\ M & = M_{r e f} & \cdot & \tilde{M} \\ Q & = Q_{r e f} & \cdot & \tilde{Q} \end{array}$ .

Wir wählen dazu als Referenzlösung den Kragbalken mit konstantem Querschnitt unter konstanter Streckenlast, mit der maximalen Auslenkung

$W_{r e f} = \frac{q_{r e f} ℓ^{4}}{8 E I_{r e f}}$ .

Als Referenz-Werte für die Streckenlast wählen wir hier die Werte unseres Balkens in x=ℓ/2, demnach

$\begin{array}{ll} q_{r e f} & = A_{r e f} ρ g mit A_{r e f} = b \cdot h (\frac{ℓ}{2}) \\ I_{r e f} & = \frac{b \cdot h (\frac{ℓ}{2})^{3}}{12} \end{array}$ .

Die Differentialgleichungen werden dadurch und mit der dimensionslosen Ortskoordinate

$ξ = \frac{x}{ℓ}$

viel einfacher, nämlich

$\begin{array}{rcl} \frac{\partial}{\partial ξ} \tilde{Q} & = & - \frac{4 - 2 ξ}{3} \\ \frac{\partial}{\partial ξ} \tilde{M} & = & + \tilde{Q} \\ \frac{\partial}{\partial ξ} \tilde{ϕ} & = & - \frac{8}{\frac{I (ξ)}{I_{r e f}}} \cdot \tilde{M} mit \frac{I (ξ)}{I_{r e f}} = \frac{(α + 1)^{3}}{8 ((α - 1) ξ + 1)^{3}} \\ \frac{\partial}{\partial ξ} \tilde{w} & = & + \tilde{ϕ} \end{array}$ .

Damit es übersichtlicher wird, lassen wir die Tilden über den gesuchten dimensionslosen Funktionen gleich wieder weg.

Dimensionless Form of Differential Equations

Text

tmp

Die Differentialbeziehungen lösen wir nun sukzessive zu

$Q (ξ) = \frac{ξ^{2} - 4 ξ + 3 C_{3}}{3}$ ,

$M (ξ) = \frac{ξ^{3} - 6 ξ^{2} + 9 C_{3} ξ + 9 C_{2}}{9}$ .

Bis hier ist alles wie gehabt - aber jetzt steht das ortsveränderliche Flächenmoment I(ξ) im Nenner. Maxima liefert

$ϕ (ξ)) = \frac{6 ξ^{3} + (2 C_{1} - 24) ξ^{2} + (- 54 C_{3} - 8 C_{1} + 96) ξ + 54 C_{3} - 27 C_{2} + 8 C_{1} - 96}{2 ξ^{2} - 8 ξ + 8}$

und im nächsten Schritt schließlich

$w (ξ) = \frac{3 ξ^{3} + (2 C_{1} - 6) ξ^{2} + ((72 - 54 C_{3}) \ln (- \frac{ξ - 2}{2}) - 4 C_{1} + 2 C_{0}) ξ + (108 C_{3} - 144) \ln (- \frac{ξ - 2}{2}) + 54 C_{3} + 27 C_{2} - 4 C_{0} - 48}{2 ξ - 4}$ .

Darin enthalten sind die unbekannten - also gesuchten - Integrationskonstanten

$C_{0}, C_{1}, C_{2}, C_{3}$ .

Integration Of Differential Equation

Text

tmp

Diese Unbekannten bestimmen wir aus den Randbedingungen, nämlich

$\begin{array}{rcl} w (0) & = & 0 \\ ϕ (0) & = & 0 \\ M (1) & = & 0 \\ Q (1) & = & 0 \end{array}$

und damit

$\begin{array}{rcl} 0 & = & C_{3} - 1 \\ 0 & = & 9 C_{3} + 9 C_{2} - 5 \\ 0 & = & 54 C_{3} - 27 C_{2} + 8 C_{1} - 96 \\ 0 & = & - 54 C_{3} - 27 C_{2} + 4 C_{0} + 48 \end{array}$ .

Boundary Conditions

Text

tmp

Zum Lösen bringen wir die Gleichungen in die Form

$(\begin{matrix} 0 & 0 & 0 & - 3 \\ 0 & 0 & - 9 & - 9 \\ 0 & - 8 & 27 & - 54 \\ - 4 & 0 & 27 & 54 \end{matrix}) \cdot (\begin{matrix} C_{0} \\ C_{1} \\ C_{2} \\ C_{3} \end{matrix}) = (\begin{matrix} - 3 \\ - 5 \\ - 96 \\ 48 \end{matrix})$ ,

die wir lösen zu

$\begin{array}{lcc} C_{0} & = & - \frac{3}{2}, \\ C_{1} & = & + \frac{15}{4}, \\ C_{2} & = & - \frac{4}{9}, \\ C_{3} & = & + 1 \end{array}$ .

Solving

Text

tmp

Die Ergebnisse schauen wir uns in dimensionsloser Form an, wobei wir die Standard-Lösungen für den Balken unter konstanter Streckenlast ansetzen.

Für

\begin{array}{lcl} W_{r e f} & = & \frac{q_{r e f} \cdot ℓ^{4}}{8 E I_{r e f}}, \\ Φ_{r e f} & = & \frac{W_{r e f}}{ℓ}, \\ M_{r e f} & = & m \cdot g \cdot ℓ, \\ Q_{r e f} & = & m \cdot g, \\ q_{r e f} & = & m \cdot g / ℓ, \\ E I_{r e f} & = & E \cdot \frac{b \cdot ((H_{0} + H_{1}) / 2)^{3}}{12} \end{array}

finden wir

... für w(ξ):
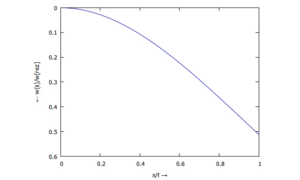
Auslenkung w(x)
... für ϕ(ξ):
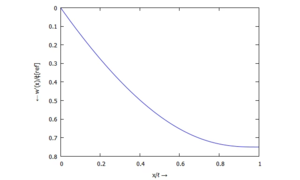
Querschnitts-Kippung w'(x)
... für M(ξ):
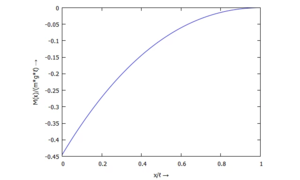
Momentenverlauf M(x)
... für Q(ξ):
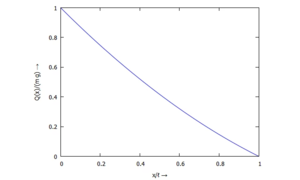
Querkraftverlauf Q(x)

Post-Processing

Text

Plot Data

Datenpunkte für die Auftragung von w(x)
Hier gibt's die Datenpunkte für w(x) zum Herunterladen.

data

toggle: data listing →

table for ← w(x)/w[rez] 
0.0 ; 0.0 
0.01 ; 7.481203031248985*10^-5 
0.02 ; 2.984924700020887*10^-4 
0.03 ; 6.698993034749879*10^-4 
0.04 ; 0.001187879040283986 
0.05 ; 0.00185126660292937 
0.06 ; 0.002658885214942354 
0.07 ; 0.003609546289359847 
0.08 ; 0.004702049317703514 
0.09 ; 0.005935181759589655 
0.1 ; 0.007307718933097404 
0.11 ; 0.008818423906038287 
0.12 ; 0.01046604738827592 
0.13 ; 0.01224932762526032 
0.14 ; 0.01416699029293324 
0.15 ; 0.01621774839421548 
0.16 ; 0.01840030215723649 
0.17 ; 0.02071333893554073 
0.18 ; 0.02315553311047674 
0.19 ; 0.02572554599601331 
0.2 ; 0.02842202574623001 
0.21 ; 0.03124360726574977 
0.22 ; 0.03418891212340282 
0.23 ; 0.0372565484694203 
0.24 ; 0.04044511095649053 
0.25 ; 0.04375318066501066 
0.26 ; 0.04717932503291399 
0.27 ; 0.05072209779045508 
0.28 ; 0.0543800389003753 
0.29 ; 0.05815167450388911 
0.3 ; 0.06203551687296655 
0.31 ; 0.06603006436941357 
0.32 ; 0.07013380141128575 
0.33 ; 0.07434519844720817 
0.34 ; 0.07866271193920962 
0.35 ; 0.08308478435471277 
0.36 ; 0.08760984416838222 
0.37 ; 0.09223630587454254 
0.38 ; 0.09696257001097904 
0.39 ; 0.1017870231949183 
0.4 ; 0.1067080381721125 
0.41 ; 0.1117239738799426 
0.42 ; 0.1168331755255615 
0.43 ; 0.1220339746801493 
0.44 ; 0.1273246893904267 
0.45 ; 0.1327036243086318 
0.46 ; 0.1381690708422802 
0.47 ; 0.1437193073250795 
0.48 ; 0.1493525992104727 
0.49 ; 0.1550671992894059 
0.5 ; 0.160861347933972 
0.51 ; 0.1667332733687484 
0.52 ; 0.1726811919717323 
0.53 ; 0.1787033086069086 
0.54 ; 0.1847978169906433 
0.55 ; 0.1909629000942185 
0.56 ; 0.1971967305850093 
0.57 ; 0.2034974713089322 
0.58 ; 0.2098632758170441 
0.59 ; 0.2162922889392689 
0.6 ; 0.2227826474085497 
0.61 ; 0.229332480538859 
0.62 ; 0.2359399109607717 
0.63 ; 0.2426030554186048 
0.64 ; 0.2493200256333157 
0.65 ; 0.2560889292357581 
0.66 ; 0.2629078707751271 
0.67 ; 0.2697749528078152 
0.68 ; 0.2766882770722823 
0.69 ; 0.2836459457558966 
0.7 ; 0.2906460628602184 
0.71 ; 0.2976867356715562 
0.72 ; 0.3047660763442248 
0.73 ; 0.3118822036044391 
0.74 ; 0.3190332445833526 
0.75 ; 0.3262173367883804 
0.76 ; 0.3334326302226785 
0.77 ; 0.340677289663329 
0.78 ; 0.3479494971096025 
0.79 ; 0.3552474544135462 
0.8 ; 0.3625693861060849 
0.81 ; 0.3699135424327804 
0.82 ; 0.3772782026145832 
0.83 ; 0.3846616783500371 
0.84 ; 0.392062317576676 
0.85 ; 0.3994785085108331 
0.86 ; 0.4069086839865492 
0.87 ; 0.4143513261159026 
0.88 ; 0.4218049712949479 
0.89 ; 0.4292682155813812 
0.9 ; 0.4367397204721419 
0.91 ; 0.4442182191116147 
0.92 ; 0.4517025229634247 
0.93 ; 0.4591915289818366 
0.94 ; 0.4666842273215563 
0.95 ; 0.4741797096282359 
0.96 ; 0.4816771779554077 
0.97 ; 0.4891759543576916 
0.98 ; 0.4966754912143446 
0.99 ; 0.5041753823419752 
1.0 ; 0.5116753749604923

Links

...

Literature

...

Gelöste Aufgaben/UEBI

Inhaltsverzeichnis

Aufgabenstellung

Lösung mit Maxima