Gelöste Aufgaben/TC13

Aufgabenstellung

Das System ist eine Variante von Aufgabe TC12. Hier ist eine Näherungslösung mit der Methode der Finiten Elemente gefragt. Das Sytem besteht aus zwei Sektionen mit den Längen ℓ₁ bzw. ℓ₂ sowie den Flächenmomenten I₁ bzw. I₂. Sektion AB ist durch eine konstante Streckenlast q₀ belastet, in B wirkt das Moment M_B0. Der Stab ist in A durch ein gelenkiges Festlager gelagert. In C ist das Stabende fest mit dem Umfang einer Rolle vom Radius r verbunden, die in D frei drehbar gelagert ist. In B sind die beiden Sektionen fest miteinander verbunden. Die Feder in B ist eine Translationsfeder mit der Steifigkeit  k_B.

Lageplan

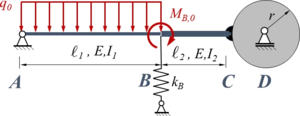
Gesucht ist die FEM-Lösung mit zwei Elementen für den Euler-Bernoulli-Balken.

Die Systemparameter sind die gleichen wie in TC12, das dort gesuchte Flächenmoment I₁ übernehmen wir zu

$I_{1}=54\,000{\text{ mm}}^{4}$.

Lösung mit Maxima

Header

Wir suchen eine Lösung mit den Standard-Trial-Functions (Hermitesche-Polynome) für einen Euler-Bernoulli-Balken. Aufpassen müssen wir am Rand "C". Hier sind Verschiebung und Verdrehung durch die Rolle gekoppelt. Die Element-Steifigkeitsmatrix müssen wir passend umschreiben.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2018-04-15                            */
/* ref: TM-C, Labor 4                                  */
/* description: finds the FE solution for              */
/*              lab problem #4                         */
/*******************************************************/

/* declare variational variables - see 6.3 Identifiers */
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δW", alphabetic);
declare("δΦ", alphabetic);
declare("δw", alphabetic);

Declarations

Wir übernehmen die Systemparameter aus TC12 zu

${\begin{array}{l}\displaystyle {\ell _{1}}=1000\cdot {\mathit {mm}},\\\displaystyle {\ell _{2}}={\frac {\ell _{1}}{2}},\\\displaystyle r={\frac {\ell _{1}}{4}},\\\displaystyle E={\frac {210000.0\cdot N}{{\mathit {mm}}^{2}}},\\\displaystyle {{I}_{1}}=54000\cdot {{\mathit {mm}}^{4}},\\\displaystyle {{I}_{2}}=2\cdot {{I}_{1}},\\\displaystyle {{k}_{B}}={\frac {3\cdot {{I}_{1}}\cdot E}{\ell _{1}^{3}}},\\\displaystyle {{q}_{0}}={\frac {10\cdot N}{\mathit {mm}}},\\\displaystyle {{M}_{B}}={{q}_{0}}\cdot {\ell _{1}^{2}}\end{array}}$,

und wählen als Referenzgröße w_ref für die Auslenkung des Balkens die maximale Verschiebung eines Kragbalkens unter konstanter Streckenlast:

$\displaystyle w_{ref}={\frac {q_{o}\;\ell _{1}^{4}}{8\;E\,I_{1}}}$.

/*** declarations ***/
assume(l[i]>0);

/* system parameter */
units  : [mm = m/1000, cm = m/100];
params : [l[1]=1000*mm, l[2] = l[1]/2, r=l[1]/4,
          E    = 2.1*10^5*N/mm^2,
          I[1] = 54000*mm^4, I[2]=2*I[1],
          k[B] = 3*E*I[1]/l[1]^3,
          q[0]=10*N/mm, M[B]=q[0]*l[1]^2];

params : subst(units,makelist(lhs(params[i])=subst(params,rhs(params[i])),i,1,length(params)));

/* kinematics of boundary condition at "C" */
kinematics : [W[2]=-r*Φ[2], δW[2] = -r*δΦ[2]];

/* max. displacement of cantilevered beam under load q[0] */
dimless : [w[ref] = q[0]*l[1]^4/(8*E*I[1])];
print(subst(params,dimless))$

Formfunctions

Die Trial-Functions je Element "i" zur Komposition der Form-Funktion kopieren wir aus Finite Elemente Methode zu

${\begin{array}{l}\phi _{1}=2\cdot {{\xi }^{3}}-3\cdot {{\xi }^{2}}+1,\\\phi _{2}={{\ell }_{i}}\cdot \left({{\xi }^{3}}-2\cdot {{\xi }^{2}}+\xi \right),\\\phi _{3}=3\cdot {{\xi }^{2}}-2\cdot {{\xi }^{3}},\\\phi _{4}={{\ell }_{i}}\cdot \left({{\xi }^{3}}-{{\xi }^{2}}\right)\end{array}}$,

die Koordinaten der Verschiebung sind

$Q_{i}=\left({\begin{array}{l}W_{i-1}\\\Phi _{i-1}\\W_{i}\\\Phi _{i}\end{array}}\right)$.

Damit ist

${\begin{array}{lcll}w_{i}(x_{i})=&&W_{i-1}&\cdot \left(2\cdot {{\xi }^{3}}-3\cdot {{\xi }^{2}}+1\right)\\&+&\Phi _{i-1}&\cdot {{\ell }_{i}}\cdot \left({{\xi }^{3}}-2\cdot {{\xi }^{2}}+\xi \right)\\&+&W_{i}&\cdot \left(3\cdot {{\xi }^{2}}-2\cdot {{\xi }^{3}}\right)\\&+&\Phi _{i}&\cdot {{\ell }_{i}}\cdot \left({{\xi }^{3}}-{{\xi }^{2}}\right)\end{array}}$.

/**** define form functions ***/
/* coordinates */
coords : [[ W[i-1], Φ[i-1], W[i], Φ[i]],
          [δW[i-1],δΦ[i-1],δW[i],δΦ[i]]];

/* tial-functions */
phi : [ 2*xi^3-3*xi^2+1,
       (xi^3-2*xi^2+xi)*l[i],
        3*xi^2-2*xi^3,
       (xi^3-xi^2)*l[i]];

/* form-function */
form : w(xi) = sum(coords[1][j]*phi[j],j,1,4);

Equilibrium Conditions

Die Gleichgewichtsbedingungen kommen aus dem Prinzip der virtuellen Verrückungen zu

${\begin{array}{ll}\delta W&{\stackrel {!}{=}}0\\&=\delta W_{a}-\delta \Pi \end{array}}$.

Wir sortieren die Elemente der virtuellen Arbeit nach den virtuellen Koordinaten und den Koordinaten des System und konstruieren daraus das gewöhnliche Gleichungssystem

${\underline {\underline {K}}}\cdot {\underline {Q}}={\underline {P}}$.

Die Anteile an der gesamten virtuellen Arbeit kommen aus der virtuellen Formänderungsenergie δΠ und der virtuellen Arbeit der äußeren Lasten δW^a.

Dabei ist für unsere zwei Elemente δΠ = δΠ₁ + δΠ₂' mit

$\delta \Pi _{i}=\delta {\underline {Q}}_{i}^{T}\cdot {\underline {\underline {k}}}_{0}\cdot {\underline {Q_{i}}}$

und der Element-Steifigkeitsmatrix

${\underline {\underline {k}}}_{0}=\displaystyle {\frac {\mathit {EI}}{{\ell }_{i}^{3}}}\cdot {\begin{pmatrix}12&6\cdot {{\ell }_{i}}&-12&6\cdot {{\ell }_{i}}\\6\cdot {{\ell }_{i}}&4\cdot {{\ell }_{i}^{2}}&-6\cdot {{\ell }_{i}}&2\cdot {{\ell }_{i}^{2}}\\-12&-6\cdot {{\ell }_{i}}&12&-6\cdot {{\ell }_{i}}\\6\cdot {{\ell }_{i}}&2\cdot {{\ell }_{i}^{2}}&-6\cdot {{\ell }_{i}}&4\cdot {{\ell }_{i}^{2}}\end{pmatrix}}$.

Für Element 1 können wir diese Matrix direkt übernehmen, das heißt k₁ = k₀ für i=1.

Element 2 birgt eine Tücke: Hier sind Verschiebung W₂ und Verdrehung Φ₂ gekoppelt über die Kinematik der Rolle:

$W_{2}=-r\cdot \Phi _{2}$

Damit ist auch die Variation in diesen Koordinaten gekoppelt, also

$\delta W_{2}=-r\cdot \delta \Phi _{2}$.

Mit dieser Beziehung eliminieren wir demnach W₂ aus der Formulierung der Gleichgewichtsbedingungen. Das Einsetzen der kinematischen Beziehungen in δΠ liefert nun als Element-Steifigkeitsmatrix

${\underline {\underline {k}}}_{2}=\displaystyle {\frac {E\,I_{2}}{l_{2}^{3}}}\cdot {\begin{pmatrix}12&6\cdot {{\ell }_{2}}&0&12\cdot r+6\cdot {{\ell }_{2}}\\6\cdot {{\ell }_{2}}&4\cdot {{\ell }_{2}^{2}}&0&6\cdot {{\ell }_{2}}\cdot r+2\cdot {{\ell }_{2}^{2}}\\0&0&0&0\\12\cdot r+6\cdot {{\ell }_{2}}&6\cdot {{\ell }_{2}}\cdot r+2\cdot {{\ell }_{2}^{2}}&0&12\cdot {{r}^{2}}+12\cdot {{\ell }_{2}}\cdot r+4\cdot {{\ell }_{2}^{2}}\end{pmatrix}}$,

bei der die Elemente der dritten Zeile (zu δW_i) und der dritten Spalte (zu W_i) verschwinden.

Struktur der Steifigkeitsmatrix.

Wir setzen die Gesamt-Steifigkeitsmatrix K aus den beiden Element-Steifigkeitsmatrizen so zusammen:

Und das ist die anteilige Gesamt-Steifigkeitsmatrix der beiden Balken-Abschnitte:

${\underline {\underline {K}}}\,=\,{\begin{pmatrix}{\frac {12\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{3}}}&{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&-{\frac {12\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{3}}}&{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&0&0\\{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {4\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {2\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&0&0\\-{\frac {12\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{3}}}&-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {12\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{3}}}+{\frac {12\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{3}}}&{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&0&{\frac {12\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{3}}}+{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}\\{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {2\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {4\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}+{\frac {4\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&0&{\frac {6\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{2}}}+{\frac {2\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}\\0&0&0&0&0&0\\0&0&{\frac {12\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{3}}}+{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}&{\frac {6\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{2}}}+{\frac {2\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}&0&{\frac {12\cdot {{I}_{2}}\cdot {{r}^{2}}\cdot E}{{\ell }_{2}^{3}}}+{\frac {12\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{2}}}+{\frac {4\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}\end{pmatrix}}$

Auch die Feder ist ein elastisches Element und trägt damit eine virtuelle Formänderungsenergie, zu δΠ hinzu, nämlich

$\delta \Pi _{3}=k_{B}\,W_{1}\cdot \delta W_{1}$

Diesen Beitrag müssen wir in Zeile 3, Spalte 3 hinzuaddieren, also mit der Anweisung

$K_{3,3}=K_{3,3}+k_{B}$.

Auf der rechten Seite des Gleichungssystem bleiben die Beiträge der virtuellen Arbeiten äußerer Lasten stehen. Dies sind

$\delta W^{a}=\int _{\ell _{1}}q_{0}\cdot \delta w(x)\,dx+M_{B}\cdot \delta \Phi _{1}$,

wir erhalten

${\underline {P}}\,=\,{\begin{pmatrix}\displaystyle {\frac {{{q}_{0}}\cdot {{\ell }_{1}}}{2}}\\\displaystyle {\frac {{{q}_{0}}\cdot {{\ell }_{1}^{2}}}{12}}\\\displaystyle {\frac {{{q}_{0}}\cdot {{\ell }_{1}}}{2}}\\\displaystyle {{M}_{B}}-{\frac {{{q}_{0}}\cdot {{\ell }_{1}^{2}}}{12}}\\\displaystyle 0\\\displaystyle 0\end{pmatrix}}$.

Jetzt fehlen nur noch die Randbedingungen. Wir setzen

$W_{0}=0$,

die kinematische Beziehung

$W_{2}=-r\cdot \Phi _{2}$

haben wir schon eingearbeit - bleibt also nur noch, die entsprechenden Spalten und Zeilen in den Matrizen K, Q und P zu eliminieren. Es bleibt das Gleichungssystem

${\begin{pmatrix}{\frac {4\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {2\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&0\\-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {12\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{3}}}+{\frac {12\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{3}}}+{{k}_{B}}&{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {12\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{3}}}+{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}\\{\frac {2\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}-{\frac {6\cdot {{I}_{1}}\cdot E}{{\ell }_{1}^{2}}}&{\frac {4\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}+{\frac {4\cdot {{I}_{1}}\cdot E}{{\ell }_{1}}}&{\frac {6\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{2}}}+{\frac {2\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}\\0&{\frac {12\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{3}}}+{\frac {6\cdot {{I}_{2}}\cdot E}{{\ell }_{2}^{2}}}&{\frac {6\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{2}}}+{\frac {2\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}&{\frac {12\cdot {{I}_{2}}\cdot {{r}^{2}}\cdot E}{{\ell }_{2}^{3}}}+{\frac {12\cdot {{I}_{2}}\cdot r\cdot E}{{\ell }_{2}^{2}}}+{\frac {4\cdot {{I}_{2}}\cdot E}{{\ell }_{2}}}\end{pmatrix}}\,\cdot \,{\begin{pmatrix}{{\Phi }_{0}}\\{{W}_{1}}\\{{\Phi }_{1}}\\{{\Phi }_{2}}\end{pmatrix}}\,=\,{\begin{pmatrix}{\frac {{{q}_{0}}\cdot {{\ell }_{1}^{2}}}{12}}\\{\frac {{{q}_{0}}\cdot {{\ell }_{1}}}{2}}\\{{M}_{B}}-{\frac {{{q}_{0}}\cdot {{\ell }_{1}^{2}}}{12}}\\0\end{pmatrix}}$.

1+1

Solving

Auflösen nach Q liefert

${\begin{array}{ll}{\Phi _{0}}&=-0.0157,\\W_{1}&=-4.86\cdot {{10}^{-18}}\;{\text{m}},\\{\Phi _{1}}&=+0.0682,\\{\Phi _{2}}&=-0.0262\end{array}}$,

zusammen mit den {\color{green}Randbedingungen} also

${\begin{array}{ll}{\color {green}{W_{0}}}&={\color {green}{0}},\\{\Phi _{0}}&=-0.0157,\\W_{1}&=-4.86\cdot {{10}^{-18}}\;{\text{m}},\\{\Phi _{1}}&=+0.0682,\\{\color {green}{W_{2}}}&={\color {green}{+0.00656{\text{ m}}}},\\{\Phi _{2}}&=-0.0262\end{array}}$.

/**** solve K Q = P ***/

sol[1] : linsolve_by_lu(subst(params,K),subst(params,P))[1]$
sol[1] : makelist(Q[i][1] = sol[1][i][1],i,1,4);
sol[1] : append(subst(params,[W[0]=0, W[2]=-r*subst(sol[1], Φ[2])]), sol[1]);

Post-Processing

Biegelinie w(x)

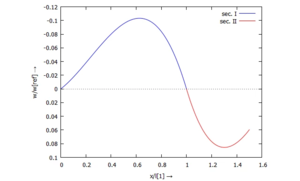
Die Auslenkung w(x) der Querschnitte tragen wir jetzt auf. Für die dimensionslose Darstellung wählen wir aus der analytischen Lösung für den Kragbalken unter konstanter Streckenlast

${\begin{array}{ll}{{w}_{\mathit {ref}}}&\displaystyle ={\frac {{{q}_{0}}\cdot {{\ell }_{1}^{4}}}{8\cdot E\,{{I}_{1}}}}\\&=0.11{\text{ m}}\end{array}}$

und tragen w(x)/w_ref auf:

Die maximale Auslenkung des Systems ist dann

${\begin{array}{ll}w_{max}&\approx 0.1\cdot 0.11{\text{ m}}\\&\approx 11{\text{ mm}}\end{array}}$,

und das entspricht der Vorgabe aus Aufgabe TC12.

/**** post-process  ***/
f1 : subst([xi=t],subst(params,subst(dimless,expand(subst(sol[1],subst([i=1],subst(form,w(xi)/w[ref])))))));
f2 : subst([xi=t],subst(params,subst(dimless,expand(subst(sol[1],subst([i=2],subst(form,w(xi)/w[ref])))))));
scale : subst(params,(l[2]/l[1]));

plot2d([[parametric,   t,       f1, [t, 0, 1]],
        [parametric, 1+t*scale, f2, [t, 0, 1]]],
       [gnuplot_preamble, "set yrange [] reverse"],
       [legend, "sec. I", "sec. II"],
       [xlabel, "x/l[1] →"], [ylabel, "w/w[ref] →"])$

---

Links

• ...

Literature

• ...