Gelöste Aufgaben/SKEB

Aufgabenstellung

Die Bewegung des Balkens wird durch das Zusammenspiel von elastischen Verformungen und Trägheitskräften bestimmt. Man nennt das "Schwingungen von Kontinua" - diese untersuchen wir hier. Der zentrale Aufgabe besteht in der Berechnung der homogenen Lösung - und der Anpassung der Lösungsanteile an die Anfangsbedingungen.

Lageplan

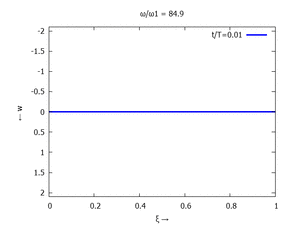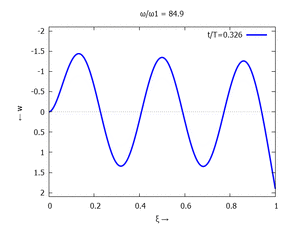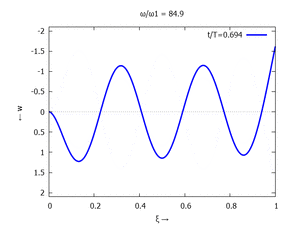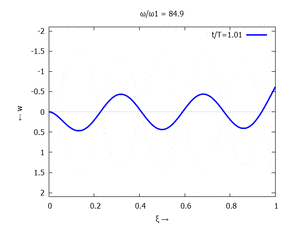
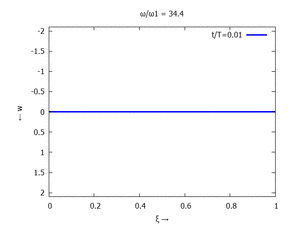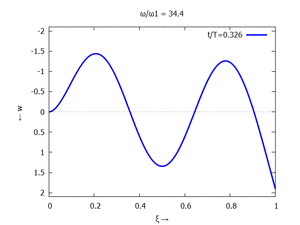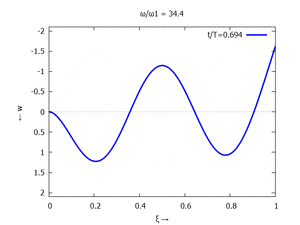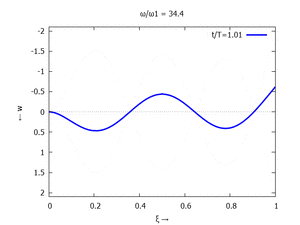
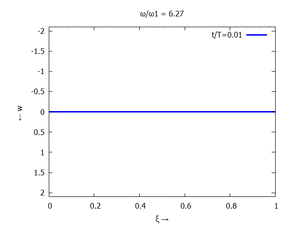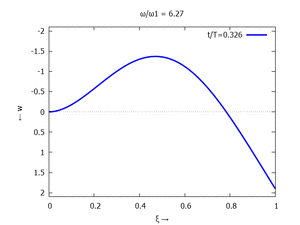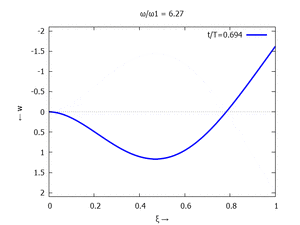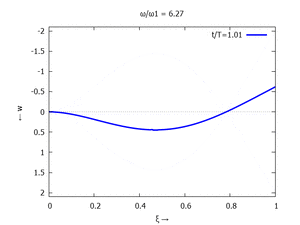
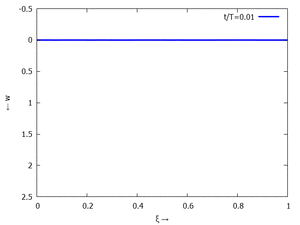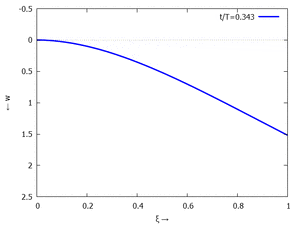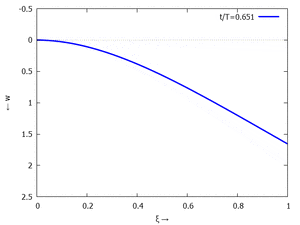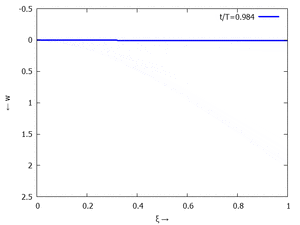
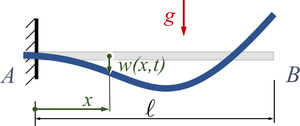
Gesucht ist analytische Lösung für Schwingungen des Euler-Bernoulli-Balkens beim Loslassen aus der enspannten Ruhelage.

tmp

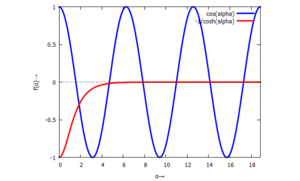
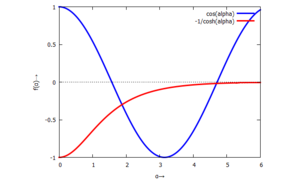
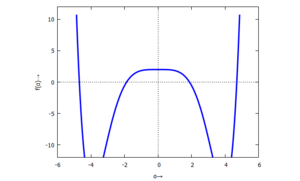
Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass

$E>0,I>0,{\ell }_0>0,\varrho >0;$.

Header

Text

📑 toggle code

1+1

tmp

In der Gleichgewichtsbeziehung für den Euler-Bernoulli-Balken setzen wir als eingeprägte, äußere Streckenlast q(x,t) die D'Alembert'sche Trägheitskraft und die Gewichtskraft an, also

$q(x,t)=\varrho A\cdot g-\varrho A\cdot \ddot{w}(x,t)$

Die Lösung der linearen, partielle Bewegungsgleichung

$\varrho A\cdot \ddot{w}+EI\cdot w^{IV}=\varrho A\cdot g$

setzt sich dann aus zwei Lösungsanteilen, der partikularen Lösung w_p und der homogenen Lösung w_h, zusammen; wir schreiben

$w_t(x,t)=w_p(x,t)+w_h(x,t)$.

Equations of Motion

Text

📑 toggle code

1+1

tmp

Die partikulare Lösung w_p erfüllt die "rechte Seite" der Bewegungsgleichung, also ϱ A⋅g:

$EI\cdot w_p^{IV}=\varrho A\cdot g$.

Die rechte Seite ist zeit-unveränderlich - so auch die partikulare Lösung.

Wir integrieren die Bewegungsgleichung vier Mal und erhalten

$EIw(x,t)=\frac{Ag\rho x^4}{24}+C_3\frac{x^3}{6}+C_2\frac{x^2}{2}+C_{1}x+C_0$.

Die vier Integrationskonstanten C_i müssen wir nun an die Randbedingungen

$\begin{array}{rl}{w}_p(0)& =0\\ {w_p}^{\prime }(0)& =0\\ EI{w_p}^{″}(\ell )& =0\\ EI{w_p}^{‴}(\ell )& =0\end{array}$

anpassen, wir erhalten mit dem linearen Gleichungssystem

$\begin{array}{l}0=C_0\\ 0=C_1\\ 0=\frac{{\ell }_0^{2}Ag\rho }{2}+{\ell }_0{C}_3+C_2\\ 0={\ell }_{0}Ag\rho +C_3\end{array}$

die partikulare Lösung

$EI{w}_p\left(x\right)=Ag\varrho {\ell }^4\cdot (\frac{{\xi }^4}{24}-\frac{{\xi }^3}{6}+\frac{{\xi }^2}{4})$

.

Statische Auslenkung

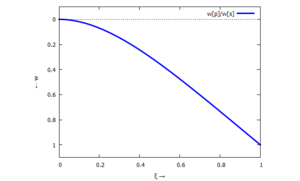
Die maximale Auslenkung - am rechten Rand - nutzen wir als Bezugslänge

$w_s=\frac{{\ell }^{4}Ag\rho }{8EI}$

Und so sieht w_p aus:

Particular Solution

Text

📑 toggle code

1+1

tmp

Homogeneous Solution

Text

📑 toggle code

1+1

tmp

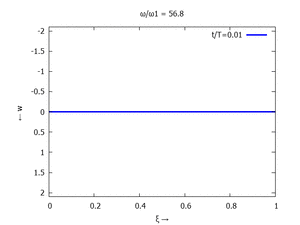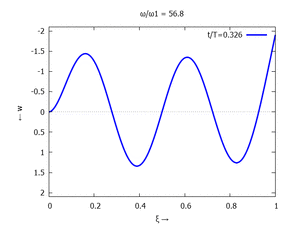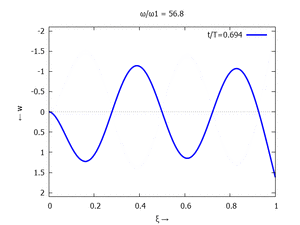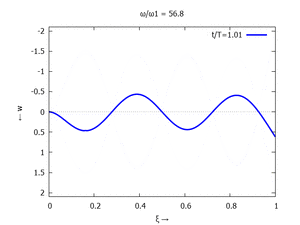
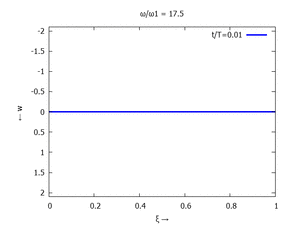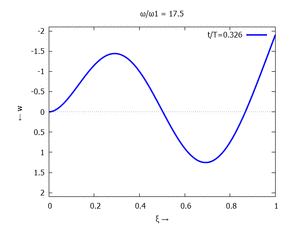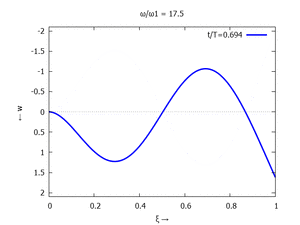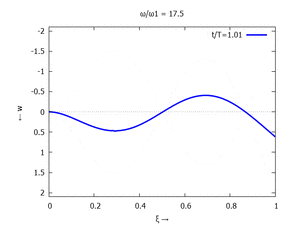
Adapt to Initial Condition

Text

📑 toggle code

1+1

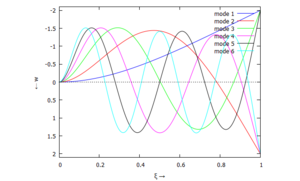
Mode	Modalform ϕj	Mode	Modalform ϕj
#1 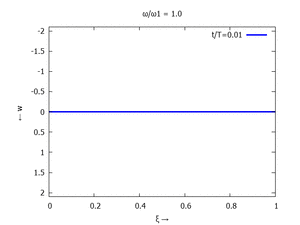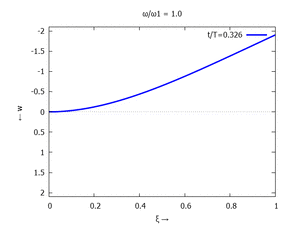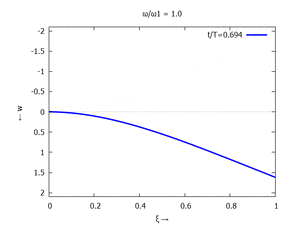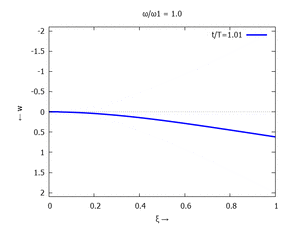$\omega$

---

Links

• ...

Literature

• ...

Animation: Loslassen des Systems aus der unverformten Rugelage.

Modalformen

Nullstellensuche

Nullstellensuche (Ausschnitt)

XXX

Animation: Loslassen des Systems aus der unverformten Rugelage.

Modalformen

Nullstellensuche

Nullstellensuche (Ausschnitt)

XXX

Statische Auslenkung

Lageplan

k