Gelöste Aufgaben/ODE1

Aufgabenstellung

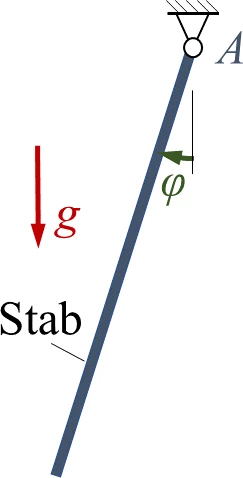
Hier untersuchen wir systematisch ein System aus einem starren Pendel im Erdschwerefeld.

Lageplan

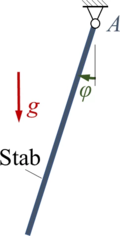
Gesucht sind Gleichgewichtslagen, Schwingungen um diese und die numerische Lösung der nichtlinearen Bewegungsgleichung.

Lösung mit Maxima

bzgl A ist J_A, der Schwerpunkt des Stabes liegt in seiner Mitte.

Header

Wir nehemn an: das Massenmoment des homogenen Stabes bzgl A ist JA, der Schwerpunkt des Stabes liegt in seiner Mitte.

/*******************************************************/ /* MAXIMA script */ /* version: wxMaxima 15.08.2 */ /* author: Andreas Baumgart */ /* last updated: */ /* ref: TM-C */ /* description: solve the IVP, check for stability */ /*******************************************************/

tmp

Aus dem Prinzip der virtuellen Verrückungen kommt die Gleichgewichtsbeziehung für den Stab:

$\delta W=\underset{=\delta W^a}{\underbrace{-J_A\cdot \ddot{\phi }\cdot \delta \phi -m\cdot g\cdot \frac{\ell }{2}\cdot \sin (\phi )\cdot \delta \phi }}-\underset{=\delta \mathrm{\Pi }}{\underbrace{0}}$,

wobei

$\phi =\phi (t)$

Mit der neuen, dimensionslosen Zeit

$\tau =\frac{t}{t_{Bez}}\text{ und }{t}_{Bez}^2=\frac{J_A}{m\cdot g\cdot \frac{\ell }{2}}$

wird aus der Bewegungsgleichung

$\frac{d^2}{d{\tau }^2}(\phi )+\sin (\phi )=0$

Declarations

Text

1+1

tmp

Die Gleichung

$\frac{d^2}{d{\tau }^2}\phi =0$

ist erfüllt für

$\sin (\phi )\stackrel{!}{=}0\text{, also }\phi =0,\pi ,2\pi ,\dots$

Gleichgewichtslagen

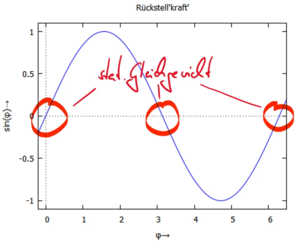
Die Funktion der Rückstell'kraft' sin(φ) schneidet die y-Achse dabei mit der Steigung +1 (z.B. bei φ₁ = 0, φ₃ = 2π) und mit der Steigung  -1 (z.B. bei φ₂ = π).

Das Vorzeichen der Steigung wird über die Stabilität der Lösung entscheiden!

Equilibrium Conditions

Text

1+1

tmp

Equilibrium Conditions and Stability

Text

1+1

tmp

Solving

Text

1+1

tmp

Post-Processing

Text

1+1

Phasendiagramm

Lösung im Zeitbereich

Lösung im Zeitbereich.

Lösung im Zeitbereich

---

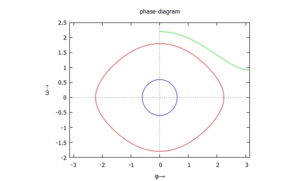
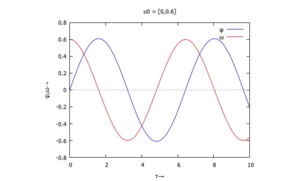
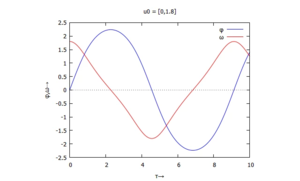
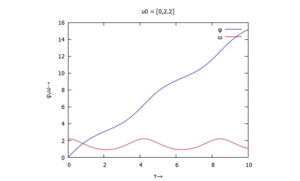
Links

• ...

Literature

• ...