Gelöste Aufgaben/LM01

Aufgabenstellung

Wie Minimum-Prinzipe "funktionieren" und wie die Mathematik dazu aussieht, untersuchen wir hier an einem klassischen Beispiel.

Lageplan

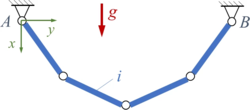
Gesucht ist die Lage der Knoten von vier starren Kettengliedern (Länge ℓ, Masse m) im Erdschwerefeld.

Lösung mit Maxima

Die Aufgabe ist ein einfaches Beispiel für Lösungsansätze mit "Lagrange-Multiplikatoren".

Header

Wir arbeiten mit dem Prinzip vom Minimum der Potentiellen Energie - also dem Potential der Gewichtskraft der Kettenglieder. Besonders charmant - im Vergleich zu Ansätzen mit dem Kräfte-Gleichgewicht ist hier das "Wegfallen" der Schnittkräfte - die brauchen wir hier nicht explizit angeben.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 18.10.1                           */
/* author: Andreas Baumgart                            */
/* last updated: 2019-01-31                            */
/* ref: form of hanging chain                    */
/* description: finds the form of a hanging chain      */
/*              employing Lagrange Multiplyers         */
/*https://de.wikipedia.org/wiki/Lagrange-Multiplikator */
/*******************************************************/

Declarations

Koordinaten

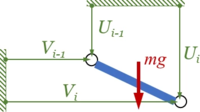
Jeder Verbindungspunkt eines Kettengliedes hat zwei Koordinaten U_j, V_j.

Die Arbeitsfunktion der Gewichtskraft ist

$\displaystyle A=\sum _{n=0}^{N}m\,g\,{\frac {U_{i-1}-U_{i}}{2}}$.

Im Gleichgewicht  hat diese Arbeitsfunktion ein Minimum, allerdings müssen dabei für die starren Kettenglieder die Bedingungen

$\left(U_{i}-U_{i-1}\right)^{2}+\left(V_{i}-V_{i-1}\right)^{2}=\ell ^{2}$

erfüllt sein!

/* declare variational variables - see 6.3 Identifiers */
declare("Λ", alphabetic);
declare("λ", alphabetic);
declare("γ", alphabetic);
declare("ℓ", alphabetic);

/* declarations */
params: [γ = m*g*ℓ];

/* number of chain elements */
N : 4;

Equilibrium Conditions

Die Lagrange-Funktion für die Kette lautet also

${\begin{array}{lll}\Lambda =&&\displaystyle \sum _{n=0}^{N}m\,g\,{\frac {U_{i-1}-U_{i}}{2}}\\&+&\displaystyle \sum _{n=0}^{N}\lambda _{i}\cdot \left(\left(U_{i}-U_{i-1}\right)^{2}+\left(V_{i}-V_{i-1}\right)^{2}-\ell ^{2}\right)\end{array}}$

mit den Lagrangeschen Multiplikatoren λ_i.

Hier ist N =4, die Randbedingungen für die Verschiebungen lauten also

$U_{0}=0,U_{4}=0,V_{0}=0{\text{ und }}V_{N}=L$

und wir wählen hier

$L=3\,\ell$.

Mit der Abkürzung

$\gamma =m\,g\,\ell$ und $U_{i}=\ell \;{\tilde {U}}_{i},\;\;V_{i}=\ell \;{\tilde {V}}_{i},$

ist dann

${\begin{array}{lll}\Lambda =&&\displaystyle {\frac {\left({{\tilde {U}}_{3}}+{{\tilde {U}}_{2}}\right)\gamma }{2}}+{\frac {{{\tilde {U}}_{3}}\gamma }{2}}+{\frac {\left({{\tilde {U}}_{2}}+{{\tilde {U}}_{1}}\right)\gamma }{2}}+{\frac {{{\tilde {U}}_{1}}\gamma }{2}}\\&+&\left({{\left(3-{{\tilde {V}}_{3}}\right)}^{2}}+{{\tilde {U}}_{3}^{2}}-1\right)\,{{\lambda }_{4}}\\&+&\left({{\left({{\tilde {V}}_{3}}-{{\tilde {V}}_{2}}\right)}^{2}}+{{\left({{\tilde {U}}_{3}}-{{\tilde {U}}_{2}}\right)}^{2}}-1\right)\,{{\lambda }_{3}}\\&+&\left({{\left({{\tilde {V}}_{2}}-{{\tilde {V}}_{1}}\right)}^{2}}+{{\left({{\tilde {U}}_{2}}-{{\tilde {U}}_{1}}\right)}^{2}}-1\right)\,{{\lambda }_{2}}\\&+&\left({{\tilde {V}}_{1}^{2}}+{{\tilde {U}}_{1}^{2}}-1\right)\,{{\lambda }_{1}}\end{array}}$.

Die Gleichgewichtsbedingungen unter Nebenbedingungen lauten dann

${\begin{array}{ll}\displaystyle {\frac {\partial \Lambda }{\partial U_{i}}}&=0\\\displaystyle {\frac {\partial \Lambda }{\partial V_{i}}}&=0\\\displaystyle {\frac {\partial \Lambda }{\partial \lambda _{i}}}&=0\end{array}}$.

/* equilibrium condition */
LagrangeFkt : Λ = sum(γ*(U[n-1]+U[n])/2,n,1,N)
                 +sum(λ[n]*((U[n]-U[n-1])^2+(V[n]-V[n-1])^2 - 1^2),n,1,N);

/* boundary conditions */
BCs : [U[0]=0, V[0]=0, U[N]=0, V[N]=N-1]$
/* unknowns (nodal coordiantes and Lagrange-multiplyers )*/
Q : flatten(append(makelist([U[n],V[n],λ[n]],n,1,N-1),[λ[N]]))$

LagrangeFkt : expand(subst(BCs,LagrangeFkt))$

equ : makelist(diff(subst(LagrangeFkt,Λ),Q[i]),i,1,3*(N+1)-4-1)$
equ : subst([γ = 1],equ);

Solving

Die Gleichungen, die wir nun lösen müssen sind:

${\begin{array}{ll}0=&-2{{\tilde {U}}_{2}}\,{{\lambda }_{2}}+2{{\tilde {U}}_{1}}\,{{\lambda }_{2}}+2{{\tilde {U}}_{1}}\,{{\lambda }_{1}}+1\\0=&-2{{\tilde {V}}_{2}}\,{{\lambda }_{2}}+2{{\tilde {V}}_{1}}\,{{\lambda }_{2}}+2{{\tilde {V}}_{1}}\,{{\lambda }_{1}}\\0=&{{\tilde {V}}_{1}^{2}}+{{\tilde {U}}_{1}^{2}}-1\\0=&-2{{\tilde {U}}_{3}}\,{{\lambda }_{3}}+2{{\tilde {U}}_{2}}\,{{\lambda }_{3}}+2{{\tilde {U}}_{2}}\,{{\lambda }_{2}}-2{{\tilde {U}}_{1}}\,{{\lambda }_{2}}+1\\0=&-2{{\tilde {V}}_{3}}\,{{\lambda }_{3}}+2{{\tilde {V}}_{2}}\,{{\lambda }_{3}}+2{{\tilde {V}}_{2}}\,{{\lambda }_{2}}-2{{\tilde {V}}_{1}}\,{{\lambda }_{2}}\\0=&{{\tilde {V}}_{2}^{2}}-2{{\tilde {V}}_{1}}\,{{\tilde {V}}_{2}}+{{\tilde {U}}_{2}^{2}}-2{{\tilde {U}}_{1}}\,{{\tilde {U}}_{2}}+{{\tilde {V}}_{1}^{2}}+{{\tilde {U}}_{1}^{2}}-1\\0=&2{{\tilde {U}}_{3}}\,{{\lambda }_{4}}+2{{\tilde {U}}_{3}}\,{{\lambda }_{3}}-2{{\tilde {U}}_{2}}\,{{\lambda }_{3}}+1\\0=&2{{\tilde {V}}_{3}}\,{{\lambda }_{4}}-6{{\lambda }_{4}}+2{{\tilde {V}}_{3}}\,{{\lambda }_{3}}-2{{\tilde {V}}_{2}}\,{{\lambda }_{3}}\\0=&{{\tilde {V}}_{3}^{2}}-2{{\tilde {V}}_{2}}\,{{\tilde {V}}_{3}}+{{\tilde {U}}_{3}^{2}}-2{{\tilde {U}}_{2}}\,{{\tilde {U}}_{3}}+{{\tilde {V}}_{2}^{2}}+{{\tilde {U}}_{2}^{2}}-1\\0=&{{\tilde {V}}_{3}^{2}}-6{{\tilde {V}}_{3}}+{{\tilde {U}}_{3}^{2}}+8\end{array}}$.

Und die sind nichtlinear! Dafür brauchen wir eine Lösungsroutine - wir verwenden das Newton–Verfahren.

Wir finden:

${\begin{array}{lll}{{\tilde {U}}_{1}}=&&0.807\\{{\tilde {V}}_{1}}=&&0.59\\{{\lambda }_{1}}=&-&0.929\\{{\tilde {U}}_{2}}=&&1.22\\{{\tilde {V}}_{2}}=&&1.5\\{{\lambda }_{2}}=&-&0.603\\{{\tilde {U}}_{3}}=&&0.807\\{{\tilde {V}}_{3}}=&&2.41\\{{\lambda }_{3}}=&-&0.603\\{{\lambda }_{4}}=&-&0.929\end{array}}$.

✔ Lösungen nichtlinearer Gleichungen:

... sind eine Wissenschaft für sich. Selbst für scheinbar triviale Probleme wie dieses laufen wir für N>4 schon in große numerische Probleme hinein. Der Trick ist häufig, als Startpunkt der Iteration Werte vorzugeben, die einigermaßen in der Nähe der erwarteten Lösung liegen. Sonst verabschiedet sich der Newton-Algorithmus oft mit einem "convergance error". Oder wir finden Lösungen, die zwar Gleichgewichtsbedingungen sind aber offensichtlich instabil sind.

/* solve nonlinear equations */
/* make shure, the Jabian ist not zero for the choice of "start" */
/* iteration starts with ..... */
start : makelist(1+i/length(Q),i,1,length(Q))$
load ("mnewton")$
/* iteration controls */
newtonmaxiter: 300;
newtonepsilon: 0.0001;
/* solve */
sol: mnewton(equ,Q,start)[1];

Post-Processing

Lösungskonstellation

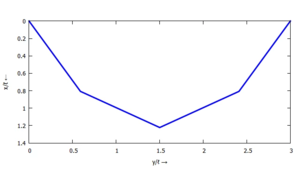
Hier erhalten wir jedoch eine Lösung - und so sieht sie aus;

/* post-processing */
/* plot solutions */
preamble: "set yrange [] reverse";

plot2d (subst(sol,subst(BCs,[discrete, makelist(V[i],i,0,N),makelist(U[i],i,0,N)])),
  [gnuplot_preamble, preamble], same_xy,
  [style, [lines,3]],
  [xlabel, "y/ℓ →"],
  [ylabel, "x/ℓ ←"] )$

---

Links

• ...

Literature

• ...