Gelöste Aufgaben/Kw27

Aufgabenstellung

Scheibenwischer können auf einer Windschutzscheibe laute "Rubbel"-Geräusche erzeugen - eine Bewegung, die sich selbsterregt aus dem Zusammenspiel eines schwingungsfähigen Systems und einer Reibkennlinie ergibt.

Scheibenwischer-"Rubbeln"

Für ein einfaches Ersatz-System modellieren wir den Wischer-Arm als zwei parallele, masselose Blatt-Federn (Euler-Bernoulli-Balken mit Biegesteifigkeit jeweils EI₁ und EI₂ bzgl der Auslenkung senkrecht zur Scheibe und tangential dazu) und idealisieren das Wischerblatt durch eine Punktmasse (Masse m). Zwischen der Lippe des Scheibenwischers und der Windschutzscheibe wirkt eine Tangentialkraft aus trockener Reibung (μ, μ₀).

Wischerblatt auf Scheibe.

Gesucht ist die selbsterregte Schwingung des Wischerblatts beim "Rubbeln" auf der Windschutzscheibe. Simulieren Sie dazu "Stick-Slip"-Schwingungen des Systems.

Lösung mit Maxima

Header

"Stick-Slip" Schwingungen sind klassische selbsterregte Schwingungen. Selbsterrung heißt: das System lenkt den Energiefluss im System so, dass Schwingungen "aus sich heraus" angeregt werden. Charakteristisch für "Stick-Slip" Schwingungen ist, dass zwei Körper zeitweise aneinander haften, auseinander gerissen werden und dann aneinander reiben - bis sie wieder aneinander haften.

📑 toggle code

/*********************************************************/
/* MAXIMA script                                         */
/* version: wxMaxima 15.08.2                             */
/* author: Andreas Baumgart                              */
/* last updated: 2018-09-28                              */
/* ref: Kw27 (TM-C, Labor 6)                             */
/* description: finds the solution for                   */
/*              the nonlinear IVP of                     */
/*              windshield wiper rubbing                 */
/*********************************************************/

Declarations

Lageplan

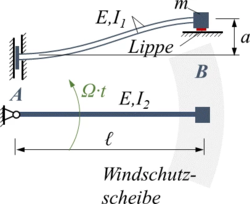
Im Zentrum dieser Aufgabe steht die Kennlinie (engl.: Characteristic), die den Zusammenhang zwischen Tangentialkräft (Haftkraft, Reibkraft), Normalkraft und Relativgeschwindigkeit zwischen Wischer-Lippe und Windschutzscheibe erfasst.

Trockene Reibung im Modell beschreibt man mit zwei System-Parametern:

• dem Reibungskoeffizient μ und
• dem Haftungskoeffizient μ₀.

und es gilt

• 'μ₀' >μ.

Wir arbeiten mit dem Ersatz-System rechts:

📑 toggle code

/*********************************************************/
/* declarations */
assume(mu[0]>0,mu[1]>0,mu[0]>mu[1]);

Friction Characteristic

Reibkennlinie

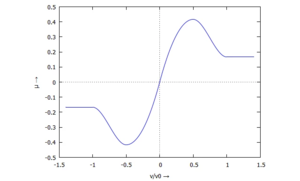
Die Kennlinie für die Reibkraft

$R=N\cdot \mu (v_r)$

kopieren wir mit der Funktion für den den Reibungskoeffizienten

$\mu (v_r)\text{ in Abhängigkeit von der Relativgeschwindigkeit }{v}_r$

aus Abschnitt Reibkennlinie stückweise mit Polynomen 2ten und 3ten Grades zu

$\mu (v_r)=\{\begin{array}{ll}+\mu & \text{ für }+1<\nu \\ 16\cdot {\mu }_0(1-\frac{{\mu }_1}{{\mu }_0})\cdot {\nu }^3-36\cdot {\mu }_0(1-\frac{{\mu }_1}{{\mu }_0})\cdot {\nu }^2+24\cdot {\mu }_0(1-\frac{{\mu }_1}{{\mu }_0})\cdot \nu +5\cdot {\mu }_1-4\cdot {\mu }_0& \text{ für }+\frac{1}{2}<\nu <=+1\\ 4\cdot {\mu }_0\cdot (\nu -{\nu }^2)& \text{ für }0<\nu <=+\frac{1}{2}\\ \text{und punktsymmetrisch}& \text{ sonst}\end{array}$

Sie muss punkt-symmetrisch sein (die Reibkraft ändert ihr Vorzeichen mit der Orientierung der Relativgeschwindigkeit) und sie enthält den Sonderfall "Haften" für

$-ϵ<v_r<+ϵ$

📑 toggle code

/*****************************************************/
/* declarations from Lexikon Section "Reibkennlinie" */
/**** define nonlinear friction characteristic     ***/
fric(nu, mu) := 
  if nu < -1 then
     /* section III, neg.*/
     -mu[2]
  elseif nu < -1/2 then
     /* section II, neg.*/   
     (16*mu[1]-16*mu[2])*nu^3-(36*mu[2]-36*mu[1])*nu^2+(24*mu[1]-24*mu[2])*nu-5*mu[2]+4*mu[1]
  elseif nu < 0 then
     /* section I, neg.*/
     4*mu[1]*nu+4*mu[1]*nu^2
  elseif nu < +1/2 then
     /* section I, pos.*/
     4*mu[1]*nu-4*mu[1]*nu^2
  elseif nu < +1 then
     /* section II, pos.*/
     (16*mu[1]-16*mu[2])*nu^3+(36*mu[2]-36*mu[1])*nu^2+(24*mu[1]-24*mu[2])*nu+5*mu[2]-4*mu[1]
  else
     mu[2] /* section III, pos.*/
     ;
plot2d([discrete,makelist([i/100,fric(i/100,[5/12, 2/12])],i,-140,+140)],[xlabel,"v/v0 →"], [ylabel,"μ →"]);

Equilibrium Conditions

Zwei Gleichgewichtsbedingungen brauchen wir:

1. für die Normalkraft N und
2. die Bewegungsgleichung der Masse m.

Normalkraft N

Die Normalkraft N erhalten wir aus den Standard-Lösungen bzw. deren Ersatzfeder-Steifigkeiten für den Euler-Bernoulli-Balken zu

$N=2\cdot \frac{12\cdot E{I}_1}{{\ell }^3}\cdot a$.

Koordinaten

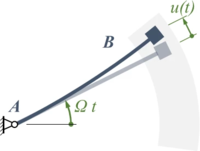
Für die Bewegungsgleichung des Systems wählen wir als Koordinaten die elastische Verformung des Wischer-Arms in B, positiv in Richtung der Drehbewegung. Wir gehen davon aus, dass der Wischer in A mit der konstanten Geschwindigkeit Ω gedreht wird, die Punktmasse m also den Weg

$s(t)=\mathrm{\Omega }t\ell +u(t)$

zurücklegt.  

Kräftegleichgewicht

Aus dem Kräftegleichgewicht an der Masse schreiben wir (mit dem Prinzip von d'Alembert)

$m\ddot{u}+F_2+R=0$

an.

Die Kennlinie für die Reibkraft R haben wir dafür oben schon festgelegt.

Die Rückstellkraft F₂ der beiden Blattfedern ist

$\begin{array}{l}{F}_2:=k\cdot u\end{array}$

mit

$k=2\cdot \frac{3E{I}_2}{{\ell }^3}$.

Dimensionslos machen wir die Bewegungsgleichung mit

• der Referenzzeit T aus der Eigenkreisfrequenz des Wischerblattes ohne Reibung zu
  $\begin{array}{ll}{\omega }_0& =2\pi /T\\ & =\sqrt{k/m}\end{array}$ mit der Eigenkreisfrequenz ${\omega }_0$ des frei schwingenden Körpers (R=0) und
• der Referenz-Länge $\ell$.
</ul Dann ist die dimensionslose Auslenkung U = u/ℓ und die dimensionslose Zeit τ = t/T. Entsprechend gilt auch

$\frac{d}{dt}(.)=\frac{1}{T}\frac{d}{d\tau }(.)$

Einsetzten liefert die Bewegungsgleichung

$\frac{d^{2}U}{d{\tau }^2}+4{\pi }^2\cdot U+16{\pi }^2\alpha \gamma \cdot \mu (v_r)=0$

mit

$\alpha =\frac{a}{\ell },\gamma =\frac{E{I}_1}{E{I}_2}$.

📑 toggle code




/***************************************/
/* compute press-down force N          */
press: solve([N       = 2*F,
              EI[1]*a = F*l^3/3+M*l^2/2,
              EI[1]*Phi[B] = 1/2*F*l^2+M*l,
              Phi[B]  = 0], [N, F, M, Phi[B]])[1];

/* define ODE in dim'less coordinate U */
params : [k     = 2*3*EI[2]/l^3,
          EI[1] = gamma*EI[2],
          a     = alpha*l];
eom : m*'diff(u,t,2) + k*u + R = 0;

fstOrd : ['diff(U,tau,2)='diff(V,tau,1)];
ref    : [solve((2*%pi/T)^2 = k/m,T)[2]];
dimless: [t = tau*T, v = V*l/T,
          v0 = l*Omega*epsilon,
          Omega =  2*%pi/(Theta*T)];

/* Estimate for Theta:               */
/* Theta = Rubbel-Frequ./ Dreh-Frequ */
/*       = 100Hz/1Hz                  */
/*************************************/

eom : expand(ratsimp(
    subst(['diff((l*U),tau,2)=l*'diff(U,tau,2)],
      subst(ref,subst(['diff(u,t,2) = 'diff(u,tau,2)/T^2, u = l*U],
          4*%pi^2/(k*l)*eom)))));

eom : subst(params,subst([R=subst(press,N)*fric(ratsimp(subst(dimless,(l*Omega+v)/v0)),mu)],eom));

eom : [subst(fstOrd,eom), 'diff(U,tau,1)=V];
dydt : solve(eom,['diff(V,tau,1),'diff(U,tau,1)])[1];










Solving

Für die numerische Lösung transformieren wir auf eine Differentialgleichung erster Ordnung

$\begin{array}{ll}\frac{dU}{d\tau }& =V,\\ \frac{dV}{d\tau }& =-4\cdot {\pi }^2\cdot (U+4\alpha \gamma \cdot \mu \left(v_r\right))\end{array}$

die wir als Anfangswertproblem

$\underset{\_}{\dot{q}}=\underset{\_}{f}(\underset{\_}{q})$

mit

$\underset{\_}{q}=\left(\begin{array}{c}U\\ V\end{array}\right)$

lösen. Als Anfangsbedingungen wählen wir zwei aus, nämlich

${\underset{\_}{q}}_{0,1}=\left(\begin{array}{l}0\\ 0\end{array}\right)$ und ${\underset{\_}{q}}_{0,2}=\left(\begin{array}{c}0\\ -\frac{\pi }{50}\end{array}\right)$.

Als zweite Anfangsbedingung haben wir dabei das V so gewählt, dass die Relativgeschwindigkeit zwischen Lippe und Scheibe gerade Null ist, also

$\mathrm{\Omega }\ell +\dot{u}=0$

gilt.

📑 toggle code




/*********************************************************/
/* numerical solution of IVP */
/* numerical parameters      */		
numpars: [alpha  = 1/100,
          gamma  = 10,
          Theta  = 100,
          epsilon= 1/10000,
          mu[1]  = 10/12, mu[2]=5/12];

/* reminder:
          EI[1] = gamma*EI[2],
          a     = alpha*l];
          v0    = l*Omega*epsilon,
          Omega =  2*%pi/(Theta*T) */

numpars: [alpha  = 1/100,
          gamma  = 2,
          Theta  = 100,
          epsilon= 1/1000,
          mu[1]  = 5/12, mu[2]=2/12];
/* write out results at these times */
times : subst([t0 = 0, tmax = 5, dt = 0.001],
                    [t, t0, tmax, dt]);

/* first-order dgl */
dgl1stOrder : [rhs(dydt[2]),float(subst(numpars,rhs(dydt[1])))];
/* state variables */
stateVabs : [U,V];
/* initial values for state variables */
initiVals : [[0,0],
             /*initial absolute speed = 0 */
             [0,subst(numpars,subst(solve(subst(dimless,Omega*l+v=0),V),V))]];

/* solve: solution of IVP (ivs) */
for i: 1 thru length(initiVals) do
   ivs[i] : rk(dgl1stOrder, stateVabs, initiVals[i], times)$










Post-Processing

Für die zwei Anfangsbedingungen finden wir diese Auslenkungen U(τ):



Phasendiagramm

Unabhängig von den Anfangsbedingungen läuft das System sofort in die "Stick-Slip" Schwingung hinein.

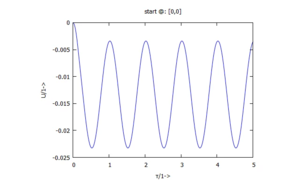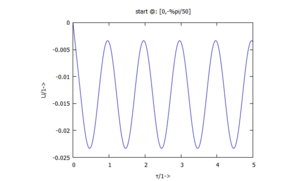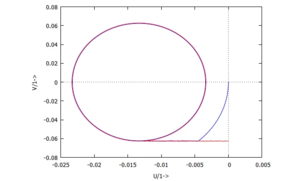
Hier erkennt man gut, wie die Lippe am der Scheibe haften bleibt - für V=-π/50 sind Band und Körper-Geschwindigkeit gleich.

📑 toggle code




/*********************************************************/
/* plot results */
for i: 1 thru length(initiVals) do
	(T[i] : makelist(ivs[i][j][1],j,1,length(ivs[i])),
	 uD[i] : makelist(ivs[i][j][2],j,1,length(ivs[i])),
	 vD[i] : makelist(ivs[i][j][3],j,1,length(ivs[i])),
	 plot2d([discrete, T[i], uD[i]],
	      [title, sconcat("start @: ",string(initiVals[i]))],
	                   [xlabel,"τ/1->"], [ylabel,"U/1->"]));

/* phase plot */
curves : makelist([discrete,uD[i],vD[i]],i,1,length(initiVals))$
plot2d(curves, [legend, false], [x,-0.025,0.005],
                   [ylabel,"V/1->"], [xlabel,"U/1->"]);










✔ Problem gelöst?:

Das Modell ist so einfach, dass man schnell den Einfluss von Steifigkeiten (was passiert, wenn ich die Eigenfrequenz des Systems erhöhe?) herausspielen kann. Das ist gut. Wischer-Blatt im Schnitt Es ist aber auch so einfach, dass zentrale Charakteristika nicht erfasst werden. So sieht ein Wischer-Blatt im Schnitt ungefähr so aus. Es legt sich im Betrieb seitlich auf die Windschutzscheibe, Außerdem sind die Wischer-Arme in der Regel keine geraden "Biegebalken", so dass sie sich bei Vor- und Rückbewegung anders verhalten. Auch vermute ich, dass eine Bewegung senkrecht zur Windschutzscheibe eine Rolle spielt: die Lippe "klopft" vermutlich auf die Scheibe. Trotzdem würde man so anfangen: ein ganz einfaches Modell für den Einstieg, das man dann weiter entwickelt.




---

Links

• ...

Literature

• ...