Gelöste Aufgaben/Kw24
Aufgabenstellung
Ein Mechanismus besteht aus einem starren Stab AC (Länge ℓ1, Massenmoment J) und einer Feder BC (Länge ℓ2 im entspannten Zustand, Steifigkeit k).
Die Körper sind drehbar gelagert, der Abstand AB ist ℓ3.
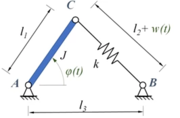
Hier geht es um die verschiedenen Lösungstypen des Systems - in Abhängigkeit von den Anfangsbedingungen. Gesucht sind Lösungen als Anfangswertproblem, nichtlineare Schwingungen und Aussagen über die Stabilität der Bewegungen.
Lösung mit Maxima
Header
Gesucht ist die Lösung zu dem nichtlinearen Anfangswertproblem.
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-09-30 */
/* ref: Kw24 (TM-C, Labor 6) */
/* description: finds the solution for */
/* the nonlinear IVP */
/*********************************************************/
Declarations
Wir wählen die Längenverhältnisse
so dass die Feder für φ(t) = 45° entspannt ist.
/*********************************************************/
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic); /* total virtual work */
declare( "φ", alphabetic); /* coordinate of rotatin */
declare("δφ", alphabetic); /* variation of coordinate phi*/
declare("δw", alphabetic); /* variation of coordinate w */
/* parameter */
assume(l[1]>0, k>0, J>0);
params: [l[2] = l[1], l[3] = sqrt(2)*l[1]];
Kinematics
Der Mechanismus hat genau einen Freiheitsgrad, den wir entweder durch die Federlängung w oder den Drehwinkel φ erfassen. Den Zusammen zwischen den beiden stellen wir über
her. Nun steht uns frei, ob wir diese Beziehung nach w oder φ auflösen. Wir wählen φ als Minimal-Koordinate und erhalten
Nach den Regeln der Variationsmethoden erhalten wir daraus:
- .
/*********************************************************/
/**** kinematics ***/
/* coordinates */
coords : [φ, δφ];
kin : (l[1]*sin(φ(t)))^2+(l[3]-l[1]*cos(φ(t)))^2=(l[2]+w)^2;
kin : trigsimp(ratsimp(solve(subst(params, kin),w)[2]));
kin : [kin,
δw = subst([epsilon=0],
diff(subst([φ(t)=φ(t)+epsilon*δφ],
subst(kin,w)),epsilon))];
Equilibrium Conditions
Mit dem Prinzip der virtuellen Verrückungen schreiben wir
und erhalten die Bewegungsgleichung
/*********************************************************/
/* equilibrium conditions */
PvV : δW = -J*'diff(φ(t),t,2)*δφ - k*w*δw;
/* dgl for φ ist the coefficient of δφ in δW */
dgl[1] : expand(coeff(subst([δW = 0], subst(kin, -PvV)),δφ));
Equilibrium Points
Die Bewegungsgleichung machen wir dimensionslos, indem wir charakteristische Größen aus der linearisierten Bewegungsgleichung verwenden.
Die drei Gleichgewichts-Lagen bzgl. derer wir die Bewegungsgleichung linearisieren können, sind
- .
Eine Taylor-Reihenentwicklung des Rückstellmoments bzgl. φ0,3 ,also
liefert die linearisierte Bewegungsgleichung
- .
Dabei ist ω0 die Eigenkreisfreuquenz der linearisierten Bewegungsgleichung.
/*********************************************************/
/* Zeros of restoring function */
equilib : solve(subst(['diff(φ(t),t,2)=0],dgl[1]),φ(t));
/*********************************************************/
/* derive the eigenfrequency */
/* of linearized ODE at stable point of equilob. */
LinODE : taylor (subst([φ(t)=psi],rhs(dgl[1]/J)), psi, %pi/4,1);
ref : omega[0]^2 = coeff(expand(LinODE),psi);
ref : [t[B] = 1/(subst(solve(ref,omega[0])[2],omega[0])/(2*%pi))];
Make Equations of Motion Dimensionless
Eine Bezugszeit für unsere nichtlineare Bewegungsgleichung kommt nun aus
Damit lautet die dimensionslose Bewegungsgleichung
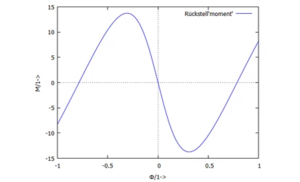
Den nichtlinearen (zweiten) Summand können wir als dimensionsloses "Rückstellmoment auffassen und über dem Drehwinkel auftragen:
Nullstellen des Rückstellmoments zeigen die Gleichgewichtslagen des Systems an. Die Steigung dieses Rückstellmoments in den Gleichgewichtslagen deutet dabei auf die Stabilität der linearisierten Bewegung (oder Bewegung im Kleinen) hin. So ist die Lösung Φ = 0 eine instabile Gleichgewichtslage, die beiden anderen sind stabil.
/*********************************************************/
/* make dgl dimensionless employing the eigenfrequency */
dgl[2] : subst([diff(φ(t),t,2) = 'diff(Phi,t,2)/t[B]^2,
φ(t) = Phi ] , dgl[1]);
dgl[2] : solve(subst(ref,dgl[2]), 'diff(Phi,t,2));
/* equilibrium angles für Φ */
plot2d(-rhs(dgl[2][1]), [Phi,-1,1],
[legend, "Rückstell'moment'"],
[xlabel, "Φ/1->"], [ylabel, "M/1->"]);
Numerical Solution
Für die numerische Lösung müssen wir die Bewegungsgleichung
umschreiben auf eine Differentialgleichung erster Ordnung:
Diese lösen wir mit einer fertigen Routine - hier einem Runge-Kutta-Verfahren - als Anfangswertproblem. Anders als bei linearisierten Bewegungsgleichungen hängt die Charakteristik der Lösung von den Anfangsbedingungen ab.
/*********************************************************/
/* numerical solution of IVP */
fpprintprec:3$
lhs(dgl[2][1]) = float(expand(rhs(dgl[2][1])));
times : subst([t0 = 0, tmax = 6, dt = 0.01],
[t, t0, tmax, dt]);
dgl1stOrder : [Omega,float(expand(rhs(dgl[2][1])))];
stateVabs : [Phi,Omega];
initiVals : [[1,0],[-1,0],
[0,0.001],[0,3],
[0,8], [0,10]];
/* solution of IVP (ivs) */
for i: 1 thru length(initiVals) do
ivs[i] : rk(dgl1stOrder, stateVabs, initiVals[i], times)$
tmp
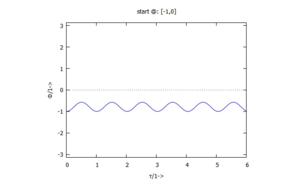
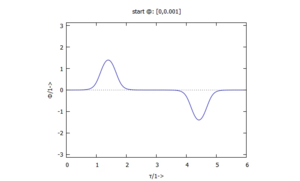
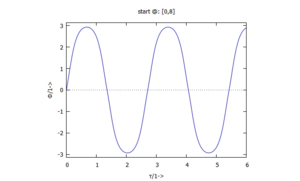
Das schauen wir uns am Verlauf von Lösungen im Zeitbereich an:
a)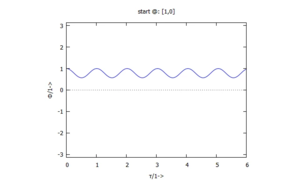
| 
b) |
c) | 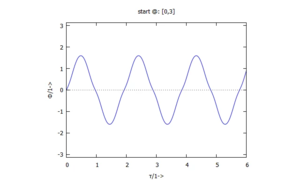
d) |
e) | 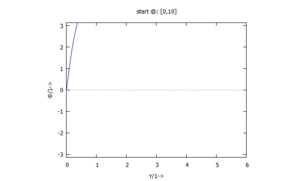
f) |
Lösung f) fällt aus dem Raster - hier gibt es keine periodische Lösung mehr: Bei einer anderen Skalierung der Φ-Achse erkennen wir, dass der Stab AC um den Punkt A rotiert:
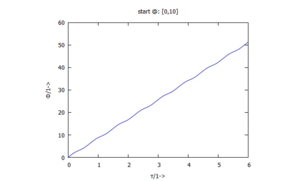
Oft erkennt man das Charakteristische einer Lösung im Phasendiagramm. Hier wird die Geschwindigkeit Ω über dem Drehwinkel Φ aufgetragen:
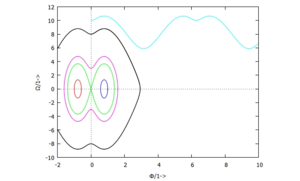
Periodische Lösungen - die oft gesucht sind - erkennt man an einem geschlossenen Verlauf. Die hellblaue Lösung gehört zu den Anfangswerten von f), bei dem der Drehwinkel immer größer wird - sich also keine periodische Lösung ergibt.
Wir sehen, dass die Lösung e) (schwarz) eine "gerade noch" periodische Lösung ist - etwas mehr Anfangsgeschwindigkeit im System und die Lösung sieht wie in f) aus. Diese Lösung nennt man auch Separatrix - sie separiert zwei Charakteristiken von Lösungen.
Analog sehen Sie in der Lösung c) (grün) eine Separatrix zwischen der periodischen Lösung der kleinen Schwingung um die Gleichgewichtslage und solchen periodischen Lösungen, bei denen der Stab die Horizontale durchbricht:
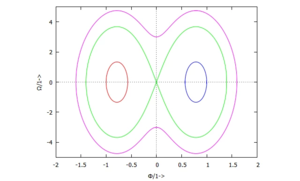
Post-Processing
Text
/*********************************************************/
/* plot results */
for i: 1 thru length(initiVals) do
(T[i] : makelist(ivs[i][j][1],j,1,length(ivs[i])),
P[i] : makelist(ivs[i][j][2],j,1,length(ivs[i])),
O[i] : makelist(ivs[i][j][3],j,1,length(ivs[i])),
plot2d([discrete, T[i], P[i]], [y,-%pi,%pi],
[title, sconcat("start @: ",string(initiVals[i]))],
[xlabel,"τ/1->"], [ylabel,"Φ/1->"]));
/* phase plot */
curves : makelist([discrete,P[i],O[i]],i,1,length(initiVals))$
plot2d(curves, [legend, false], [x,-2,10],
[ylabel,"Ω/1->"], [xlabel,"Φ/1->"]);
plot2d(curves, [legend, false], [x,-2,2], [y,-5,5],
[ylabel,"Ω/1->"], [xlabel,"Φ/1->"]);
plot2d(curves, [legend, false], [x,-2,2], [y,-5,5], [svg_file, "Kw24-20.svg"],
[ylabel,"Ω/1->"], [xlabel,"Φ/1->"]);
Links
- ...
Literature
- ...