Gelöste Aufgaben/Hko8

Aufgabenstellung

Lageplan

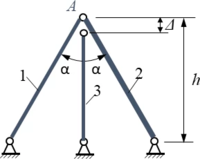
Drei Stäbe 1, 2 und 3 werden in Punkt A verbunden. Aufgrund einer Fertigungstoleranz ist Stab 3 um zu kurz. Gesucht ist die Verschiebung des Punktes A nach dem Einhängen von Stab 3 sowie die Spannungen in den Stäben. Die drei Stäbe haben die Querschnittsfächen

$A_1;A_2=2A_1,A_3=A_1$

und die Abmessungen

$h,\mathrm{\Delta },\alpha =30^{\circ }$

Alle Stäbe sind aus dem gleichen Material mit E-Modul E:

Lösung mit Maxima

... nach dem Prinzip vom Minimum der potentiellen Energie:

• "Das System ist im Gleichgewicht, wenn die Potentielle Energie des Systems ein Minimum hat."

Header

Wir arbeiten mit wxMaxima 15.08.2.

📑 toggle code

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2017-02-28                            */
/* ref: Mathe 2                                        */
/* description: Dehnstäbe verspannt eingebaut          */
/*                                                     */
/*******************************************************/

Declarations

Parameter:

$a=\tan \left(\alpha \right)\cdot h,\alpha =\frac{\pi }{6},A_3=A_1,A_2=2\cdot A_1$

📑 toggle code

/*******************************************************/
assume(a>0, h>0);
par : [a = h*tan(alpha), alpha = %pi/6, A[3]=A[1], A[2]=2*A[1]];

Kinematics

Freischnitt: Knoten A

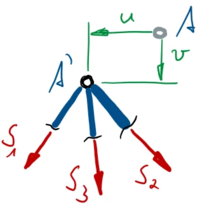
Aus dem Satz des Pythagoras kommt:

$\begin{array}{l}{({\mathrm{\Delta }}_1+l_1)}^2={(h-v)}^2+{(a-u)}^2\\ {({\mathrm{\Delta }}_3+l_3)}^2={(h-\mathrm{\Delta }-v)}^2+u^2\\ {({\mathrm{\Delta }}_2+l_2)}^2={(h-v)}^2+{(a+u)}^2\end{array}$

📑 toggle code

/*******************************************************/
length : [(l[1]+Delta[1])^2 = (h      -v)^2+(a-u)^2,
          (l[3]+Delta[3])^2 = (h-elta-v)^2+(  u)^2,
          (l[2]+Delta[2])^2 = (h      -v)^2+(a+u)^2];
diff  : makelist(Delta[i],i,1,3);
null : append([u=0, v=0], makelist(Delta[i]=0,i,1,3));
length : subst(par,length);
L[0] : subst(par,solve(subst(null,length), makelist(l[i],i,1,3)))[5];
L[1] : expand(subst(L[0],subst([delta=0],length)));

Linearize for small deflections

Die Stab-Längung linearisieren wir bezüglich der Koordinaten u, v und erhalten

Dehnungen:

${\epsilon }_1=-\frac{\sqrt{3}\cdot (u+\sqrt{3}\cdot v)}{4\cdot h},{\epsilon }_2=\frac{\sqrt{3}\cdot (u-\sqrt{3}\cdot v)}{4\cdot h},{\epsilon }_3=\frac{-v+\mathrm{\Delta }+\text{...}}{h-\mathrm{\Delta }}$

Spannungen:

${\sigma }_1=-\frac{\sqrt{3}\cdot (u+\sqrt{3}\cdot v)\cdot E}{4\cdot h},{\sigma }_2=\frac{\sqrt{3}\cdot (u-\sqrt{3}\cdot v)\cdot E}{4\cdot h},{\sigma }_3=\frac{(-v+\mathrm{\Delta }+\text{...})\cdot E}{h-\mathrm{\Delta }}$

📑 toggle code

/*******************************************************/
/* Linearisieren */
/* entweder .... */
L[2] : trunc(taylor(solve(L[1],diff),[u,v],0,1)[2]);
/* oder .... */
small : [u,v,Delta[1],Delta[2],Delta[3], delta];
L[3] : solve(subst([nu=1],subst([nu^2=0], subst(makelist(small[i] = nu*small[i],i,1,length(small)),L[1]))),diff)[1];

Epsilon : subst(L[2],subst(L[0], makelist(epsilon[i] = Delta[i]/l[i],i,1,3)));
Sigma   : makelist(sigma[i] = subst(Epsilon,E*epsilon[i]),i,1,3);

Equilibrium Conditions

U hat ein Minimum (Extremwert), wenn

$\frac{dU}{du}\stackrel{!}{=}0\text{ und }\frac{dU}{dv}\stackrel{!}{=}0$

wobei die Potentielle Energie im System

$U=\sum _{i=1}^3{U}_i\text{ mit }{U}_i=\underset{{\ell }_i}{\int }\frac{1}{2}{\sigma }_i\cdot {\epsilon }_{i}dx$

ist und damit

$U=\frac{\sqrt{3}\cdot A_1\cdot {(u+\sqrt{3}\cdot v)}^2\cdot E}{8\cdot h}+\frac{\sqrt{3}\cdot A_1\cdot {(u-\sqrt{3}\cdot v)}^2\cdot E}{4\cdot h}+\frac{A_1\cdot {(-v+\mathrm{\Delta }+\text{...})}^2\cdot E}{h}$.

📑 toggle code

/*******************************************************/
U : sum(subst(par, A[i]*subst(Epsilon,subst(Sigma, subst(L[0],sigma[i]*epsilon[i]*l[i])))),i,1,3);
U : subst([h-delta=h],U);

Solving

Auflösen des Gleichungssystems liefert:

$\begin{array}{l}u=-\frac{\sqrt{3}-3}{6}\cdot \mathrm{\Delta },\\ v=\frac{\sqrt{3}-1}{2}\cdot \mathrm{\Delta }\end{array}$

Die Stab-Kräfte erhalten wir entsprechend zu

$\begin{array}{l}{S}_1=-\frac{(\sqrt{3}-1)\cdot A_1\cdot E}{2\cdot h}\cdot \mathrm{\Delta },\\ S_2=-\frac{(\sqrt{3}-1)\cdot A_1\cdot E}{2\cdot h}\cdot \mathrm{\Delta },\\ S_3=-\frac{(\sqrt{3}-3)\cdot A_1\cdot E}{2\cdot h}\cdot \mathrm{\Delta }\end{array}$.

📑 toggle code

/*******************************************************/
sol[1] : solve([diff(U,u) = 0, diff(U,v) = 0],[u,v])[1];
sol[2] : ratsimp(subst([h-delta=h],subst(sol[1],makelist(S[i] = subst(par,subst(Sigma,A[i]*sigma[i])),i,1,3))));

Post-Processing

Potential U(u,v).

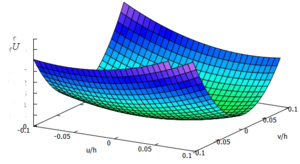
Das Potential können wir über u,v plotten - die Gleichgewichtsbeziehung ist im Minimum der Fläche.

📑 toggle code

/*******************************************************/
/* plots */

Upsilon: ratsimp(subst([gamma = 1/100], subst([u=alpha*h,v=beta*h, delta = gamma*h],U)/(E*A[1]*h)));
plot3d(Upsilon,[alpha,-1/10,1/10],[beta,-1/10,1/10])

Links

• ...

Literature

• ...