Gelöste Aufgaben/FEAC

Aufgabenstellung

Hier berechnen wir die analytische Lösung zur Aufgabe FEAA.

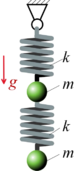
Gesucht ist die analytische Lösung für die statische Auslenkung der beiden Massen. Wir arbeiten dabei mit dem Prinzip vom Minimum der Potentiellen Energie.

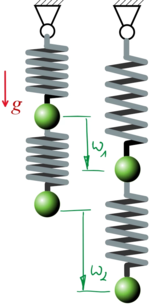
Als Koordinaten führen wir die Auslenkungen der Massen aus Ihrer Referenzlage ein, in der Referenzlage sind die Federn entspannt.

Das Potential für das Aufstellen der Gleichgewichtsbeziehung lautet

U = Π - A

,

wobei

\begin{array}{ll} A & = w_{2} \cdot g \cdot m + w_{1} \cdot g \cdot m, \\ Π & = \frac{{(w_{2} - w_{1})}^{2} \cdot k}{2} + \frac{w_{1}^{2} \cdot k}{2} \end{array}

Die Gleichgewichtsbeziehungen nach dem Prinzips vom Minimum der Potentiellen Energie

\frac{d U}{d w_{i}} \overset{!}{=} 0

.

liefern die Gleichungen

\begin{array}{l} g \cdot m + (w_{2} - w_{1}) \cdot k - w_{1} \cdot k = 0, \\ g \cdot m - (w_{2} - w_{1}) \cdot k = 0 \end{array}

.

bzw. in Matrixform

\underline{\underline{A}} \cdot (\begin{matrix} w_{1} \\ w 2 \end{matrix}) = \underline{b}

mit

\underline{\underline{A}} = k (\begin{matrix} 2 & - 1 \\ - 1 & 1 \end{matrix}), \underline{b} = m \cdot g (\begin{matrix} 1 \\ 1 \end{matrix})

Das Gleichungssystem hat sie Lösung (vgl. Minimum Prinzipe)

[w_{1} = \frac{2 \cdot g \cdot m}{k}, w_{2} = \frac{3 \cdot g \cdot m}{k}]

.

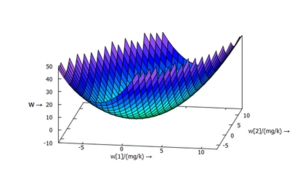
Das dimensionslos-gemachte Potential U ist hier über w₁ und w₂ aufgetragen: man erkennt das Minimum des Potentials bei der berechneten Lösung.

Links

Literature