Gelöste Aufgaben/FEAB
Aufgabenstellung
Statt zwei Freiheitsgraden wie in FEAA haben wir jetzt - bei einem Kontinuum - unendlich viele.
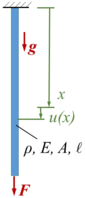
Gesucht ist die Näherungslösung für die Auslenkung der Stab-Querschnitte mit dem Prinzip der Virtuellen Verrückungen. Wir verwenden polynomialen Ansatzfunktionen über die Gesamtlänge - also eine Mischung aus Finiten-Elemente-Methode und dem Rayleigh-Ritz-Verfahren.
Lösung mit Maxima
Header
In den Lageplan haben wir bereits den funktionalen Fireheitsgrad u(x) eingetragen, der Stab ist am oberen Ende befestigt und wird am unteren Ende mit der Zugkraft F belastet.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-10-10 */
/* ref: FENV step 4 im Prozess: Ganzfeldansätze */
/* description: mit dem PvV werden die Bewegungsgl. */
/* für einen Stab unter Gewichtskraft erstellt*/
/*******************************************************/
Declarations
Für Maxima brauchen wir einige Deklarationen.
Der maximale Exponent des Ansatz-Polynoms ist drei - dann nämlich fällt die Näherungslösung mit der analytischen Lösung zusammen.
Hier wählen wir
- (im Maxima-Skipt I=3)
/*******************************************************/
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δQ", alphabetic);
declare("δu", alphabetic);
/*******************************************************/
/* parameter */
I : 3; /* max: 3*/
Formfuctions
Für die Formfunktionen wählen wir
- > ,
also für I=2
und entsprechend
- .
/* coordinates and their variations */
Q : makelist( U[i],i,1,I);
δQ : makelist(δU[i],i,1,I);
/* trial functions */
Phi : [(x/l)^1,(x/l)^2,(x/l)^3];
/* Ansatz */
u : sum( Q[i]*Phi[i],i,1,I);
δu : sum(δQ[i]*Phi[i],i,1,I);
Equilibrium Conditions
Die Gleichgewichtsbedingung
liefert
- .
/* Equilibrium */
δΠ : E*A*integrate(diff(u,x)*diff(δu,x),x,0,l);
δA : integrate(rho*g*A*δu, x,0,l);
Solving
Die Gleichgewichtsbedingungen folgen daraus zu
und somit
eom : makelist(-coeff(expand(δA-δΠ),c)=0,c,δQ);
sol: solve(eom, Q)[1];
Post-Processing
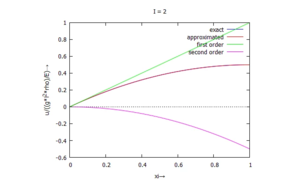
Und wir tragen die Ergebnisse auf für die numerische Näherungslösung
gegen die exakte Lösung auf:
| ✔ Spannungen im Stab: |
| Tragen Sie auch die Spannungen im Stab über die Stablänge an! Berechnen Sie die Spannungen auf Basis der Dehnung
|
/* plot results*/
toPlot: append([xi*(1-xi/2)],
[ expand(subst(xi*l,x,subst(sol,sum(Q[i]*Phi[i],i,1,I)/(rho*g*l^2/E))))],
makelist( subst(xi*l,x,subst(sol, Q[i]*Phi[i] /(rho*g*l^2/E))), i,1,I));
plot2d(toPlot, [xi,0,1], [xlabel, "xi→"], [ylabel, "u/((g*l^2*rho)/E)→"],
[legend, "exact", "approximated", "first order", "second order", "third order"],
[title, sconcat("I = ",I)]);
Links
- ...
Literature
- ...