Gelöste Aufgaben/FEC1/FEC1 - Teil II: Das Modell erstellen

⬅ Zurück zu Teil I

Mathematisches Modell formulieren

Die Bewegungsgleichungen leiten wir mit dem Prinzip der virtuellen Verrückungen her, die Gleichgewichtsbedingung lautet also

${\begin{array}{lcl}\delta W&=&\delta W^{a}-\delta \Pi \\&{\stackrel {!}{=}}&0\end{array}}$.

Die Anteile ergeben sich jeweils aus der Summe der Teilsysteme

$\displaystyle \delta W^{a}=\sum _{i}W_{i}^{a},\;\;\;\delta \Pi =\sum _{i}\Pi _{i}$

mit

$i\in \left\{S,I,T,B_{B},B_{C},U_{A},U_{D}\right\}$ .

Auf keines der Teilsysteme wirkt eine äußere, eingeprägte Last (keine Kraft, kein Moment) - es treten also nur die Anteile der d'Alembert'schen Kräfte und der Formänderungsenergie auf.

Impeller- und Turbinen-Rad sowie die Unwuchten erfassen wir als Starrkörper - ihre virtuelle Formänderungsenergie ist Null:

${\begin{array}{lc}\delta \Pi _{I}&=0\\\delta \Pi _{T}&=0\\\delta \Pi _{U,A}&=0\\\delta \Pi _{U,D}&=0\end{array}}$ .

Für die beiden Lager berücksichtigen wir keine Massen, hier ist also

${\begin{array}{lc}\delta W_{B,B}&=0\\\delta W_{B,C}&=0\end{array}}$ .

Die verbleibenden virtuellen Arbeiten des Systems schreiben wir an, sortieren nach den Koordinaten und deren Variation und formen daraus das System von Bewegungsgleichungen.

tmp

Diskretisierung der Welle

Die Welle ist ein elastisches Kontinuum. Wir können sie als Stab (als eindimensionales Kontinuum) modellieren. Dabei passen

• ein Euler-Bernoulli-Balken oder
• ein Timoshenko-Balken.

Der Einfachheit halber wählen wir den klassischen Euler-Bernoulli-Balken. Die Ansatzfunktionen und Element-Steifigkeits-Matrizen nehmen wir aus der FEM-Formulierung für den Euler-Bernoulli-Balken.

Für die Komplexität des Modells ist die Anzahl der Finiten Elemente entscheidend. Jeder Knoten eines Finite Elements für diesen 3D-Euler-Bernoulli-Ballken hat die vier Koordinaten

${\begin{array}{c}V_{i}(t)\\\Psi _{i}(t)\\W_{i}(t)\\\Phi _{i}(t)\end{array}}$.

Die Anzahl der Koordinaten K ist also mit N als Anzahl der Elemente

$K=4\cdot (N+1)$

Uns geht es hier primär um die Anschaulichkeit - wir approximieren die Bewegung der Welle mit einem Finiten Element.

Damit sind die Koordinaten der Welle - und damit des Gesamt-Systems

Hier steht der Index 0 für Punkt A und Index 1 für Punkt B.

/*******************************************************/
/******************* PART   I **************************/
/*******************************************************/

/* define trial functions */
trial: w(x,t) = sum(a[i]*xi^i,i,0,3);
nodal : [W[0](t)  = subst([xi=0],subst(trial,w(x,t))),
         Φ[0](t)  = subst([xi=0],diff(subst(trial,w(x,t)),xi)/ℓ),
         W[1](t)  = subst([xi=1],subst(trial,w(x,t))),
         Φ[1](t)  = subst([xi=1],diff(subst(trial,w(x,t)),xi)/ℓ)];
trial: ratsimp(subst(solve(nodal,makelist(a[i],i,0,3))[1],trial));
/* translate to y-direction */
trial: [trial, subst([w(x,t)=v(x,t),W[0](t)=V[0](t),W[1](t)=V[1](t), Φ[0](t)=Ψ[0](t), Φ[1](t)=Ψ[1](t)],trial)];

/* shaft nodal coordinates */
Q: [[ V[0](t),  Ψ[0](t),  W[0](t),  Φ[0](t),  V[1](t),  Ψ[1](t),  W[1](t),  Φ[1](t),  V[i](t),  Ψ[i](t),  W[i](t),  Φ[i](t)], 
    [δV[0]   , δΨ[0]   , δW[0]   , δΦ[0]   , δV[1]   , δΨ[1]   , δW[1]   , δΦ[1]   , δV[i]   , δΨ[i]   , δW[i]   , δΦ[i]   ]];
/* variation of coordinates            */
varia: makelist(Q[1][i]=Q[2][i],i,1,8);
/* null-reference for linearization   */
nuller : makelist(Q[1][i]=0,i,1,12);

Virtuelle Arbeit von D'Alembert'schen Trägheitkräften

Allgemein ist die Virtuelle Arbeit von D'Alembert'schen Trägheitkräften definiert als

$\displaystyle \delta W^{a}=\int _{V}(-\rho \;{\ddot {\vec {r}}})\cdot \delta {\vec {r}}\;dV$.

Wir brauchen also nur einen Ortsvektor zu den materiellen Punkten der Körper als Funktion der Koordinaten der Bewegung - den wir dann in die Beziehung oben einsetzen und über das Volumen des Körpers integrieren.

tmp

Virtuelle Arbeit von D'Alembert'schen Trägheitkräften der Welle

Wir beschreiben den Ort "x₁" der neutralen Faser der Welle durch die funktionalen Koordinaten v(x₁,t) und w(x₁,t) im rotierenden Koordinatensystem. In diesem ist

${\begin{array}{ll}{\vec {r}}_{N}(x_{1},t)&=x_{1}\cdot {\vec {e}}_{x,1}+v(x,t)\cdot {\vec {e}}_{y,1}+w(x,t)\cdot {\vec {e}}_{z,1}\\&=(x_{1},v,w)\cdot \left({\begin{array}{c}{\vec {e}}_{x,1}\\{\vec {e}}_{y,1}\\{\vec {e}}_{z,1}\end{array}}\right)\\&=(x_{1},v,w)\cdot {\underline {\vec {e}}}_{1}\end{array}}$

mit den Einheits-Vektoren des rotierenden Koordinatensystems

${\vec {e}}_{x,1}(t),{\vec {e}}_{y,1}(t),{\vec {e}}_{z,1}(t))$.

In Kurzform schrieben wir den Ortsvektor als

${\vec {r}}_{N}={\underline {r}}_{N}\cdot {\underline {\vec {e}}}_{1}$.

mit

${\underline {r}}_{N}^{T}=\left({\begin{array}{c}x_{1}\\v(x_{1},t)\\w(x_{1},t)\end{array}}\right)$ und ${\underline {\vec {e}}}_{1}=\left({\begin{array}{c}{\vec {e}}_{x,1}\\{\vec {e}}_{y,1}\\{\vec {e}}_{z,1}\end{array}}\right)$.

Um vom  

${\begin{array}{ll}{\underline {\vec {e}}}_{0}&\ldots {\text{ Inertialsystem in das}}\\{\underline {\vec {e}}}_{1}&\ldots {\text{ rotierende Koordinatensystem}}\end{array}}$

zu transformieren, arbeiten wir mit der Eulerschen Drehmatrix in der Form

${\underline {\vec {e}}}_{1}={\underline {\underline {D}}}_{1}(\Omega \,t)\cdot {\underline {\vec {e}}}_{0}$

Die Beschleunigung eines Schwerpunkts des Querschnitts "x" erhalten wir dann durch die zweite Ableitung des Ortsvektors nach der Zeit. Das ist nicht ganz trivial, weil wir nun die Ableitung der Einheitsvektoren im rotierenden Koordinatensystem berücksichtigen müssen. Wir starten deshalb mit der ersten Zeitableitung, der Geschwindigkeit. Hier ist - mit der Produktregel -

${\dot {\vec {r}}}_{N}={\dot {\underline {r}}}_{N}\cdot {\underline {\vec {e}}}_{1}+{\underline {r}}_{N}\cdot {\dot {{\underline {\vec {e}}}_{1}}}$

mit

${\dot {{\underline {\vec {e}}}_{1}}}={\dot {\underline {\underline {D}}}}_{1}(\Omega \,t)\cdot {\underline {\vec {e}}}_{0}$.

Ausführlich geschrieben steht dort

${\begin{array}{lc}\displaystyle {\frac {{\vec {r}}_{N}(x_{1},t)}{dt}}:={\dot {\vec {r}}}_{N}(x_{1},t)=&\displaystyle \;\;\underbrace {{\frac {d}{dt}}\left(x_{1}\cdot {\vec {e}}_{x,1}\right)} _{\displaystyle =0}\\&\displaystyle +\underbrace {{\frac {d}{dt}}\left(v(x,t)\cdot {\vec {e}}_{y,1}\right)} _{\displaystyle ={\dot {v}}(x,t)\cdot {\vec {e}}_{y,1}+v(x,t)\cdot {\dot {\vec {e}}}_{y,1}}\\&\displaystyle +\underbrace {{\frac {d}{dt}}\left(w(x,t)\cdot {\vec {e}}_{z,1}\right)} _{\displaystyle ={\dot {w}}(x,t)\cdot {\vec {e}}_{z,1}+w(x,t)\cdot {\dot {\vec {e}}}_{z,1}}\end{array}}$.

Einsetzten liefert für die Einheitsvektoren im gedrehten "1"-System (s.o.)

$\underbrace {\begin{pmatrix}{{\vec {e}}_{x,1}}\\{{\vec {e}}_{y,1}}\\{{\vec {e}}_{z,1}}\end{pmatrix}} _{\displaystyle :={\underline {\vec {e}}}_{1}}={\begin{pmatrix}{{\vec {e}}_{x,0}}\\\cos {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{y,0}}-\sin {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{z,0}}\\\cos {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{z,0}}+\sin {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{y,0}}\end{pmatrix}}$

Und damit ist z.B.

${\dot {\vec {e}}}_{y,1}=-\Omega \cos {\left(\Omega \,t\right)}{{\vec {e}}_{z,0}}-\Omega \sin {\left(\Omega \,t\right)}{{\vec {e}}_{y,0}}$und

${\dot {\vec {\underline {e}}}}_{1}={\begin{pmatrix}0\\-\Omega \,\cos {\left(\Omega \,t\right)}\;{{\vec {e}}_{z,0}}-\Omega \,\sin {\left(\Omega \,t\right)}\;{{\vec {e}}_{y,0}}\\+\Omega \,\cos {\left(\Omega \,t\right)}\;{{\vec {e}}_{y,0}}-\Omega \,\sin {\left(\Omega \,t\right)}\;{{\vec {e}}_{z,0}}\end{pmatrix}}$.

Die zweite Ableitung nach der Zeit liefert analog

${\ddot {\vec {\underline {e}}}}_{1}={\begin{pmatrix}0\\+{{\Omega }^{2}}\sin {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{z,0}}-{{\Omega }^{2}}\cos {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{y,0}}\\-{{\Omega }^{2}}\cos {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{z,0}}-{{\Omega }^{2}}\sin {\left(\Omega \,t\right)}\cdot {{\vec {e}}_{y,0}}\end{pmatrix}}$

Die Variation des Ortsvektors erhalten wir, indem wir im Ausdruck für

${\vec {r}}_{N}$

• die Terme zu Null setzen, die wir nicht variieren dürfen und
• die Koordinaten v(x,t), w(x,t) durch ihre Variation δv(x), δw(x) ersetzen, also
  $\delta {\vec {r}}_{N}(x_{1})=0+\delta v(x)\cdot {\vec {e}}_{y,1}+\delta w(x)\cdot {\vec {e}}_{z,1}$.

Einsetzten in die Formel für die Virtuelle Arbeit von D'Alembert'schen Trägheitkräften liefert zunächst

$-{\ddot {\vec {r}}}_{N}\cdot \delta {\vec {r}}_{N}=-{\ddot {v}}\cdot \delta v-{\ddot {w}}\cdot \delta w-2\Omega \left({\dot {v}}\cdot \delta w-{\dot {w}}\cdot \delta v\right)+\Omega ^{2}\left(v\cdot \delta v+w\cdot \delta w\right)$

Wir setzen nun die Trial-Functions für kubische Ansatz-Polynome für v(x,t), w(x,t) ein, führen die Integration über die Länge ℓ der Welle und den Querschnitt A aus - wobei wir die Trägheitsmomente aus dem Kippen der Querschnitte vernachlässigen - und erhalten

$\delta W_{S}^{a}=\delta {\underline {Q}}^{T}\cdot \left({\underline {\underline {M}}}_{S}\cdot {\underline {\ddot {Q}}}+{\underline {\underline {G}}}_{S}\cdot {\underline {\dot {Q}}}+{\underline {\underline {K}}}_{S}\cdot {\underline {Q}}\right)$

mit

${\underline {\underline {M}}}_{S}=\;\;\;\;m_{S}\;{\begin{pmatrix}{\frac {13}{35}}&{\frac {11\ell }{210}}&0&0&{\frac {9}{70}}&-{\frac {13\ell }{420}}&0&0\\{\frac {11\ell }{210}}&{\frac {{\ell }^{2}}{105}}&0&0&{\frac {13\ell }{420}}&-{\frac {{\ell }^{2}}{140}}&0&0\\0&0&{\frac {13}{35}}&{\frac {11\ell }{210}}&0&0&{\frac {9}{70}}&-{\frac {13\ell }{420}}\\0&0&{\frac {11\ell }{210}}&{\frac {{\ell }^{2}}{105}}&0&0&{\frac {13\ell }{420}}&-{\frac {{\ell }^{2}}{140}}\\{\frac {9}{70}}&{\frac {13\ell }{420}}&0&0&{\frac {13}{35}}&-{\frac {11\ell }{210}}&0&0\\-{\frac {13\ell }{420}}&-{\frac {{\ell }^{2}}{140}}&0&0&-{\frac {11\ell }{210}}&{\frac {{\ell }^{2}}{105}}&0&0\\0&0&{\frac {9}{70}}&{\frac {13\ell }{420}}&0&0&{\frac {13}{35}}&-{\frac {11\ell }{210}}\\0&0&-{\frac {13\ell }{420}}&-{\frac {{\ell }^{2}}{140}}&0&0&-{\frac {11\ell }{210}}&{\frac {{\ell }^{2}}{105}}\end{pmatrix}}$,

${\underline {\underline {G}}}_{S}=\;\;m_{S}\;\Omega \;{\begin{pmatrix}0&0&{\frac {26}{35}}&{\frac {11\ell }{105}}&0&0&{\frac {9}{35}}&-{\frac {13\ell }{210}}\\0&0&{\frac {11\ell }{105}}&{\frac {2{{\ell }^{2}}}{105}}&0&0&{\frac {13\ell }{210}}&-{\frac {{\ell }^{2}}{70}}\\-{\frac {26}{35}}&-{\frac {11\ell }{105}}&0&0&-{\frac {9}{35}}&{\frac {13\ell }{210}}&0&0\\-{\frac {11\ell }{105}}&-{\frac {2{{\ell }^{2}}}{105}}&0&0&-{\frac {13\ell }{210}}&{\frac {{\ell }^{2}}{70}}&0&0\\0&0&{\frac {9}{35}}&{\frac {13\ell }{210}}&0&0&{\frac {26}{35}}&-{\frac {11\ell }{105}}\\0&0&-{\frac {13\ell }{210}}&-{\frac {{\ell }^{2}}{70}}&0&0&-{\frac {11\ell }{105}}&{\frac {2{{\ell }^{2}}}{105}}\\-{\frac {9}{35}}&-{\frac {13\ell }{210}}&0&0&-{\frac {26}{35}}&{\frac {11\ell }{105}}&0&0\\{\frac {13\ell }{210}}&{\frac {{\ell }^{2}}{70}}&0&0&{\frac {11\ell }{105}}&-{\frac {2{{\ell }^{2}}}{105}}&0&0\end{pmatrix}}$,

${\underline {\underline {K}}}_{S}=m_{S}\;\Omega ^{2}\;{\begin{pmatrix}-{\frac {13}{35}}&-{\frac {11\ell }{210}}&0&0&-{\frac {9}{70}}&{\frac {13\ell }{420}}&0&0\\-{\frac {11\ell }{210}}&-{\frac {{\ell }^{2}}{105}}&0&0&-{\frac {13\ell }{420}}&{\frac {{\ell }^{2}}{140}}&0&0\\0&0&-{\frac {13}{35}}&-{\frac {11\ell }{210}}&0&0&-{\frac {9}{70}}&{\frac {13\ell }{420}}\\0&0&-{\frac {11\ell }{210}}&-{\frac {{\ell }^{2}}{105}}&0&0&-{\frac {13\ell }{420}}&{\frac {{\ell }^{2}}{140}}\\-{\frac {9}{70}}&-{\frac {13\ell }{420}}&0&0&-{\frac {13}{35}}&{\frac {11\ell }{210}}&0&0\\{\frac {13\ell }{420}}&{\frac {{\ell }^{2}}{140}}&0&0&{\frac {11\ell }{210}}&-{\frac {{\ell }^{2}}{105}}&0&0\\0&0&-{\frac {9}{70}}&-{\frac {13\ell }{420}}&0&0&-{\frac {13}{35}}&{\frac {11\ell }{210}}\\0&0&{\frac {13\ell }{420}}&{\frac {{\ell }^{2}}{140}}&0&0&{\frac {11\ell }{210}}&-{\frac {{\ell }^{2}}{105}}\end{pmatrix}}$,

und der Wellen-Masse

$m_{S}=\rho \;A\;\ell$.

Im rotierenden Koordinatensystem kommen wir zusätzlich zur gewohnten Massenmatrix M_S nun also die Gyroskopie-Matrix G_S und die Zentrifugal-Matrix K_S.

Hier steht bereits die Grundform der System-Matrizen von oben - es fehlen nur noch die Anteile der starren Teilsysteme Impeller,Turbine und Unwucht.

/*******************************************************/
/******************* PART  II **************************/
/*******************************************************/
/* virtuel work of d'Alembert forces                   */
/*******************************************************/

/***********************************/
/* matrices from d'Alembert forces
                           of shaft*/
 r : expand(subst(trial,matrix([0,v(x,t),w(x,t)]).D[1](Omega*t)));
δr : sum(subst(nuller,diff(r,Q[1][i]))*Q[2][i],i,1,8);
δW[S] :-expand(ℓ*integrate(expand(rho*A*   diff(r,t,2).   δr   ),xi,0,1))$
δW[S] : subst(solve(params[1][3],A),δW[S])$

MS : trigsimp(funmake('matrix,makelist(makelist(coeff(coeff(-δW[S],Q[2][j]),diff(Q[1][k],t,2)),j,1,8),k,1,8)))$
GS : trigsimp(funmake('matrix,makelist(makelist(coeff(coeff(-δW[S],Q[2][j]),diff(Q[1][k],t,1)),j,1,8),k,1,8)))$
KS : trigsimp(funmake('matrix,makelist(makelist(coeff(coeff(-δW[S],Q[2][j]),diff(Q[1][k],t,0)),j,1,8),k,1,8)))$

tmp

Virtuelle Arbeit von D'Alembert'schen von Impeller- und Turbinen-Rad

Impeller-und Turbinen-Rad modellieren wir als Starrkörper.

Eine Verschiebung in Wellen-Längsachse betrachten wir nicht, der Drehwinkel Ω t ist fest gegeben - es bleiben also  für jeden Knoten i = A, D noch die Freiheitsgrade

${\underline {Q}}_{i}=\left({\begin{array}{c}V_{i}(t)\\\Psi _{i}(t)\\W_{i}(t)\\\Phi _{i}(t)\end{array}}\right)$

Die Virtuelle Arbeit von d'Alembert'schen Trägheitskräften des Impeller- oder Turbinen-Rades "i" erhalten wir nun wieder aus dem Integral der Beiträge über alle seine materiellen Punkte. Um zu einem beliebigen Punkt auf dem Rad - hier dem Impeller - zu kommen, brauchen wir zuerst den Ortsvektor zu Punkt A:

${\vec {r}}_{A}(t)=\left(0,V_{A}(t),W_{A}(t)\right).{\underline {\vec {e}}}_{1}$

Koordinaten zu einem materiellen Punkt P auf dem Impeller.

Von Punkt A zu Punkt P kommen wir im Impeller-festen Koordinatensystem

$\Delta {\vec {r}}_{AP}=\left(x_{2},y_{2},z_{2}\right)\cdot {\underline {\vec {e}}}_{2}$ mit ${\underline {\vec {e}}}_{2}={\underline {\underline {D}}}_{3}(\Psi _{i}(t))\cdot {\underline {\underline {D}}}_{2}(-\Phi _{i}(t))\cdot {\underline {\vec {e}}}_{1}$.

Die Integration über den zylindrischen Impeller schaffen wir einfacher in Polarkoordinaten

$\left(x_{2},y_{2},z_{2}\right)=\left(x_{2},{\tilde {y}},0\right)\cdot {\underline {\underline {D}}}_{1}(\zeta )$

Für die Ebene x₂=0 ist das

${\vec {r}}_{P}=(0,V_{A},W_{A})\cdot {\underline {\vec {e}}}_{1}+\left(0,{\tilde {y}},0\right)\cdot {\underline {\underline {D}}}_{1}(\eta )\cdot {\underline {\vec {e}}}_{2}$.

Die beiden Kippungen um die y₁- und z₁-Achse sind klein, es gilt

$\Phi _{A}\ll 1{\text{ und }}\Psi _{A}\ll 1$.

Wir linearisieren deshalb bezüglich dieser Winkel.

Für x₂=0 ist dieser Punkt P noch in der y-z-Ebene von Punkt A. Wir müssten nun die Integration über den komplexen Impeller mit seinen Schaufeln ausführen - mit analytischen Ansätzen hoffnungslos! Wir stellen uns vor, der Impeller sei eine Scheibe mit konstante Dicke "w". Und statt die Integration explizit in x₂-Richtung auszuführen, multiplizieren wir einfach (vereinfachend) mit der Dicke der imaginären Scheibe w.

Wir führen also die Integration über

$dV=w\cdot {\tilde {y}}\;d\zeta \;d{\tilde {y}}$

für

$0<{\tilde {y}}<R{\text{ und }}0<\zeta <2\pi$

aus und erhalten - hier für den Impeller -

$\delta W_{I}^{a}=-\delta {\underline {Q}}_{A}^{T}\cdot \left({\underline {\underline {M}}}_{I}\cdot {\underline {\ddot {Q}}}_{A}+{\underline {\underline {G}}}_{I}\cdot {\underline {\dot {Q}}}_{A}+{\underline {\underline {K}}}_{I}\cdot {\underline {Q}}_{A}\right)$

mit

${\underline {\underline {M}}}_{I}=\;\;\;\;{\begin{pmatrix}{m_{I}}&0&0&0\\0&{J_{I}}&0&0\\0&0&{m_{I}}&0\\0&0&0&{J_{I}}\end{pmatrix}}$,

${\underline {\underline {G}}}_{I}=2\Omega {\begin{pmatrix}0&0&{m_{I}}&0\\0&0&0&-{J_{I}}\\-{m_{I}}&0&0&0\\0&{J_{I}}&0&0\end{pmatrix}}$,

${\underline {\underline {K}}}_{I}=\Omega ^{2}\;{\begin{pmatrix}-{m_{I}}&0&0&0\\0&-{J_{I}}&0&0\\0&0&-{m_{I}}&0\\0&0&0&-{J_{I}}\end{pmatrix}}$.

Die Matrizen des Teilsystems Turbine sind die gleichen - nur mit dem Intex T statt I!

Komposition der Gesamtmatrix

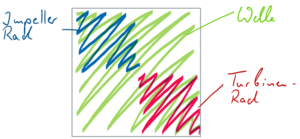
Wir bauen die Matrizen der Teilsysteme wie im Bild links in das Gesamtsystem ein.

Jetzt fehlt noch die Unwucht.

/* displacement of mass point P 
   on either Impeller- or Turbine-Wheel*/
r : expand(matrix([0,V[i](t),W[i](t)]).D[1](Omega*t)
          +matrix([0,   y   ,  0    ]).D[1](zeta).DL[2](-Φ[i](t)).DL[3](Ψ[i](t)).D[1](Omega*t))$
/* linearize*/
r : subst(nuller,r) + sum(subst(nuller,diff(r,Q[1][j]))*Q[1][j],j,9,12)$
/* Variation of ...*/
δr : sum(subst(nuller,diff(r,Q[1][j]))*Q[2][j],j,9,12)$

δW[W] :-expand(integrate(integrate(expand(w*y*rho*  diff(r,t,2). δr  ), zeta,0,2*%pi),y,0,R))$
δW[W] : subst( append(solve(subst(params[1][2],params[1][1]),R^4), solve(params[1][2],R^2)),δW[W]);

/***********************************/
/* matrices from d'Alembert forces
                    of rigid wheels*/
MW : trigsimp(funmake('matrix,makelist(makelist(coeff(coeff(-δW[W],Q[2][j]),diff(Q[1][k],t,2)),j,9,12),k,9,12)))$
GW : trigsimp(funmake('matrix,makelist(makelist(coeff(coeff(-δW[W],Q[2][j]),diff(Q[1][k],t,1)),j,9,12),k,9,12)))$
KW : trigsimp(funmake('matrix,makelist(makelist(coeff(coeff(-δW[W],Q[2][j]),diff(Q[1][k],t,0)),j,9,12),k,9,12)))$

tmp

Virtuelle Arbeit von D'Alembert'schen der Unwucht

Eine Unwucht hat die Gesamtmasse m_U. Wir setzen m_U ≪ m_i' und m_U ≪ m_T' an, dann brauchen wir unten die Anteile der Unwucht in den System-Matrizen M, G und K nicht berücksichtigen. Was bleibt dann?.

Der Ortsvektor zur "vorderen" (positive x-Koordinate) der Hantelmassen ist

${\begin{array}{ll}{\vec {r}}_{U,1}(t)=&\,\;\;\;\left(0,V_{A},W_{A}\right)\cdot {\underline {\vec {e}}}_{1}\\&\displaystyle +\left(0,0,e\right)\cdot {\underline {\vec {e}}}_{2}\\&\displaystyle +\left(+a,0,0\right)\cdot {\underline {\underline {D}}}_{2}(\varphi )\cdot {\underline {\vec {e}}}_{2}\end{array}}$

Die Virtuelle Arbeit von D'Alembert'schen Trägheitskräften für diese Hälfte der Hantel-Masse erhalten wir aus

$\displaystyle \delta W_{U,1}=\left(-{\frac {m_{U}}{2}}\;{\ddot {\vec {r}}}_{U,1}\right)\cdot \delta {\vec {r}}_{U,1}$

Den Term für die zweite Masse der Hantel (Index "U,2") erhalten wir, wenn wir die Länge "a" durch "-a" ersetzen. Dann ist

${\begin{array}{ll}\delta W_{U}&=\delta W_{U,1}+\delta W_{U,2}\end{array}}$

Wir erhalten in Matrix-Schreibweise - hier für die Unwucht am Impeller (bei A) -

$\delta W_{U,A}^{a}=-\delta {\underline {Q}}_{A}^{T}\cdot \left({\underline {\underline {M}}}_{U}\cdot {\underline {\ddot {Q}}}_{A}+{\underline {\underline {G}}}_{U}\cdot {\underline {\dot {Q}}}_{A}+{\underline {\underline {K}}}_{U}\cdot {\underline {Q}}_{A}-{\underline {P}}_{U}\right)$

mit

${\underline {\underline {M}}}_{U}=\;\;\;\;m_{U}\,{\begin{pmatrix}1&0&0&0\\0&{{a}^{2}}\,{{\cos {(\varphi )}}^{2}}&0&0\\0&0&1&0\\0&0&0&{{e}^{2}}+{{a}^{2}}\end{pmatrix}}$,

${\underline {\underline {G}}}_{U}=2\Omega \,m_{U}\;{\begin{pmatrix}0&0&1&0\\0&0&0&{{a}^{2}}\,{{\cos {(\varphi )}}^{2}}\\-1&0&0&0\\0&-{{a}^{2}}\,{{\cos {(\varphi )}}^{2}}&0&0\end{pmatrix}}$,

${\underline {\underline {K}}}_{U}=\Omega ^{2}\,m_{U}\;{\begin{pmatrix}-1&0&0&0\\0&-{{a}^{2}}\,{{\cos {(\varphi )}}^{2}}&0&0\\0&0&-1&0\\0&0&0&-{{a}^{2}}\,{{\cos {(\varphi )}}^{2}}\end{pmatrix}}$

und

${\underline {P}}_{A}=\Omega ^{2}\,m_{U}\;{\begin{pmatrix}0\\0\\e\\\displaystyle {\frac {{{a}^{2}}\sin {\left(2\varphi \right)}}{2}}\end{pmatrix}}$.

Damit es übersichtlich bleibt, vernachlässigen wir - wegen m_U ≪ m_i' - die Matrizen M_U, G_U und K_U beim Zusammenbau der Gesamt-Gleichungssystems.

Es bleibt: P_A als "rechte Seite" im Gleichungssystem.

/***********************************/
/* matrices from d'Alembert forces
                       of unbalance*/

r : expand(matrix([ 0,  V[i](t),W[i](t)]).D[1](Omega*t)
          +matrix([ 0,    0    ,    e  ]).DL[2](-Φ[i](t)).DL[3](Ψ[i](t)).D[1](Omega*t)
          +matrix([+a,    0    ,    0  ]).D[2](-phi).DL[2](-Φ[i](t)).DL[3](Ψ[i](t)).D[1](Omega*t))$
/* linearize*/
r : subst(nuller,r) + sum(subst(nuller,diff(r,Q[1][j]))*Q[1][j],j,9,12)$
/* Variation of ...*/
δr : sum(subst(nuller,diff(r,Q[1][j]))*Q[2][j],j,9,12)$

δW[U] :-m[U]/2*diff(r,t,2). δr$
δW[U] : expand(subst(nuller,δW[U]))$
/* add second Mass */
δW[U] : expand(trigsimp(δW[U] +subst([a=-a],δW[U])))$
δW[U] : subst([cos(phi)=sin(2*phi)/sin(phi)/2],δW[U]);

/***********************************/
/* right-hand-side from d'Alembert forces
                              of unbalance*/
PU : trigsimp(funmake('matrix,makelist([coeff(+δW[U],Q[2][j])],j,9,12)));

Virtuelle Formänderungsenergie

Zwei elastische Elemente hat unser Modell:

• die Welle und
• die elastischen Lager.

tmp

Virtuelle Formänderungsenergie der Welle

Die Virtuelle Formänderungsenergie für die elastische Welle können wir aus der FEM-Formulierung für den Euler-Bernoulli-Balken kopieren:

$\delta \Pi _{S}=\delta {\underline {Q}}^{T}\cdot {\underline {\underline {K}}}_{S}\cdot {\underline {Q}}$

mit

$\displaystyle {\underline {\underline {K}}}_{S}={\frac {EI}{\ell ^{3}}}{\begin{pmatrix}12&6\ell &0&0&-12&6\ell &0&0\\6\ell &4{{\ell }^{2}}&0&0&-6\ell &2{{\ell }^{2}}&0&0\\0&0&12&6\ell &0&0&-12&6\ell \\0&0&6\ell &4{{\ell }^{2}}&0&0&-6\ell &2{{\ell }^{2}}\\-12&-6\ell &0&0&12&-6\ell &0&0\\6\ell &2{{\ell }^{2}}&0&0&-6\ell &4{{\ell }^{2}}&0&0\\0&0&-12&-6\ell &0&0&12&-6\ell \\0&0&6\ell &2{{\ell }^{2}}&0&0&-6\ell &4{{\ell }^{2}}\end{pmatrix}}$

/*******************************************************/
/* virtuel strain energies                             */
/*******************************************************/
/* matrices from elastic deformation
                          of shaft */
δΠ[S] : integrate(EI*diff(subst(trial,w(x,t)),xi,2)*diff(subst(varia,subst(trial,w(x,t))),xi,2),xi,0,1)/ℓ^3+
        integrate(EI*diff(subst(trial,v(x,t)),xi,2)*diff(subst(varia,subst(trial,v(x,t))),xi,2),xi,0,1)/ℓ^3$
δΠ[S] : expand(subst(solve(params[1][4],EI) ,δΠ[S]))$

KS : funmake('matrix,makelist(makelist(coeff(coeff(δΠ[S],Q[2][i]),diff(Q[1][j],t,0)),i,1,8),j,1,8))$

tmp

Virtuelle Formänderungsenergie der elastischen Lager

Etwas komplizierter wir es bei der virtuellen Formänderungsenergie der Lager.

Auslenkung des Lagers - hier "B".

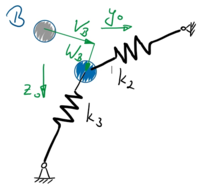
Die Verschiebungen der Welle - hier V_B und W_B für Lager B - haben wir im mitrotierenden Koordinatensystem angegeben. Wenn hier das Turbolader-Gehäuse unterschiedliche Nachgiebigkeiten in y₀ und z₀-Richtung hat, müssen wir die Auslenkungen auf das Intertialsystem transformieren.

Dafür brauchen wir

${\vec {r}}_{B}=\left(\ell _{1},V_{B}(t),W_{B}(t)\right)\cdot {\underline {\vec {e}}}_{1}$

und

$\delta {\vec {r}}_{B}=\left(0,\delta V_{B}(t),\delta W_{B}(t)\right)\cdot {\underline {\vec {e}}}_{1}$

Die virtuelle Formänderungsenergie der beiden Federn ist dann

${\begin{array}{ll}\delta \Pi _{B,B}=&\,\;\;k_{2}\;r_{B,2}\cdot \delta r_{B,2}\\&+k_{3}\;r_{B,3}\cdot \delta r_{B,3}\end{array}}$.

🧨 Gleitlager sind komplizierter:

In Gleitlagern ist die Auslenkung in eine Richtung (z.B. y1) durch die Drehung der Welle immer mit einer Kraft senkrecht zur Auslenkung (z.B. in z1-Richtung) gekoppelt. Das vernachlässigen wir hier.

Einsetzen und Vereinfachen liefert

$\displaystyle \delta \Pi _{B,B}={\frac {1}{2}}\left(\delta V_{B},\delta W_{B}\right)\cdot \left({\begin{array}{c}\left({k_{3}}-{k_{2}}\right){W_{B}}(t)\sin {\left(2\Omega t\right)}+\left({k_{2}}-{k_{3}}\right){V_{B}}(t)\cos {\left(2\Omega t\right)}+\left({k_{3}}+{k_{2}}\right){V_{B}}(t)\\\left({k_{3}}-{k_{2}}\right){V_{B}}(t)\sin {\left(2\Omega t\right)}+\left({k_{3}}-{k_{2}}\right){W_{B}}(t)\cos {\left(2\Omega t\right)}+\left({k_{3}}+{k_{2}}\right){W_{B}}(t)\end{array}}\right)$.

Hier stehen jetzt Terme mit sin(2 Ω t), cos(2 Ω t), die sich auch nicht herauskürzen lassen. Sie führen in der Bewegungsgleichung zu einer Steifigskeits-Matrix (die Koeffizienten), die nicht mehr konstant ist. Diese periodischen Anteile haben alle den Koeffizienten k₃-k₂ - wir führen deshalb

$\Delta k=k_{3}-k_{2}$

ein und schreiben damit die Steifigkeitsmatrizen

${\underline {\underline {K}}}_{B}={\underline {\underline {K}}}_{B,0}+\Delta k\cdot \cos(2\,\Omega \,t)\cdot {\underline {\underline {K}}}_{B,C}+\Delta k\cdot \sin(2\,\Omega \,t)\cdot {\underline {\underline {K}}}_{B,S}$

an. Aber dafür müssen wir zuerst noch die Auslenkungen V_B und W_B in unsere FE-Knoten umrechnen. Wir wählen

$\displaystyle {\frac {\ell _{1}}{\ell _{0}}}={\frac {1}{3}}{\text{ und }}{\frac {\ell _{2}}{\ell _{0}}}={\frac {2}{3}}$

und erhalten z.B. für

$\displaystyle V_{B}(t)={\frac {1}{27}}\;\left(20\;{V_{0}}(t)+7\;V_{1}(t)+4\;\Psi _{0}(t)\ell -2\;\Psi _{1}(t)\ell \right)$.

Damit berechnen wir die Element-Steifigkeits-Matrizen zu

${\underline {\underline {K}}}_{B,0}={\begin{pmatrix}{\frac {449{\mathit {\Delta k}}}{1458}}+{\frac {449{k_{2}}}{729}}&{\frac {47{\mathit {\Delta k}}\ell }{729}}+{\frac {94{k_{2}}\ell }{729}}&0&0&{\frac {140{\mathit {\Delta k}}}{729}}+{\frac {280{k_{2}}}{729}}&-{\frac {34{\mathit {\Delta k}}\ell }{729}}-{\frac {68{k_{2}}\ell }{729}}&0&0\\{\frac {47{\mathit {\Delta k}}\ell }{729}}+{\frac {94{k_{2}}\ell }{729}}&{\frac {10{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}+{\frac {20{k_{2}}\,{{\ell }^{2}}}{729}}&0&0&{\frac {34{\mathit {\Delta k}}\ell }{729}}+{\frac {68{k_{2}}\ell }{729}}&-{\frac {8{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}-{\frac {16{k_{2}}\,{{\ell }^{2}}}{729}}&0&0\\0&0&{\frac {449{\mathit {\Delta k}}}{1458}}+{\frac {449{k_{2}}}{729}}&{\frac {47{\mathit {\Delta k}}\ell }{729}}+{\frac {94{k_{2}}\ell }{729}}&0&0&{\frac {140{\mathit {\Delta k}}}{729}}+{\frac {280{k_{2}}}{729}}&-{\frac {34{\mathit {\Delta k}}\ell }{729}}-{\frac {68{k_{2}}\ell }{729}}\\0&0&{\frac {47{\mathit {\Delta k}}\ell }{729}}+{\frac {94{k_{2}}\ell }{729}}&{\frac {10{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}+{\frac {20{k_{2}}\,{{\ell }^{2}}}{729}}&0&0&{\frac {34{\mathit {\Delta k}}\ell }{729}}+{\frac {68{k_{2}}\ell }{729}}&-{\frac {8{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}-{\frac {16{k_{2}}\,{{\ell }^{2}}}{729}}\\{\frac {140{\mathit {\Delta k}}}{729}}+{\frac {280{k_{2}}}{729}}&{\frac {34{\mathit {\Delta k}}\ell }{729}}+{\frac {68{k_{2}}\ell }{729}}&0&0&{\frac {449{\mathit {\Delta k}}}{1458}}+{\frac {449{k_{2}}}{729}}&-{\frac {47{\mathit {\Delta k}}\ell }{729}}-{\frac {94{k_{2}}\ell }{729}}&0&0\\-{\frac {34{\mathit {\Delta k}}\ell }{729}}-{\frac {68{k_{2}}\ell }{729}}&-{\frac {8{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}-{\frac {16{k_{2}}\,{{\ell }^{2}}}{729}}&0&0&-{\frac {47{\mathit {\Delta k}}\ell }{729}}-{\frac {94{k_{2}}\ell }{729}}&{\frac {10{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}+{\frac {20{k_{2}}\,{{\ell }^{2}}}{729}}&0&0\\0&0&{\frac {140{\mathit {\Delta k}}}{729}}+{\frac {280{k_{2}}}{729}}&{\frac {34{\mathit {\Delta k}}\ell }{729}}+{\frac {68{k_{2}}\ell }{729}}&0&0&{\frac {449{\mathit {\Delta k}}}{1458}}+{\frac {449{k_{2}}}{729}}&-{\frac {47{\mathit {\Delta k}}\ell }{729}}-{\frac {94{k_{2}}\ell }{729}}\\0&0&-{\frac {34{\mathit {\Delta k}}\ell }{729}}-{\frac {68{k_{2}}\ell }{729}}&-{\frac {8{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}-{\frac {16{k_{2}}\,{{\ell }^{2}}}{729}}&0&0&-{\frac {47{\mathit {\Delta k}}\ell }{729}}-{\frac {94{k_{2}}\ell }{729}}&{\frac {10{\mathit {\Delta k}}\,{{\ell }^{2}}}{729}}+{\frac {20{k_{2}}\,{{\ell }^{2}}}{729}}\end{pmatrix}}$,

${\underline {\underline {K}}}_{B,C}={\begin{pmatrix}-{\frac {449}{1458}}&-{\frac {47\ell }{729}}&0&0&-{\frac {140}{729}}&{\frac {34\ell }{729}}&0&0\\-{\frac {47\ell }{729}}&-{\frac {10{{\ell }^{2}}}{729}}&0&0&-{\frac {34\ell }{729}}&{\frac {8{{\ell }^{2}}}{729}}&0&0\\0&0&{\frac {449}{1458}}&{\frac {47\ell }{729}}&0&0&{\frac {140}{729}}&-{\frac {34\ell }{729}}\\0&0&{\frac {47\ell }{729}}&{\frac {10{{\ell }^{2}}}{729}}&0&0&{\frac {34\ell }{729}}&-{\frac {8{{\ell }^{2}}}{729}}\\-{\frac {140}{729}}&-{\frac {34\ell }{729}}&0&0&-{\frac {449}{1458}}&{\frac {47\ell }{729}}&0&0\\{\frac {34\ell }{729}}&{\frac {8{{\ell }^{2}}}{729}}&0&0&{\frac {47\ell }{729}}&-{\frac {10{{\ell }^{2}}}{729}}&0&0\\0&0&{\frac {140}{729}}&{\frac {34\ell }{729}}&0&0&{\frac {449}{1458}}&-{\frac {47\ell }{729}}\\0&0&-{\frac {34\ell }{729}}&-{\frac {8{{\ell }^{2}}}{729}}&0&0&-{\frac {47\ell }{729}}&{\frac {10{{\ell }^{2}}}{729}}\end{pmatrix}}$

und

${\underline {\underline {K}}}_{B,S}={\begin{pmatrix}0&0&{\frac {449}{1458}}&{\frac {47\ell }{729}}&0&0&{\frac {140}{729}}&-{\frac {34\ell }{729}}\\0&0&{\frac {47\ell }{729}}&{\frac {10{{\ell }^{2}}}{729}}&0&0&{\frac {34\ell }{729}}&-{\frac {8{{\ell }^{2}}}{729}}\\{\frac {449}{1458}}&{\frac {47\ell }{729}}&0&0&{\frac {140}{729}}&-{\frac {34\ell }{729}}&0&0\\{\frac {47\ell }{729}}&{\frac {10{{\ell }^{2}}}{729}}&0&0&{\frac {34\ell }{729}}&-{\frac {8{{\ell }^{2}}}{729}}&0&0\\0&0&{\frac {140}{729}}&{\frac {34\ell }{729}}&0&0&{\frac {449}{1458}}&-{\frac {47\ell }{729}}\\0&0&-{\frac {34\ell }{729}}&-{\frac {8{{\ell }^{2}}}{729}}&0&0&-{\frac {47\ell }{729}}&{\frac {10{{\ell }^{2}}}{729}}\\{\frac {140}{729}}&{\frac {34\ell }{729}}&0&0&{\frac {449}{1458}}&-{\frac {47\ell }{729}}&0&0\\-{\frac {34\ell }{729}}&-{\frac {8{{\ell }^{2}}}{729}}&0&0&-{\frac {47\ell }{729}}&{\frac {10{{\ell }^{2}}}{729}}&0&0\end{pmatrix}}$.

/***********************************/
/* matrices from elastic deformation
                        of bearing */
 r : expand(subst(trial,matrix([0,v(x,t),w(x,t)]).D[1](Omega*t)));
δr : sum(subst(nuller,diff(r,Q[1][j]))*Q[2][j],j,1,8);

δΠ[B] : k[2]*r[1][2]*subst(varia,r[1][2])+
        k[3]*r[1][3]*subst(varia,r[1][3])$
δΠ[B] : expand(sum(subst(params[2][i],δΠ[B]),i,1,2))$
δΠ[B] : expand(subst([k[3]=k[2]+Δk],δΠ[B]))$

KB[N] : funmake('matrix,makelist(makelist(trigsimp(coeff(coeff(δΠ[B],Q[2][i]),diff(Q[1][j],t,0))),i,1,8),j,1,8))$
KB[N] : expand(subst(trigReplace[3],expand(subst(trigReplace[2],expand(subst(trigReplace[1],KB[N]))))))$

KB[C] : coeff(KB[N],cos(2*Omega*t))/Δk$
KB[S] : coeff(KB[N],sin(2*Omega*t))/Δk$
KB[N] : KB[N] - Δk*KB[S]*sin(2*Omega*t) - Δk*KB[C]*cos(2*Omega*t)$

/* -> see Matthieus DGL, Ottl 3.11*/

tmp

Komponieren der System-Matrizen

{{{text}}}

1+1

Mathematisches Modell anpassen

Hinschreiben in dimensionsloser Form

{{{text}}}

1+1

Links

• ...

Literature

• ...