Gelöste Aufgaben/FEC1/FEC1 - Teil I: System Strukturieren
Aufgabenstellung
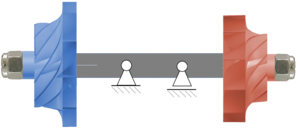
Bei einem Abgas-Turbolader treten Probleme im Betrieb auf, bei denen die Schaufeln entweder des Impellers oder der Turbine zerstört werden.
Untersuchen Sie die Bereiche dynamischer Stabilität eines Turboladers anhand eines linearisierten Modells.
Gegeben:
- Gesamtlänge: 120 mm, Gesamt-Gewicht: 1000 g
- Drehzahl: bis zu 220.000 U/min

Quelle: Quentin Schwinn (NASA) [Public domain], via Wikimedia Commons.
Die Bauteile eines Turboladers zeigt dieses Schnittbild.
- links die Turbinenseite (Impeller, Abgas des Motors),
- rechts der Verdichter (Turbine, für Ansaugluft des Motors).
TEIL I: Declarations Quelle erweitern
Wir untersuchen die Welle mit Impeller und Turbine auf dynamische Instabilität des linearisierten Modells.
Aufgabe präzisieren
Der Turbolader besteht aus
- Gehäuse,
- Turbolader-Welle,
- dem Schmieröl-Kreislauf für die Lager und
- den Strömungen aus Abgas- und Ansaugluft des Motors
Welche Teile müssen wir betrachten - welche können wir weglassen? Das weiß man - wissen wir hier - nicht.
Wenn das System zu einfach ist, eliminieren wir den verantwortlichen Mechanismus, den wir suchen.
Wenn das System zu kompliziert ist, wird es zu teuer (Geld, Ressourcen, Zeit).
Es gibt nur einen Weg: vom Einfachen zum Komplexen. Wir beginnen mit (und hören in diesem Beispiel auch auf mit) dem Bauteil, das wir in jedem Fall modellieren müssen: der Turbolader-Welle.
Sie besteht aus
- Welle
- Impeller- und Turbinen-Rad sowie den
- Lagern.
Wir treffen weitere Entscheidungen:
- Unser Modell soll nur die Strukturmechanik erfassen - die Interaktion mit der Abgas- und Ansaugluft des Motors berücksichtigen wir nicht.
- Wir untersuchen die elastische Welle mit
- aufgesetztem starrem Impeller- und Pumpenrad.
- Bewegungen in Richtung der Turbolader-Welle betrachten wir nicht.
- Eine elastische Verdrillung der Welle betrachten wir nicht.
- Dämpfung berücksichtigen wir nicht.
- Die Lager - meist Gleichlager (SFD, squeeze film dampers) oder FRBs (floating ring bearing) - modellieren wir sehr rudimentär (keine Dämpfung, Rückstellkräfte nur in Auslenkungsrichtung).
Die Bewegungsgleichungen des Systems stellen wir mit dem Prinzip der virtuellen Verrückungen auf. Aus der Literatur zur Dynamik von rotierenden Systemen erwarten wir als Bewegungsgleichung ein System, das so aussieht:
mit
- .
Solche Systeme können aus drei Gründen dynamisch instabil werden:
- die Erregung durch Unwuchten führt zu sehr großen Amplituden des Systems;
- die Anteile der Gyroskopischen Matrix (mit ihren negativen Einträgen) führen zu Instabilität oder
- die periodischen Koeffizienten des Systemes führen zu Instabilität (vgl. Kw30);
System strukturieren
Header
Wir strukturieren unser System "Turboladerwelle", indem wir es gedanklich weiter in Teilsysteme unterteilen:
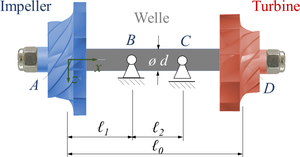
| # | ID | Teilsystem |
|---|---|---|
| 1 | S | Shaft (Welle) |
| 2 | I | Impeller-Rad |
| 3 | T | Turbinen-Rad |
| 4 | Bi | Bearing "i" (Lager); i = B, C |
| 5 | Ui | Unbalance "i" (Unwucht) |

Die ausgezeichneten Punkte auf der Turbolader-Welle sind
A: Schwerpunkt des Impeller-Rades,
B: Lager-Mittelpunkt des linken Lagers,
C: Lager-Mittelpunkt des rechten Lagers,
D: Schwerpunkt des Turbinen-Rades.
Für jedes Teilsystem führen wir nun Koordinaten ein.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 18.10.1 */
/* author: Andreas Baumgart */
/* last updated: 2018-12-29 */
/* ref: Turbo-Charger dynamic instability */
/* description: derives the equations of motion for */
/* a rotating shaft and rigid wheels */
/*******************************************************/
load (lapack)$ /* use lapack for numerics */
fpprintprec : 3$ /* and choose low number of printed dig*/
/*******************************************************/
/* declare additional greek variables */
declare("δW", alphabetic); /* virtual displacement / work */
declare("δV", alphabetic); /* virtual displacement */
declare( "Φ", alphabetic, "δΦ", alphabetic); /* rotation / virtual rotation */
declare( "Ψ", alphabetic, "δΨ", alphabetic); /* rotation / virtual rotation */
declare( "ℓ", alphabetic); /* lengths */
declare("δΠ", alphabetic); /* virtual strain energy */
declare("Δk", alphabetic); /* k[3]-k[2] */
declare("δr", alphabetic); /* virtual displacement vector (column matrix) */
/* indices used:
t ... total
I ... compressor
T ... turbo
S ... shaft
B ... bearing
U ... unbalance
*/
/* Euler - Rotations */
D[1](phi) := matrix([1,0,0],[0,cos(phi),+sin(phi)],[0,-sin(phi),cos(phi)]);
D[2](phi) := matrix([cos(phi),0,-sin(phi)],[0,1,0],[+sin(phi),0,cos(phi)]);
D[3](phi) := matrix([cos(phi),+sin(phi),0],[-sin(phi),cos(phi),0],[0,0,1]);
/* ... linearized */
DL[2](phi) := matrix([1,0,-phi],[0,1,0],[+phi,0,1]);
DL[3](phi) := matrix([1,phi,0],[-phi,1,0],[0,0,1]);
/* trigonometric replacements */
trigReplace : [sin(Omega*t)^2=1-cos(Omega*t)^2, cos(Omega*t)^2=(cos(2*Omega*t)+1)/2, cos(Omega*t)=sin(2*Omega*t)/sin(Omega*t)/2];
/* parameters .... */
params: [[J[i] = m[i]*R^2/4,m[i] = %pi*R^2*w*rho, m[S] = rho*A*ℓ, k[4]=3*EI/ℓ^3],
/* bearing locations */
[xi = 1/3, xi=2/3],
/* reference time */
[omega[0,0]=2*%pi/T]];
Referenz-Zustand
Dabei brauchen wir unabhängige Koordinaten - also materielle Koordinaten der Struktur - und abhängige Koordinaten -also (zeitabhängige) Koordinaten, die die Bewegung des Systems beschrieben.
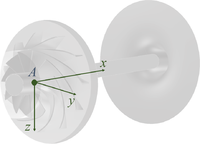
Wir beginnen mit einer Skizze der Turbolader-Welle im Referenz-Zustand: das heißt: keine Verschiebung, keine Verdrehung, keine Verformung.
Den Ursprung unseres Koordinaten-Systems legen wir in Punkt A, die x-Achse durch die Schwerpunkte der Wellen-Querschnittsflächen. y- und z-Achse legen wir senkrecht dazu in jeweils horizontale und vertikale Richtung.
Von dieser Referenzlage aus beschrieben wir die Bewegung des Systems sowohl verbal als auch über abhängige Koordinaten, die wir im folgenden einführen.
Dabei gehen wir gedanklich eine chronologische Abfolge von Bewegungen durch, die das Referenzsystem in das verformte System überführt.
Drehung der Welle
Unsere Turbolader-Welle dreht sich. Durch die Drehung wird unser materielles Koordinatensystem aus dem ursprünglichen Koordinatensystem "herausgedreht".
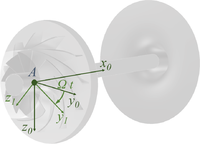
Wir nennen das ursprüngliche, nicht mitgedrehte Koordinatensystem "Inertialsystem" und kennzeichnen es durch den Index "0".
Das zweite, mit der Welle rotierende Koordinatensystem kennzeichnen wir durch den Index "1".
Die Bewegung eines materiellen Punktes (x0,y0,z0) können wir nun also durch Transformationen mit sin- und cos-Funktionen auf ihre Position in der Referenzlage im Inertialsystem "zurückrechnen". Und damit auch deren Beschleunigung berechnen und die D'Alembert'sche Trägheitskraft anschreiben.
So ist z.B.
- .
Zur Vereinfachung gehen wir davon aus, dass die Drehgeschwindigkeit konstant Ω ist, der Drehwinkel also Ω t.
Für unser System brauchen wir einen Ansatz, der diese Transformation - und weitere - formalisiert (→ Drehmatrix).
Auslenkung des Wellen-Querschnitts
Jeder Querschnitt der elastischen Welle mit der materiellen Koordinate x1 (= x0) erfährt eine Auslenkung in die y1- und z1-Richtung von jeweils v(x0,t) und w(x0,t).
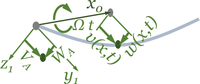
Die Verschiebungen schreiben wir im materiellen (mitdrehenden) Koordinatensystem an - dann können wir mit den Standard-Ausdrücken für die Virtuelle Formänderungsenergie für einen Stab arbeiten. Die ist nämlich unabhängig davon, ob der Stab sich dreht - oder nicht.
Entlang der Welle sind A, B, C und D ausgezeichnete Punkte, hier definieren wir für die Verschiebungen in z1-Richtung:
Analog machen wir das für v(x1,t) in y1-Richtung.
Starrkörper-Bewegung von Impeller- und Turbinen-Rad
Der Impeller-Schwerpunkt erfährt eine Translation in y1- und z1-Richtung (die Verschiebung in x-Richtung haben wir ausgeschlossen) sowie eine Drehungen um die x1-, y1- und z1-Achse.
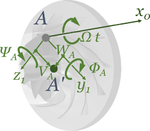
Wir brauchen also vier (abhängige) Koordinaten und den vorgegebene Drehwinkel, um die Bewegung des Pumpenrades eindeutig zu beschrieben.
Der Punkt A der Welle ist mit der Nabe des Impellers fest verbunden - die Verschiebung des Impeller-Schwerpunktes ist also
- .
Die Verdrehung des Impeller-Rades ist
- ,
der Drehwinkel wird mit der Zeit immer größer.
Die Verdrehungen um die y1- und z1-Achse dagegen sind sehr klein - es sind die Kippungen
- .
Damit wir einen konsistenten Anschluss an die Ansatzfunktionen der Finite Elemente Methode schaffen, wählen wir hier
und das bedeutet: die Kippung um die y1-Achse ist positiv definiert entgegen der Konvention für eine positive Drehung!
Für das Turbinen-Rad gelten die gleichen Konventionen, wir tauschen also bei den Indices nur das "A" gegen ein "D".
Starrkörper-Bewegung der Unwuchten
Unwuchten resultieren aus Masseverteilungen, bei denen der Gesamt-Schwerpunkt des Systems nicht wie beabsichtigt in Punkt A auf der x1-Achse liegt oder die Deviationsmomente, z.B.
nicht verschwinden, also
- .
Diese Unwucht können wir in unser System "künstlich" einbauen, im Impeller, indem wir in Punkt A eine gedachte starre "Hantel" mit einer Exzentrizität e unter einem Winkel φ einbauen.
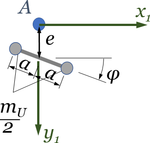
Wir haben
- für e ≠ 0, φ = 0 eine reine statische Unwucht,
- für e = 0, φ ≠ 0 eine reine dynamische Unwucht
eingebaut.
Diese Unwucht hat die gleichen Bewegungs-Koordinaten wie das Impeller-Rad - wir denken uns Hantel und Rad fest verbunden.
Wir werden sehen, dass die Unwucht bei der Berechnung der Instabilität keine wesentliche Rolle spielt - aber wir könnten diese Unwucht natürlich auch in der Turbine einbauen.
Die Verschiebung und Verdrehung jedes Teils der Turbolader-Welle haben wir damit eindeutig festgelegt - jetzt können wir daran gehen, die Gleichgewichtsbedingungen - das mathematische Modell - anzuschreiben.