Gelöste Aufgaben/FEB1
Aufgabenstellung
Auch wenn es nicht so aussieht: für das rotierende Rotorblatt suchen wir eine statische Lösung - das Problem heißt "quasistatisch".
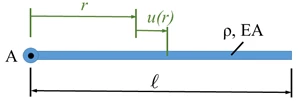
Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte.
Lösung mit Maxima
Declarations
Für die Komposition der Bewegungsgleichungen brauchen wir die Element-Steifigkeitsmatrix und die Element-Lastmatrix.
Wir gehen von gleichlangen Elementen aus, hier von
Elementen, also
- .
Wie im Abschnitt "Finite Elemente Methode" verwenden wir die linearen Ansatzfunktionen
- ,
also
- .
Die Element-Steifigkeitsmatrix ergibt sich für den Dehnstab zu
- .
Die Element-Lastmatrix ist etwas schwieriger. Für ein einzelnes Element i ist
- .
Mit
schreiben die Beziehung um zu
- ,
wir erhalten
- .
/*******************************************************/
/* start: FEM solution */
/* Trial-Fucntions */
phi : [(1-xi), xi];
/* declare System Matrices */
K[i] : funmake('matrix, E*A*l[i]*
makelist(
makelist(
integrate(diff(phi[j],xi)/l[i] *
diff(phi[k],xi)/l[i], xi,0,1),
j,1,2),k,1,2));
P[i] : funmake('matrix, rho*A*Omega^2*l[i]^2*
makelist(
integrate([(n+xi)*phi[j]], xi,0,1),
j,1,2));
/* number of elements */
I : 4;
Equlibrium Conditions
Die Gleichgewichtsbeziehungen des Gesamtsystems erhalten wir durch aus der Addition aller virtuellen Arbeiten des Systems, praktisch durch das Hinzuaddieren der Anteile je Element in die System-Matrizen für K und P:
und
/* initiate system matrices */
K[0] : zeromatrix(I+1,I+1);
P[0] : zeromatrix(I+1, 1 );
/* compose system matrices */
for e : 1 thru I do
for row : 1 thru 2 do
(P[0][e-1+row][ 1 ] : P[0][e-1+row][ 1 ]+subst([n=e-1],P[i][row][ 1 ]),
for col : 1 thru 2 do
K[0][e-1+row][e-1+col] : K[0][e-1+row][e-1+col]+ K[i][row][col]);
Boundary Conditions
Die geometrische Randbedingung U0 = 0 arbeiten wir ein, indem wir die erste Zeile des Gleichungssystem streichen sowie die erste Spalte der Steifigketsmatrix.
/* incorporate geometric boundary conditions */
K[0] : submatrix( 1, K[0], 1);
P[0] : submatrix( 1, P[0] );
Solving
Die Lösung des linearen Gleichungssystems
ist
- .
Oder - in dimensionsloser Form
- .
/* solve */
print(K[0],"*Q=",P[0])$
sol[2] : subst([l[i]=l[0]/I],linsolve_by_lu(K[0],P[0])[1]);
Post-Processing
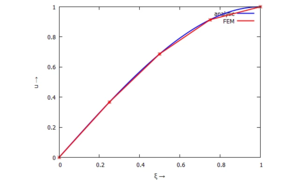
Die Ergebnisse der FE-Rechnung und der analytischen Lösung können wir jetzt übereinander auftragen:
Die Dehnungen (und Spannungen) im Bauteil sind
.
Auch dieses Ergebnis können wir auftragen:
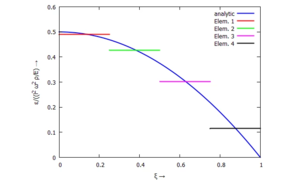
| ✔ Konstante Dehnung je Element: |
| Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element. |
/* post-processing */
U : append([0],args(transpose(sol[2])[1]/subst(params,u[s])));
X : makelist(i,i,0,I)/I;
plot2d([ratsimp(subst([r=xi*l[0]],subst(disp,u(r))/subst(params,u[s]))),
[discrete, X, U],[discrete, X, U]], [xi,0,1],
[legend, "analytic", "FEM", ""],
[style, [lines,2,1], [lines,2,2], [points,2,2]],
[point_type, asterisk],
[xlabel, "ξ →"], [ylabel, "u →"])$
eps: subst(params,u[s])*makelist((U[i+1]-U[i]),i,1,I)/(l[0]/I);
toPlot : append([expand(subst([r=xi*l[0]],diff(subst(disp,u(r)),r))/((l[0]^2*Omega^2*rho)/E))],
makelist([discrete,[i-1,i]/I, [eps[i],eps[i]]/((l[0]^2*Omega^2*rho)/E)],i,1,I));
legends : append([legend, "analytic"],makelist(simplode(["Elem. ",i]),i,1,I));
plot2d(toPlot, [xi,0,1], legends, [y,0,0.6],
[style, [lines,2]],
[xlabel, "ξ →"], [ylabel, "ε/((l^2 ω^2 ρ/E) →"])$
Links
- ...
Literature
- ...