Gelöste Aufgaben

Die Liste von Aufgaben auf dieser Seite ist nicht thematisch sortiert.

Das explizite Lösungsschema für die Bearbeitung der Aufgaben orientiert sich nach einem festen Muster. Grundsätzlich folgen wir dem Standardprozess der Modellbildung. Die meisten Aufgaben sind dafür allerdings zu "klein" und wir adaptieren ein "passendes" Schema.

Bitte orientieren Sie sich an den Schlagworten (Tags) auf der Startseite, wenn Sie Aufgaben zu bestimmten Themen suchen.

COVI

Gesucht ist hier ein phänomenologisches Modell für die Entwicklung der Anzahl der Individuen, die

ansteckbar "a",
infiziert "i" - mit und ohne Sympthome - und
genesen "r"

sind.

DGEB
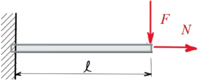	Lageplan. Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab mit Rechteck-Querschnitt unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie δΠ. Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens.

DGEC

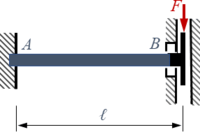Ein Balken AB (Länge ℓ, Rechteck-Querschnitt h*b, Elastizitäts-Module E) ist in A fest eingespannt und in B durch eine Parallelführung gelagert.

In B wird er durch eine senkrechte Kraft F belastet.

Wir vergleichen die Auslenkung in B nach den Balken-Modellen von

Euler-Bernoulli und
Timoshenko

FEAA
	Lageplan Gesucht ist eine Näherungslösung für die statische Auslenkung der beiden Massen für ein System mit einem Freiheitsgrad. Wir arbeiten dabei mit dem Prinzip vom Minimum der Potentiellen Energie und wählen eine Auslenkung als Funktion der zweiten.

FEAB
	Lageplan Gesucht ist die Näherungslösung für die Auslenkung der Stab-Querschnitte mit dem Prinzip der Virtuellen Verrückungen. Wir verwenden polynomialen Ansatzfunktionen über die Gesamtlänge - also eine Mischung aus Finiten-Elemente-Methode und dem Rayleigh-Ritz-Verfahren.

FEAC
	Lageplan Gesucht ist die analytische Lösung für die statische Auslenkung der beiden Massen. Wir arbeiten dabei mit dem Prinzip vom Minimum der Potentiellen Energie.

FEAD
	Lageplan Gesucht ist die Näherungslösung für die statische Auslenkung der Stab-Querschnitte mit dem Prinzip der Virtuellen Verrückungen und dem Ansatz nach der Methode der Finiten Elemente. Dazu wir unterteilen die Struktur in Elemente und setzen Lineare Trialfunctions für die Verformung in den Elemeten an.

FEAE
	Lageplan Gesucht ist Gesamtlösung des Systems im Zeitbereich beim Loslassen der beiden Massen aus der Referenz-Konfiguration, bei der beide Federn entspannt sind. Wir stellen die Bewegungsgleichung mit dem Prinzip der virtuellen Verrückungen auf.

FEAF

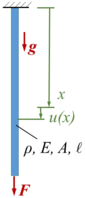
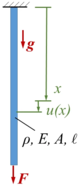
Gesucht ist die Längsschwingung des Stabes beim Loslassen aus seiner unverformten Referenzlage. Dabei arbeiten wir mit der Methode der Finiten Elemente zum Aufstellen der Bewegungsgleichungen. Die Integeationskonstanten der Lösung passen wir an die Anfangsbedingungen

keine Anfangs-Auslenkung
keine Anfangs-Geschwindigkeit

an.

FEAG
	Lageplan Gesucht ist die Schwingung eines Euler-Bernoulli-Balkens beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der Finite Elemente Methode vor, arbeiten also mit dem Prinzip der virtuellen Arbeit.

FEB1
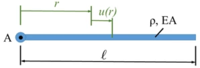	Lageplan Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte.

FEB2
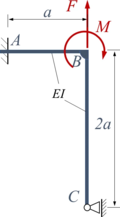	Lageplan Gesucht ist die Verschiebungen und Verdrehungen der Balken mit der Methode der Finiten ELemente.

FEB3
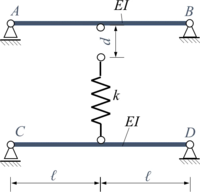	Lageplan. Gesucht sind die Auslenkungen der beiden Verbindungspunkte der Feder mit den Balken. Das Modell soll aus vier Finiten Elementen bestehen, jeweils zwei für die beiden Balken sowie einer Feder.

FEB4
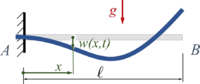
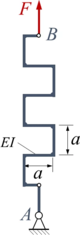	Lageplan Das skizzierte System besteht aus Euler-Bernoulli-Balken (jeweils Länge a) der Biegesteifigkeit EI. Die Konstruktion wird in A durch ein gelenkiges Festlager gehalten und in B durch die Kraft F belastet. Gesucht ist die Ersatzfeder-Steifigkeit des Systems, das Sie aus Finiten Elementen mit Euler-Bernoulli-Balken zusammensetzen.

FEC1
	Turbolader Gesucht ist die homogene Lösung des Differentialgleichungssystems eines Turboladers für verschiedene Drehzahlen. Wir interessieren uns für mögliche Instabilitäten des Systems

FEM1

Using ANSYS workbench, decide upon the wall-thickness of a pressure-vessel subject to a differential internal pressure of p=1 bar. Let

R_{P 0.2} = 2.8 E 8 \frac{N}{m^{2}}; safety factor: s = 2 .

Gelöste Aufgaben

Inhaltsverzeichnis

COVI

DGEB

DGEC

FEAA

FEAB

FEAC

FEAD

FEAE

FEAF

FEAG

FEB1

FEB2

FEB3

FEB4

FEC1

FEM1

Navigationsmenü

Gelöste Aufgaben

Navigationsmenü

Suche