Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik

Arbeits- oder Energieprinzipe der Mechanik basieren auf der Idee, dem Prinzip der "Erhaltung der Energie". Die zentrale Aussage:

Die von Kräften auf der Verschiebung der Kraftangriffspunkte geleisteten Arbeit W^a ist im quasistatischen Fall im Inneren des Körpers als Energie - der Formänderungsenergie Π - gespeichert, also

$W^{a}=\Pi$,

Für eine Einzelkraft auf eine Feder ist

Gleichgewichtsbedingungen mit Arbeitsprinzipen formulieren.

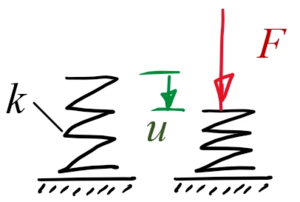::$\displaystyle \Pi ={\frac {1}{2}}\cdot k\cdot u^{2}$ und ${\begin{array}{cl}W^{a}&\displaystyle =\int _{u}{\tilde {F}}({\tilde {u}})\cdot d{\tilde {u}}{\text{ und, da }}\displaystyle {\tilde {F}}=F\cdot {\frac {\tilde {u}}{u}}\\&={\frac {1}{2}}\;F\;u\end{array}}$, also $\displaystyle u={\frac {F}{k}}$,

Mit dieser Aussage allein können wir allerdings kaum etwas anfangen: wir haben nur eine skalare Gleichung für ein ganzes System - egal mit wie vielen Koordinaten (Freiheitsgrade) unser System hat.

Aber auf diesem Prinzip der Erhaltung der Energie bauen wiederum andere Prinzipe auf, die nach den Potentialen der äußeren Kräft und nach der Formänderungsenergie fragen::

• das Sources/Lexikon/Prinzip_vom sagt, dass von allen möglichen Verschiebungszuständen des Systems derjenige die Gleichgewichtslage anzeigt, bei der die Potentielle Energie U des Systems ein Minimum hat - also die Ableitungen von U jeweils nach allen Koordinaten verschwindet. Wir erhalten also je Koordinate eine Gleichung.
• das Prinzip der virtuellen Verrückungen sagt, dass bei einer Variation - oder einem Wackeln an - einem Gleichgewichtszustand des Systems, die Variation der Arbeit - die virtuelle Arbeit des Gesamtsystems - verschwindet. Da die virtuelle Arbeit des Gesamtsystems die Summe der virtuellen Arbeiten auf der Variation der Einzelkoordinaten ist, erhalten wir auch hier genauso viele Gleichungen wie gesuchte Verschiebungen.

Beide haben Ihre Stärken:

• das Prinzip vom Minimum der Potentiellen Energie ist anschaulich, also gut im Rahmen der Didaktik zu gebrauchen. Da es nur bei Systemen funktioniert, deren Kräfte ein Potential haben, scheiden z.B. dynamische Systeme und solche mir Dämpfung aus.
• das Prinzip der virtuellen Verrückungen ist abstrakt und damit schwer anschaulich greifbar, dafür funktioniert es immer.

Es gibt noch weitere Prinzipe wie z.B. die von

• Hamilton
• Hamilton-Ostrogratzki
• Lagrange

Diese sind hier nicht beschreiben.

Weblinks

• Wikipedia: Energy principles in structural mechanics

Untergeordnete Seiten

1. Prinzip der virtuellen Verrückungen
2. Prinzip vom Minimum der Potentiellen Energie

M