Gelöste Aufgaben/W8Zv

Aufgabenstellung

Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:

Caption

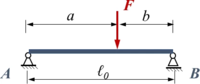
Hier soll mit dem Ansatz mit der Methode der Finiten Elemente gearbeitet werden. Gesucht ist das Verschiebungsfeld w(x) im Vergleich von FEM und analytischer Lösung.

Diese Aufgabe ist eng verwandt mit W8Zt und W8Zu.

Lösung mit Maxima

Mit dem Föppl-Symbol "<>", sowie

$\alpha =a/\ell$, $\beta =1-\alpha$ und $\xi =x/\ell$

ist die analytische Lösung:

$EIw(x)={\frac {\displaystyle F\ell ^{3}}{\displaystyle 6}}\left[\beta \xi (1-\beta ^{2}-\xi ^{2})+<\xi -\alpha >^{3}\right]$.

Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!

Mit den passenden Ansatzfunktionen berechnen wir eine Näherungslösung des Problems nach dem Prinzip der virtuellen Verrückungen.

tmp

Bei der Methode der Finiten Elemente setzen wir die virtuelle Formänderungsenergie des Systems additiv aus den Anteilen je Element zusammen. Hier arbeiten wir mit zwei Elementen, die am Kraft-Angriffspunkt aneinander stoßen.

Also ist

$\delta \Pi =\delta \Pi _{1}+\delta \Pi _{2}$ ,

die virtuelle Arbeit der äußeren Kraft F ist

$\delta W^{a}=F\cdot \delta w_{F}$ .

Header

Text

1+1

tmp

Declarations

Text

1+1

tmp

Aus der Finite Elemente Methode kennen wir die virtuelle Formänderungsenergie eines Balkenelements

$\delta \Pi _{i}=\left(\delta W_{i-1},\delta \Phi _{i-1},\delta W_{i},\delta \Phi _{i}\right)\cdot {\underline {\underline {K}}}_{i}\cdot \left({\begin{array}{l}W_{i-1}\\\Phi _{i-1}\\W_{i}\\\Phi _{i}\end{array}}\right)$

für das klassische x-z-Koordinatensystem des Euler-Bernoulli-Balkens und mit der Element-Steifigkeitsmatrix

$\displaystyle {\underline {\underline {K}}}_{i}={\frac {\mathit {EI}}{{\ell }_{E}^{3}}}\cdot {\begin{pmatrix}12&6\cdot {\ell _{E}}&-12&6\cdot {\ell _{E}}\\6\cdot {\ell _{E}}&4\cdot {\ell _{E}^{2}}&-6\cdot {\ell _{E}}&2\cdot {\ell _{E}^{2}}\\-12&-6\cdot {\ell _{E}}&12&-6\cdot {\ell _{E}}\\6\cdot {\ell _{E}}&2\cdot {\ell _{E}^{2}}&-6\cdot {\ell _{E}}&4\cdot {\ell _{E}^{2}}\end{pmatrix}}$.

Virtual Strain-Energy per Element

Text

1+1

tmp

Das Gesamt-Gleichungssystem für die Koordinaten

${\underline {Q}}=\left({\begin{array}{l}W_{0}\\\Phi _{0}\\W_{1}\\\Phi _{1}\\W_{2}\\\Phi _{2}\end{array}}\right)$

ist

${\underline {\underline {K}}}_{0}\cdot {\underline {Q}}={\underline {P}}$

mit der 6x6 Matrix K₀. In diese Matrix müssen wir jetzt die Element-Steifigkeitsmatrizen für das Element 1 und das Element 2 hineinaddieren, also

${\underline {\underline {K}}}_{0}=EI\cdot {\begin{pmatrix}{\frac {12}{\ell _{1}^{3}}}&{\frac {6}{\ell _{1}^{2}}}&-{\frac {12}{\ell _{1}^{3}}}&{\frac {6}{\ell _{1}^{2}}}&0&0\\{\frac {6}{\ell _{1}^{2}}}&{\frac {4}{\ell _{1}}}&-{\frac {6}{\ell _{1}^{2}}}&{\frac {2}{\ell _{1}}}&0&0\\-{\frac {12}{\ell _{1}^{3}}}&-{\frac {6}{\ell _{1}^{2}}}&{\frac {12}{\ell _{2}^{3}}}+{\frac {12}{\ell _{1}^{3}}}&{\frac {6}{\ell _{2}^{2}}}-{\frac {6}{\ell _{1}^{2}}}&-{\frac {12}{\ell _{2}^{3}}}&{\frac {6}{\ell _{2}^{2}}}\\{\frac {6}{\ell _{1}^{2}}}&{\frac {2}{\ell _{1}}}&{\frac {6}{\ell _{2}^{2}}}-{\frac {6}{\ell _{1}^{2}}}&{\frac {4}{\ell _{2}}}+{\frac {4}{\ell _{1}}}&-{\frac {6}{\ell _{2}^{2}}}&{\frac {2}{\ell _{2}}}\\0&0&-{\frac {12}{\ell _{2}^{3}}}&-{\frac {6}{\ell _{2}^{2}}}&{\frac {12}{\ell _{2}^{3}}}&-{\frac {6}{\ell _{2}^{2}}}\\0&0&{\frac {6}{\ell _{2}^{2}}}&{\frac {2}{\ell _{2}}}&-{\frac {6}{\ell _{2}^{2}}}&{\frac {4}{\ell _{2}}}\end{pmatrix}}$

Weil die Auslenkung des Kraft-Angriffspunktes

$\delta w_{F}=\delta W_{1}$

ist

${\underline {P}}=\left({\begin{array}{c}0\\0\\F\\0\\0\\0\end{array}}\right)$.

Hier fehlen noch die ...

Equilibrium Conditions

Text

1+1

tmp

Einarbeiten der Randbedingungen in die Systemmatrix

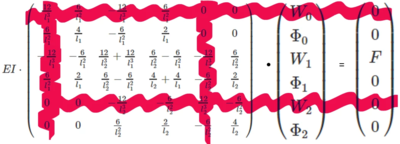
Im Gesamt-Gleichungssystem müssen wir noch die Randbedingungen einarbeiten, nämlich

${\begin{array}{ll}W_{0}=0&(\delta W_{0}=0)\\W_{2}=0&(\delta W_{2}=0)\end{array}}$

Das machen wir durch Streichen der zugehörigen Zeilen und Spalten (1 und 5) im Gleichungssystem.

Boundary Conditions

Text

1+1

tmp

Die Lösung des verbleibenden Gleichungssystems mit

$\displaystyle \alpha ={\frac {a}{\ell _{0}}},\;\;\;\ell _{0}=a+b$

ist

${\begin{array}{ccl}\displaystyle {{\Phi }_{0}}\cdot &\displaystyle {\frac {EI}{{\ell _{0}^{2}}\cdot F}}&\displaystyle ={\frac {2\cdot \alpha -3\cdot {{\alpha }^{2}}+{{\alpha }^{3}}}{6}}\\\displaystyle {{W}_{1}}\cdot &\displaystyle {\frac {EI}{{\ell _{0}^{3}}\cdot F}}&\displaystyle ={\frac {{{\alpha }^{2}}-2\cdot {{\alpha }^{3}}+{{\alpha }^{4}}}{3}}\\\displaystyle {{\Phi }_{1}}\cdot &\displaystyle {\frac {EI}{{\ell _{0}^{2}}\cdot F}}&\displaystyle ={\frac {\alpha -3\cdot {{\alpha }^{2}}+2\cdot {{\alpha }^{3}}}{3}}\\\displaystyle {{\Phi }_{2}}\cdot &\displaystyle {\frac {EI}{{\ell _{0}^{2}}\cdot F}}&\displaystyle ={\frac {{{\alpha }^{3}}-\alpha }{6}}\end{array}}$

Und die Ergebnisse können wir mit der analytischen Lösung vergleichen:

Solve

Text

1+1

tmp

Die Auslenkung des Kraft-Angriffspunktes w(a) tragen wir hier auf:

Absenkung w(a) des Kraftangriffspunktes

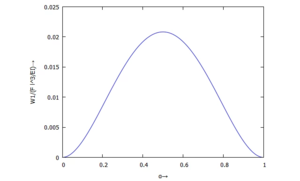
Post-Process: Results

Text

1+1

tmp

Der Vergleich der tabellierten Lösungen mit unseren Lösungen:

Ort	analytische Lösung	FEM-Lösung	Vergleich
A
B
Kraftangriffspunkt

⚠ Ist das jetzt die analytische Lösung?:

Sind die FEM-Ergebnisse nicht exakt die der analytischen Lösung? Stimmt das? Und wenn ja:  wie kommt das?

Post-Process: Compare with Analytic Solution

Text

1+1

---

Links

• W8Zt, W8Zu

Literature

• ...

Lageplan