Gelöste Aufgaben/UEBI

Aufgabenstellung

Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.

In UEBF haben wir eine Näherungslösung für dieses Problem berechnet.

Lageplan

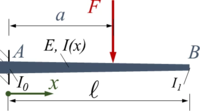
Gesucht ist die analytische Lösung des Problems.

Gegeben sind für den Balken:

• Länge ℓ, Breite b,
• E-Modul E, Dichte ρ und
• die Höhe h₀=b und h₁ jeweils in A und B; dazwischen ist die Höhe linear veränderlich.

Lösung mit Maxima

Um zur analytischen Lösung zukommen, müssen wir berücksichtigen, dass

$E\,I(x)\cdot \displaystyle {\frac {d^{2}}{dx^{2}}}w(x)=-M(x)$.

Wir müssen also hier die Abhängigkeit der Querschnittseigenschaften von "x" in der Differentialbeziehung berücksichtigen. Das macht die Sache deutlich komplizierter als vorher.

Header

Wir haben die Differential-Beziehungen

${\begin{array}{rcl}Q'&=&-q\\M'&=&+Q\\E\,I\cdot \phi '&=&-M\\w'&=&+\phi \end{array}}$

für die Querkraft Q, das Moment M, die Verkippung der Querschnitte ϕ und die Auslenkung w. Dabei ist die ortsabhängige Streckenlast

$q(x)=A(x)\,\rho \,g{\text{ mit }}A(x)=b\cdot h(x).$

Die Höhe des Balkens ist linear veränderlich, nämlich

$h(x)=h_{0}\,(1-\xi )+h_{1}\,\xi {\text{ mit }}\xi =\displaystyle {\frac {x}{\ell }}$.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 18.10.1                           */
/* author: Andreas Baumgart                            */
/* last updated: 2019-09-30                            */
/* ref: TM-C, Balken mit linear-veränderlicher Höhe    */
/* description: finds the analytic solution for        */
/*              problem                                */
/*******************************************************/

/* declare variational variables - see 6.3 Identifiers */
declare( "ℓ", alphabetic);
declare( "ϕ", alphabetic);

Declarations

Diese Abkürzungen führen wir ein:

$\displaystyle m=\rho \,{\frac {h_{0}+h_{1}}{2}}\,b\,\ell \,g$,

$h_{1}=\alpha \,h_{0}$.

Für die Ergebnisse setzten wir dann exemplarisch

$\displaystyle \alpha ={\frac {1}{2}}$

an - sonst werden die Ausdrücke zu umfangreich.

/* make equations of motion dim'less with load case #6 */
reference : [Phi[ref] = W[ref]/ℓ, W[ref] = q[ref]*ℓ^4/(8*E I[ref]), 
             M[ref] = m*g*ℓ, Q[ref] = m*g, 
             q[ref] = m*g/ℓ, EI[ref]=E*b*((H[0]+H[1])/2)^3/12];

/* system parameters                                  */
params: [q[0]  = A(xi)*rho*g,
         A(xi) = b*h(xi),
         I(xi) = b*h(xi)^3/12,
         h(xi) = H[0]*(1-xi)+ H[1]*xi];
params: append(params,
               solve((H[0]+H[1])/2*b*ℓ*rho=m, rho));

geometry : [alpha=1/2];

dimless: [x = xi*ℓ, H[0]=b, H[1]=alpha*b];

sections: [%c4=C[0], %c3=C[1], %c2=C[2], %c1=C[3]];

Dimensionless Form of Differential Equations

Beim Aufintegrieren der Differentialgleichungen stören die vielen dimensionsbehafteten Parameter. Viel einfacher werden die Gleichungen, wenn wir sie in dimensionsloser Form - mit dimensionsloser Auslenkung, Kippwinkel, Biegemoment und Querkraft anschreiben, also

${\begin{array}{lcc}w&=W_{ref}&\cdot &{\tilde {w}}\\\phi &=\Phi _{ref}&\cdot &{\tilde {\phi }}\\M&=M_{ref}&\cdot &{\tilde {M}}\\Q&=Q_{ref}&\cdot &{\tilde {Q}}\end{array}}$.

Wir wählen dazu als Referenzlösung den Kragbalken mit konstantem Querschnitt unter konstanter Streckenlast, mit der maximalen Auslenkung

$W_{ref}=\displaystyle {\frac {q_{ref}\,\ell ^{4}}{8\,E\,I_{ref}}}$.

Als Referenz-Werte für die Streckenlast wählen wir hier die Werte unseres Balkens in x=ℓ/2, demnach

${\begin{array}{ll}q_{ref}&=A_{ref}\,\rho \,g{\text{ mit }}A_{ref}=b\cdot h(\displaystyle {\frac {\ell }{2}})\\I_{ref}&=\displaystyle {\frac {b\cdot h(\displaystyle {\frac {\ell }{2}})^{3}}{12}}\end{array}}$.

Die Differentialgleichungen werden dadurch und mit der dimensionslosen Ortskoordinate

$\xi =\displaystyle {\frac {x}{\ell }}$

viel einfacher, nämlich

${\begin{array}{rcl}\displaystyle {\frac {\partial }{\partial \xi }}{\tilde {Q}}&=&-\displaystyle {\frac {4-2\xi }{3}}\\{\frac {\displaystyle \partial }{\displaystyle \partial \xi }}{\tilde {M}}&=&+{\tilde {Q}}\\{\frac {\displaystyle \partial }{\displaystyle \partial \xi }}{\tilde {\phi }}&=&-{\frac {\displaystyle 8}{\frac {I(\displaystyle \xi )}{\displaystyle I_{ref}}}}\cdot {\tilde {M}}{\text{ mit }}{\frac {\displaystyle I(\xi )}{\displaystyle I_{ref}}}={\frac {\displaystyle (\alpha +1)^{3}}{\displaystyle 8\,((\alpha -1)\,\xi +1)^{3}}}\\{\frac {\displaystyle \partial }{\displaystyle \partial \xi }}{\tilde {w}}&=&+{\tilde {\phi }}\end{array}}$.

Damit es übersichtlicher wird, lassen wir die Tilden über den gesuchten dimensionslosen Funktionen gleich wieder weg.

/******************************************************/
/* Boundary Value Problem Formulation                 */
/* field                                              */

dgl : [        Q[ref]*diff(Q(xi),xi)/ℓ = - q(xi),
               M[ref]*diff(M(xi),xi)/ℓ = + Q[ref]*Q(xi),
       E*I(xi)*diff(Phi[ref]*ϕ(xi),xi)/ℓ = - M[ref]*M(xi),
               diff(W[ref]*w(xi),xi)/ℓ = + Phi[ref]*ϕ(xi)];

dgl: subst(reference,dgl);

Integration Of Differential Equation

Die Differentialbeziehungen lösen wir nun sukzessive zu

$\displaystyle Q(\xi )={\frac {\xi ^{2}-4\xi +3\,C_{3}}{3}}$,

$\displaystyle M(\xi )={\frac {{{\xi }^{3}}-6{{\xi }^{2}}+9{C_{3}}\xi +9{C_{2}}}{9}}$.

Bis hier ist alles wie gehabt - aber jetzt steht das ortsveränderliche Flächenmoment I(ξ) im Nenner. Maxima liefert

$\displaystyle \phi (\xi ))={\frac {6{{\xi }^{3}}+\left(2{C_{1}}-24\right)\,{{\xi }^{2}}+\left(-54{C_{3}}-8{C_{1}}+96\right)\xi +54{C_{3}}-27{C_{2}}+8{C_{1}}-96}{2{{\xi }^{2}}-8\xi +8}}$

und im nächsten Schritt schließlich

$\displaystyle w(\xi )={\frac {3{{\xi }^{3}}+\left(2{C_{1}}-6\right)\,{{\xi }^{2}}+\left(\left(72-54{C_{3}}\right)\ln {\displaystyle \left(-{\frac {\xi -2}{2}}\right)}-4{C_{1}}+2{C_{0}}\right)\xi +\left(108{C_{3}}-144\right)\ln {\displaystyle \left(-{\frac {\xi -2}{2}}\right)}+54{C_{3}}+27{C_{2}}-4{C_{0}}-48}{2\xi -4}}$.

Darin enthalten sind die unbekannten - also gesuchten - Integrationskonstanten

$C_{0},C_{1},C_{2},C_{3}$.

/******************************************************/
/* integrate differential equations                   */
displ : ratsimp(integrate(subst(dimless,ratsimp(subst(params,solve(dgl[1],Q(xi))))),xi));
displ : append(displ, ratsimp(integrate(subst(displ,solve(dgl[2],M(xi))),xi)));
displ : append(displ, ratsimp(
  integrate(
    ratsimp(subst(dimless,subst(geometry,subst(displ, subst(params,solve(dgl[3],'diff(ϕ(xi),xi))))))),xi
        )));
displ : append(displ, ratsimp(
    integrate(
      subst(displ,
        solve(dgl[4],w(xi))
        ),
      xi)));

displ : ratsimp(subst(sections, subst(geometry,displ)));

Boundary Conditions

Diese Unbekannten bestimmen wir aus den Randbedingungen, nämlich

${\begin{array}{rcl}w(0)&=&0\\\phi (0)&=&0\\M(1)&=&0\\Q(1)&=&0\\\end{array}}$

und damit

${\begin{array}{rcl}0&=&C_{3}-1\\0&=&9{C_{3}}+9{C_{2}}-5\\0&=&54{C_{3}}-27{C_{2}}+8{C_{1}}-96\\0&=&-54{C_{3}}-27{C_{2}}+4{C_{0}}+48\end{array}}$.

/******************************************************/
/* part II: boundary conditions                       */
node[A]: [ w(0) = 0,
           ϕ(0) = 0];
node[B]: [ Q(1) = 0,
           M(1) = 0];

BCs : [subst(node[B],subst([xi=1],displ[1])),
       subst(node[B],subst([xi=1],displ[2])),
       subst(node[A],subst([xi=0],displ[3])),
       subst(node[A],subst([xi=0],displ[4]))];
scale: [3, 9, 8, 4];
BCs : expand(ratsimp(scale*BCs));

Solving

Zum Lösen bringen wir die Gleichungen in die Form

${\begin{pmatrix}0&0&0&-3\\0&0&-9&-9\\0&-8&27&-54\\-4&0&27&54\end{pmatrix}}\cdot {\begin{pmatrix}{C_{0}}\\{C_{1}}\\{C_{2}}\\{C_{3}}\end{pmatrix}}={\begin{pmatrix}-3\\-5\\-96\\48\end{pmatrix}}$,

die wir lösen zu

${\begin{array}{lcc}C_{0}&=&-\displaystyle {\frac {3}{2}},\\C_{1}&=&+\displaystyle {\frac {15}{4}},\\C_{2}&=&-\displaystyle {\frac {4}{9}},\\C_{3}&=&+1\end{array}}$.

/* integration constants = unknowns */
X : [C[0],C[1],C[2],C[3]];
ACM: augcoefmatrix(BCs,X);
/* system matrix and rhs */
AA :   submatrix(ACM,5);
bb : - col(ACM,5);
/* print OLE */
print(subst(params,AA),"*",transpose(X),"=",subst(params,bb))$

/******************************************************/
/* solving                                            */
D : ratsimp(determinant(AA))$
[ P, L, U] : ratsimp(get_lu_factors(lu_factor(AA)))$
cc : ratsimp(linsolve_by_lu(AA,bb)[1])$
sol : makelist(X[i] = cc[i][1],i,1,4)$

Post-Processing

Die Ergebnisse schauen wir uns in dimensionsloser Form an, wobei wir die Standard-Lösungen für den Balken unter konstanter Streckenlast ansetzen.

Für

${\begin{array}{lcl}W_{ref}&=&\displaystyle {\frac {q_{ref}\cdot \ell ^{4}}{8EI_{ref}}},\\\Phi _{ref}&=&\displaystyle {\frac {W_{ref}}{\ell }},\\M_{ref}&=&m\cdot g\cdot \ell ,\\Q_{ref}&=&m\cdot g,\\q_{ref}&=&m\cdot g/\ell ,\\EI_{ref}&=&E\cdot \displaystyle {\frac {b\cdot ((H_{0}+H_{1})/2)^{3}}{12}}\end{array}}$

finden wir

• ... für w(ξ):

  

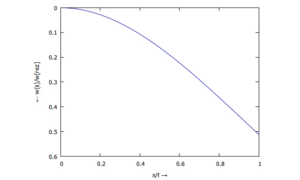
  Auslenkung w(x)

• ... für ϕ(ξ):

  

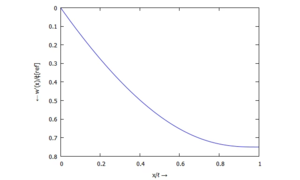
  Querschnitts-Kippung w'(x)

• ... für M(ξ):

  

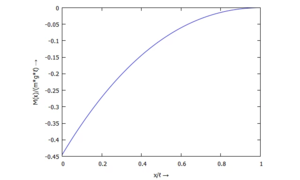
  Momentenverlauf M(x)

• ... für Q(ξ):

  

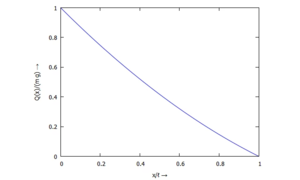
  Querkraftverlauf Q(x)

/******************************************************/
/* post-processing                                    */

/* bearing forces and moments */
reactForces: [M[A] = M[ref]*M(0),
              Q[z] = Q[ref]*Q(0)];
reactForces: ratsimp(subst(sol, subst(subst([xi=0],displ),subst(reference,reactForces))));
 
/* plot displacements */
 
fcts: [ w (xi),
        ϕ (xi),
        M (xi),
        Q (xi)];

textlabels : ["← w(x)/w[rez]", "← w'(x)/ϕ[ref]", "M(x)/(m*g*ℓ) →", "Q(x)/(m g) →"];

for i: 1 thru 4 do(
  f : ratsimp(subst(geometry,subst(sol, subst(geometry,subst(dimless,subst(displ,subst(params,fcts[i]))))))),
  preamble: if i<=2 then "set yrange [] reverse" else "set yrange []",
  plot2d(f, [xi,0,1], [legend, false],
                      [gnuplot_preamble, preamble],
                      [xlabel, "x/ℓ →"],
                      [ylabel, textlabels[i]]) )$

/******************************************************/
/* print tabular values                                             */

for i: 1 thru 4 do(
  f : ratsimp(subst(geometry,subst(sol, subst(geometry,subst(dimless,subst(displ,subst(params,fcts[i])))))*facts[i])),
  N :100,
  print("table for",textlabels[i]),
  for j: 0 thru N do (
    t : j/N,
    print(float(t),";",expand(float(subst([xi=t],f))))
      ))$

Plot Data

---

Links

• Aufgabe UEBF

Literature

• ...