Gelöste Aufgaben/UEBF
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch eine vertikale Einzelkraft F0 belastet. Er ist in A fest eingespannt und hat ein linear veränderliches Flächenmoment I(x).
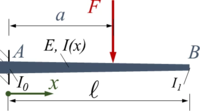
Gesucht ist eine Lösung für die Auslenkung w(x) mit dem Ansatz von Ritz und einer Trial-Funktion.
Damit ähnelt diese Aufgabe UEBC.
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des einseitig fest eingespannten Balkens unter einer Einzellast bei B. Hier ist die maximale Auslenkung
- .
Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken.
Header
Wir berechnen die Potentielle Energie U des Systems und erhalten aus
die Gleichung für den gesuchten Koeffizienten W der Trial-Funktion.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-02-13 */
/* ref: TMC */
/* description: Rayley-Ritz-Solution for EBB */
/* with I(x) */
/*******************************************************/
Declarations
Zum Dimensionslos-Machen der Gleichungen wählen wir
- .
/* make equations of motion dim'less with load case #1 from Gross e.a. */
dimless: [W[a] = F*l^3/(3*E*I[1]),
x=xi*l,
a=alpha*l];
/* parameter */
params: [I(xi) = I[0]*(1-xi)+I[1]*xi];
Formfunctions
Gesucht ist hier ein Ansatz mit einer einzigen Trial Function, also
und dem gesuchten Koeffizienten W. ϕ muss dabei alle geometrischen Randbedingungen erfüllen:
Die Funktionen müssen nicht die Randbedingungen für Schnittlasten in B erfüllen - schließlich suchen wir nach einer Näherungslösung!
Diese Funktion ϕ zu konstruieren ist einfach: wir brauchen lediglich eine doppelte Nullstelle in x=0, also z.B.
- .
Der freie Koeffizient W ist nun die Auslenkung in B - deshalb taufen wir ihn hier WB. Wir wählen ihn so, dass Sie die exakte Lösung bestmöglich approximiert.
/* trial function */
trial: [w(xi) = W[B]*xi^2];
Potential Energy
Für die Gleichgewichtsbedingungen setzten wir Π (aus Abschnitt Euler-Bernoulli-Balken) und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir
berücksichtigen und erhalten
- .
Weil wir in der Spaltenmatrix
nur eine Unbekannte WB haben, können wir es uns hier etwas einfacher machen, U lautet:
- .
/* potential energies */
/* define potential energy of system */
PMPE : [U = Pi - A,
Pi = 1/2*l*'integrate(E*I(xi)*'diff(w(xi),xi,2)^2/l^4,xi,0,1),
A = F*w(alpha)];
PMPE: subst([w(alpha) = subst([xi=a/l],subst(trial,w(xi)))],
subst(params, subst(trial,
subst(PMPE[3],subst(PMPE[2], PMPE[1])))));
PMPE : ev(PMPE,nouns);
Equilibrium Conditions
Diese Gleichung erfüllt die Gleichgewichtsbedingung(en)
- ,
wenn
- .
/* equilibreium condition */
equilibrium : diff(subst(PMPE, U),W[B]) = 0;
Solving
Auflösen nach WB liefert
- .
/* solve */
sol: solve(equilibrium,W[B]);
Post-Processing
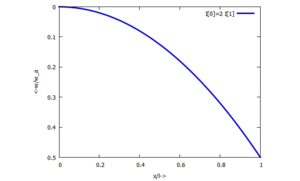
Und so sieht die normierte Absenkung des Punktes B als Funktion von a aus:
Dies ist nicht die Biegelinie des Balkens!
Aufgabe UEBD zeigt, wie wir zu einer besseren Approximation kommen.
| ✔ Schnittmomenten-Verlauf: |
| Probieren Sie aus, wie gut der Ritz-Ansatz den Verlauf des Schnittmoments approximiert! |
/* post-processing */
plot2d(subst([I[0]=2*I[1]],subst(dimless,subst(sol,W[B]/W[A]))),[alpha,0,1],
[gnuplot_preamble, "set yrange [] reverse"],
[legend, "I[0]=2 I[1]"],
[xlabel, "x/l->"], [ylabel, "<-w/w_a"],
[style, [lines,3]]);
Links
Literature
- ...