Gelöste Aufgaben/Kw56

Aufgabenstellung

Die Aufgabenstellung ist identisch mit Aufgabe Kw55, hier ist die Lösung mit dem Verfahren von Rayleigh-Ritz gefragt.

Lageplan

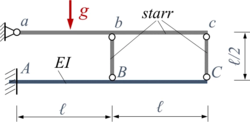
Gesucht ist eine Näherungslösung mit dem Verfahren von Rayleigh-Ritz für ein Euler-Bernoulli-Modell der Struktur.

Verwenden Sie zwei freie Trial-Funtions.

tmp

Die Herausforderung der Aufgabe liegt wieder in der kinematischen Zwangsbedingung, die der starre Stab abc dem Euler-Bernoulli-Balken auferlegt. Diese Zwangsbedingung lautet

$w_B=\frac{1}{2}{w}_C$,

mit den Abkürzungen

• w_B = w( ℓ),
• 'w_C= w(2ℓ).'

Die geometrischen Randbedingungen in A erfüllen wir, indem wir Polynome ab dem Grad 2 verwenden.

Für die Lösung nach Rayleigh-Ritz können wir

• zwei freie Trial-Functions wählen, die die Zwangsbedingung selbst schon erfüllen
• mit Lagrange-Multiplikator die Zwangsbedingung einbauen.

Der zweite Weg ist bei Computer-Anwendungen meist viel einfacher - den gehen wir hier.

Header

Text

1+1

tmp

Wir brauchen

$q_0=\frac{mg}{\ell }$

und nutzen eine Referenzlösung (wie in Kw55)

$\begin{array}{ccc}\hat{w}& =& \frac{q_0(2\ell {)}^4}{8EI}\\ \hat{\varphi }& =& \frac{q_0(2\ell {)}^3}{6EI}\end{array}$.

Declarations

Text

1+1

tmp

Um zwei freie Trial-Functions zu bekommen, müssen wir drei ansetzen: ein Freiheitsgrad wird von der kinematischen Zwangsbedingung aufgehoben.

Also wählen wir

$w(\xi )=\hat{w}\cdot \sum _{i=2}^4{W}_i\cdot {\xi }^i$

mit

$x=\xi \cdot \ell$

und ergänzen dies um die Zwangsbedingung

$2\cdot w(1)=w(2)$.

Achtung: Der Balken ist "2"-lang.

Formfunctions

Text

1+1

tmp

Für die Gleichgewichtsbedingungen brauchen wir die potentielle Energie (hier die Lagrange-Funktion)

$\begin{array}{lcl}\mathrm{\Lambda }=& & \frac{1}{2\cdot {\ell }^3}EI\underset{0}{\overset{2}{\int }}{(\frac{d^2}{d{\xi }^2}\cdot w(\xi ))}^{2}d\xi \\ & -& (2mg+\frac{1}{2}mg)\cdot w(1)+\left(\frac{1}{2}mg\right)\cdot w(2)\\ & +& \lambda \cdot \frac{m^2{g}^2{\ell }^3}{EI}\cdot (2w(1)-w(2))\end{array}$

wobei der konstante Faktor bei dem Lagrange-Multiplikator λ nur der Ästhetik dient ....

Die gesuchten Größen sind nun

$\underset{\_}{Q}=\left(\begin{array}{c}{W}_2\\ W_3\\ W_4\\ \lambda \end{array}\right)$,

und die Gleichgewichtsbedingungen kommen aus

$\frac{d\mathrm{\Lambda }}{d{Q}_i}\stackrel{!}{=}0$

zu

$\begin{array}{cc}-2\lambda +256W_4+96W_3+32W_2-1& =0,\\ -2\lambda +384W_4+128W_3+32W_2+1& =0,\\ 70\lambda -18432W_4-5760W_3-1280W_2-55& =0,\\ -7W_4-3W_3-W_2& =0\end{array}$.

Equilibrium Conditions

Text

1+1

tmp

Dieses lineare Gleichungssystem hat die Lösung

$W_2=\frac{23}{56},W_3=-\frac{27}{112},W_4=\frac{5}{112},\lambda =\frac{3}{14}$

Solving

Text

1+1

tmp

Verläufe der gesuchten Größen

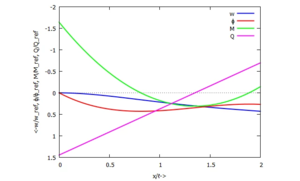
Einsetzen in die Trial-Functions liefert die (dimensionslosen) Funktionsverläufe für w, ϕ, M und Q:

Post-Processing

Text

1+1

---

Links

• ...

Literature

• ...