Gelöste Aufgaben/Kw52

Aufgabenstellung

Eine Brücke ABC der Masse m_B und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit K_C mit dem Lager verbunden. In A steht eine Person der Masse m_A.

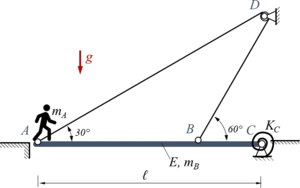
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Ansatz der Finiten Elemente an.

Dies ist eine Näherungslösung zu Kw50. Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:

${\begin{array}{ll}K_{C}=&\displaystyle 5{\frac {E\,I}{\ell _{0}}}\\m_{A}=&\displaystyle {\frac {m_{B}}{5}}\end{array}}$

Lösung mit Maxima

In dieser Aufgabe berechnen wir eine Näherungslösung nach dem Prinzip der virtuellen Verrückungen. Alle Überlegungen zur Geometrie des Systems übernehmen wir aus Kw50.

Für die Lösung nutzen wir direkt die Elemente aus der FEM-Formulierung für den Euler-Bernoulli-Balken.

Text

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 18.10.1                           */
/* author: Andreas Baumgart                            */
/* last updated: 2019-02-12                            */
/* ref: TM-C, Labor 4, FEM-solution                    */
/* description: finds the FEM solution for             */
/*              lab problem with geometric constraints */
/*******************************************************/

Declarations

Wir arbeiten mit den selben Parametern und Bezugslängen, wie in Kw50.

/* declare variational variables - see 6.3 Identifiers */
declare( "δW", alphabetic); 
declare( "δΦ", alphabetic); 
declare(  "Φ", alphabetic); 
declare( "δw", alphabetic); 
declare( "δϕ", alphabetic);
declare( "δΠ", alphabetic); /* elastic potential */
declare( "ϕ" , alphabetic);
declare( "Δs", alphabetic);
declare( "ℓ" , alphabetic);

/* system parameters                                  */
params: [K[C]     = kappa*EI/ℓ[0],
         q[0]     = m[B]*g/ℓ[0],
         m[A]     = theta*m[B],
         theta    = 1/5,
         kappa    = 5];

geometry: [alpha[A] = 30*%pi/180,
           alpha[B] = 60*%pi/180,
           ℓ[1]     = ℓ[0]-ℓ[2],
           Δs[A]    = W[A]*cos(%pi/2-alpha[A]),
           Δs[B]    = W[B]*cos(%pi/2-alpha[B]),
           tan(alpha[B]) = H/ℓ[2],
           tan(alpha[A]) = H/ℓ[0],
           xi[1]    = ℓ[1]/ℓ[0],
           xi[2]    = ℓ[2]/ℓ[0]];
geometry: ratsimp(solve(geometry,[alpha[A],alpha[B],ℓ[1],ℓ[2],Δs[A],Δs[B],H,xi[1],xi[2]])[1]);

/* reference length selected:                         */
dimless : ℓ[Bez] = 1/3*m[B]*g*ℓ[0]^3/(EI); /*cantilevered*/

Formfunctions

Wir nutzen zwei Finite Elemente für die Brücke und setzen dafür die klassischen Hermite-Polynome, i.e. Polynome dritten Grades, an.

An den drei Knotenpunkten A, B und C haben wir also zusammen die Koordinaten

{\underline {Q}}=\left({\begin{array}{c}W_{A}\\\Phi _{A}\\W_{B}\\\Phi _{B}\\W_{C}\\\Phi _{C}\end{array}}\right)

.

/******************************************************/
/* Boundary Value Problem                             */
/* FEM Formulation                                    */

ϕ : [(xi−1)^2*(2*xi+1),
     ℓ[i]*xi*(xi−1)^2,
     xi^2*(3−2*xi),
     ℓ[i]*xi^2*(xi−1)];

Equilibrium Conditions

Für die Gleichgewichtsbedingung

{\begin{array}{lll}\delta W&=&\delta W^{a}-\delta \Pi \\&{\stackrel {!}{=}}&0\end{array}}

konstruieren wir - ohne Berücksichtung der geometrischen Zwangsbedingungen -

\delta \Pi =\delta {\underline {Q}}^{T}\cdot {\underline {\underline {K}}}_{0}\cdot {\underline {Q}}+K_{C}\;\Phi _{C}\;\delta \Phi _{C}

mit

{\underline {\underline {K}}}_{0}=EI\cdot {\begin{pmatrix}{\frac {12}{{\ell }_{1}^{3}}}&{\frac {6}{{\ell }_{1}^{2}}}&-{\frac {12}{{\ell }_{1}^{3}}}&{\frac {6}{{\ell }_{1}^{2}}}&0&0\\{\frac {6}{{\ell }_{1}^{2}}}&{\frac {4}{\ell _{1}}}&-{\frac {6}{{\ell }_{1}^{2}}}&{\frac {2}{\ell _{1}}}&0&0\\-{\frac {12}{{\ell }_{1}^{3}}}&-{\frac {6}{{\ell }_{1}^{2}}}&{\frac {12{{\ell }_{2}^{3}}+12{{\ell }_{1}^{3}}}{{{\ell }_{1}^{3}}\,{{\ell }_{2}^{3}}}}&-{\frac {6{{\ell }_{2}^{2}}-6{{\ell }_{1}^{2}}}{{{\ell }_{1}^{2}}\,{{\ell }_{2}^{2}}}}&-{\frac {12}{{\ell }_{2}^{3}}}&{\frac {6}{{\ell }_{2}^{2}}}\\{\frac {6}{{\ell }_{1}^{2}}}&{\frac {2}{\ell _{1}}}&-{\frac {6{{\ell }_{2}^{2}}-6{{\ell }_{1}^{2}}}{{{\ell }_{1}^{2}}\,{{\ell }_{2}^{2}}}}&{\frac {4{\ell _{2}}+4{\ell _{1}}}{{\ell _{1}}\,{\ell _{2}}}}&-{\frac {6}{{\ell }_{2}^{2}}}&{\frac {2}{\ell _{2}}}\\0&0&-{\frac {12}{{\ell }_{2}^{3}}}&-{\frac {6}{{\ell }_{2}^{2}}}&{\frac {12}{{\ell }_{2}^{3}}}&-{\frac {6}{{\ell }_{2}^{2}}}\\0&0&{\frac {6}{{\ell }_{2}^{2}}}&{\frac {2}{\ell _{2}}}&-{\frac {6}{{\ell }_{2}^{2}}}&{\frac {4}{\ell _{2}}}\end{pmatrix}}

und

\delta W^{a}=\delta {\underline {Q}}^{T}\cdot {\underline {P}}_{0}+m_{A}\,g\;W_{A}\;\delta W_{A}

mit

\displaystyle {\underline {P}}_{0}={\frac {{q_{0}}\,{\ell _{1}}}{2}}\cdot {\begin{pmatrix}{\frac {2{m_{A}}g+{q_{0}}\,{\ell _{1}}}{{q_{0}}\,{\ell _{1}}}}\\{\frac {\ell _{1}}{6}}\\{\frac {{\ell _{2}}+{\ell _{1}}}{\ell _{1}}}\\{\frac {{{\ell }_{2}^{2}}-{{\ell }_{1}^{2}}}{6{\ell _{1}}}}\\{\frac {\ell _{2}}{\ell _{1}}}\\-{\frac {{\ell }_{2}^{2}}{6{\ell _{1}}}}\end{pmatrix}}

.

/* Virtual Strain Energie and Virtual Work of Gravitational Loads  */
K[i] : EI/ℓ[i]^3*makelist(makelist(integrate(diff(ϕ[i],xi,2)*diff(ϕ[j],xi,2),xi,0,1),j,1,4),i,1,4);
P[i] : q[0]*ℓ[i]*makelist(integrate(ϕ[i],xi,0,1),i,1,4);

K[0] : zeromatrix(6,6);
P[0] : zeromatrix(6,1);
for ele: 1 thru 2 do
  (ref : 2*(ele-1),
   for row :1 thru 4 do
      (P[0][ref+row]: P[0][ref+row] + subst([i=ele],P[i][row]),
       for col :1 thru 4 do
           K[0][ref+row][ref+col] : K[0][ref+row][ref+col] + subst([i=ele],K[i][row][col])));
K[0][6,6] : K[0][6,6] + K[C]; 

Q[0] : [[ W[A], Φ[A], W[B], Φ[B], W[C], Φ[C]],
        [δW[A],δΦ[A],δW[B],δΦ[B],δW[C],δΦ[C]]];

δW[0] : Q[0][2].P[0] - Q[0][2].K[0].transpose(Q[0][1]);

Geometric Constraints

Die Bewegung unserer Brücke in durch zwei geometrische Zwangs-Bedingungen behindert:

durch das Lager in C:
$W_{C}=0{\text{ bzw. }}\delta W_{C}=0$ sowie
durch das Seil über die Umlenkrolle in D:
$W_{A}=-{\sqrt {3}}\;W_{B}{\text{ bzw. }}\delta W_{A}=-{\sqrt {3}}\;\delta W_{B}$ .

Diese Bedingungen arbeiten wir in die virtuellen Arbeiten des Systems ein und erhalten dann mit den verbleibenden gesuchten Größen

{\underline {\tilde {Q}}}=\left({\begin{array}{c}\Phi _{A}\\W_{B}\\\Phi _{B}\\\Phi _{C}\end{array}}\right)

das Gleichungssystem

{\mathit {EI}}{\begin{pmatrix}-{\frac {6}{\ell _{0}}}&{\frac {{{3}^{\frac {7}{2}}}+27}{2{{\ell }_{0}^{2}}}}&-{\frac {3}{\ell _{0}}}&0\\{\frac {{{3}^{\frac {7}{2}}}+27}{2{{\ell }_{0}^{2}}}}&-{\frac {{{3}^{\frac {9}{2}}}+486}{{\ell }_{0}^{3}}}&{\frac {{{3}^{\frac {7}{2}}}-81}{2{{\ell }_{0}^{2}}}}&-{\frac {54}{{\ell }_{0}^{2}}}\\-{\frac {3}{\ell _{0}}}&{\frac {{{3}^{\frac {7}{2}}}-81}{2{{\ell }_{0}^{2}}}}&-{\frac {18}{\ell _{0}}}&-{\frac {6}{\ell _{0}}}\\0&-{\frac {54}{{\ell }_{0}^{2}}}&-{\frac {6}{\ell _{0}}}&-{\frac {17}{\ell _{0}}}\end{pmatrix}}{\begin{pmatrix}{{\Phi }_{A}}\\{W_{B}}\\{{\Phi }_{B}}\\{{\Phi }_{C}}\end{pmatrix}}={m_{B}}\,g{\begin{pmatrix}-{\frac {\ell _{0}}{27}}\\-{\frac {5{\sqrt {3}}-16}{10{\sqrt {3}}}}\\{\frac {\ell _{0}}{36}}\\{\frac {\ell _{0}}{108}}\end{pmatrix}}

.

/* Geometric Constraints  */
constraint : append(solve(subst(geometry,Δs[A]+Δs[B]=0), W[A]),[W[C]=0]);
constraint : append(constraint, subst([W[A]=δW[A],W[B]=δW[B],W[C]=δW[C]],constraint));

δW[0] : expand(subst(constraint,δW[0]))$

Q[M] : [[ Φ[A], W[B], Φ[B], Φ[C]],
        [δΦ[A],δW[B],δΦ[B],δΦ[C]]];

eom : makelist(coeff(δW[0],Q[M][2][i]),i,1,length(Q[M][2]));
K[M] : funmake('matrix,makelist(makelist(coeff(eom[i],Q[M][1][j],1),j,1,length(Q[M][1])),i,1,length(eom)));
P[M] : -transpose(expand(funmake('matrix,[eom]) - transpose(K[M].transpose(Q[M][1]))));

K[M] : subst(params, subst(geometry, K[M]));
P[M] : subst(params, subst(geometry, P[M]));

print(EI,ratsimp(K[M]/EI),transpose(Q[M][1])," = ",m[B]*g, ratsimp(P[M]/(m[B]*g)))$

c : (EI/ℓ[0]^3);
K[M] : ratsimp(K[M]/c);
P[M] : ratsimp(P[M]/c);

tmp

Solving

Das Lösen des Gleichungssystems liefert dann

$\displaystyle \left({\begin{array}{c}W_{A}\\\Phi _{A}\\W_{B}\\\Phi _{B}\\W_{C}\\\Phi _{C}\end{array}}\right)={\frac {m_{B}\,g\,\ell _{0}^{3}}{3\;EI}}\left({\begin{array}{l}+0.00291\\+0.01169{\frac {1}{\ell _{0}}}\\-0.00168\\-0.00704{\frac {1}{\ell _{0}}}\\+0\\+0.006198{\frac {1}{\ell _{0}}}\end{array}}\right)$ .

/* Solving ....... */
sol: expand(float(linsolve_by_lu(K[M],P[M])))[1];
sol : makelist( Q[M][1][i] = sol[i][1],i,1,length(Q[M][1]));
sol : makelist( Q[0][1][i] = subst(sol,subst(constraint,subst([W[C]=0],Q[0][1][i]))),i,1,length(Q[0][1]));

Post-Processing

Und die Ergebnisse können wir uns anschauen ...

... für w(x):

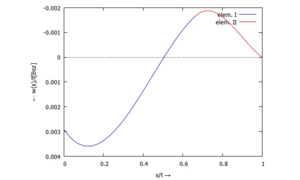
... für Φ(x):

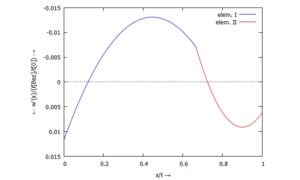
... für M(x):

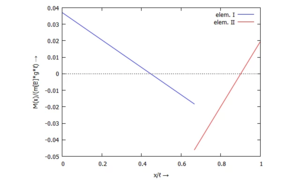
... für Q(x):

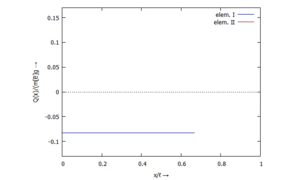
/* Post-Processing                                        */
w : subst(geometry,
                   subst(sol,[subst([i=1],sum(Q[0][1][  j]*ϕ[j],j,1,4)),
                              subst([i=2],sum(Q[0][1][2+j]*ϕ[j],j,1,4))] ));

fcts: [         w     ,
           diff(w,xi  )/[ℓ[1],ℓ[2]],
       -EI*diff(w,xi,2)/[ℓ[1]^2,ℓ[2]^2],
       -EI*diff(w,xi,3)/[ℓ[1]^3,ℓ[2]^3]];
fcts: float(subst(geometry,expand(fcts)))$ 
facts: [1/ℓ[Bez], ℓ[0]/ℓ[Bez], 1/(m[B]*g*ℓ[0]), 1/(m[B]*g)];
 
textlabels : ["← w(x)/ℓ[Bez]", "← w'(x)/(ℓ[Bez]/ℓ[0]) →", "M(x)/(m[B]*g*ℓ) →", "Q(x)/(m[B]g →"];
r : subst(geometry,xi[1]);
for i: 1 thru 4 do(
  f : expand(subst(dimless,facts[i]*fcts[i])),
  preamble: if i<=2 then "set yrange [] reverse" else "set yrange []",
  plot2d([[parametric,       r*t, subst(t,xi,f[1]), [t,0,1]],
          [parametric, r+(1-r)*t, subst(t,xi,f[2]), [t,0,1]]],
                             [legend, "elem. I", "elem. II"],
                             [gnuplot_preamble, preamble],
                             [xlabel, "x/ℓ →"],
                             [ylabel, textlabels[i]]))$

Links

Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)

Literature

...

Gelöste Aufgaben/Kw52

Inhaltsverzeichnis

Aufgabenstellung

Lösung mit Maxima

Für die Lösung nutzen wir direkt die Elemente aus der FEM-Formulierung für den Euler-Bernoulli-Balken.

Declarations

Formfunctions

Equilibrium Conditions

Geometric Constraints

tmp

Solving

Post-Processing

... für w(x):

... für Φ(x):

... für M(x):

... für Q(x):

Navigationsmenü

Gelöste Aufgaben/Kw52

Aufgabenstellung

Lösung mit Maxima

Für die Lösung nutzen wir direkt die Elemente aus der FEM-Formulierung für den Euler-Bernoulli-Balken.

Declarations

Formfunctions

Equilibrium Conditions

Geometric Constraints

tmp

Solving

Post-Processing

... für w(x):

... für Φ(x):

... für M(x):

... für Q(x):

Navigationsmenü

Suche