Gelöste Aufgaben/Kw52
Aufgabenstellung
Eine Brücke ABC der Masse mB und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit KC mit dem Lager verbunden. In A steht eine Person der Masse mA.
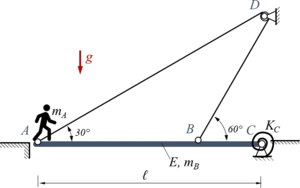
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Ansatz der Finiten Elemente an.
Dies ist eine Näherungslösung zu Kw50. Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Lösung mit Maxima
Für die Lösung nutzen wir direkt die Elemente aus der FEM-Formulierung für den Euler-Bernoulli-Balken.
tmp
Header
Text
1+1
tmp
Wir arbeiten mit den selben Parametern und Bezugslängen, wie in Kw50.
Declarations
Text
1+1
tmp
Wir nutzen zwei Finite Elemente für die Brücke und setzen dafür die klassischen Hermite-Polynome, i.e. Polynome dritten Grades, an.
An den drei Knotenpunkten A, B und C haben wir also zusammen die Koordinaten
.
Formfunctions
Text
1+1
tmp
Für die Gleichgewichtsbedingung
konstruieren wir - ohne Berücksichtung der geometrischen Zwangsbedingungen -
mit
und
mit
.
Equilibrium Conditions
Text
1+1
tmp
Die Bewegung unserer Brücke in durch zwei geometrische Zwangs-Bedingungen behindert:
- durch das Lager in C:
sowie
- durch das Seil über die Umlenkrolle in D:
.
Diese Bedingungen arbeiten wir in die virtuellen Arbeiten des Systems ein und erhalten dann mit den verbleibenden gesuchten Größen
das Gleichungssystem
.
Geometric Constraints
Text
1+1
tmp
Das Lösen des Gleichungssystems liefert dann
.
Solving
Text
1+1
tmp
Und die Ergebnisse können wir uns anschauen ...
... für w(x):
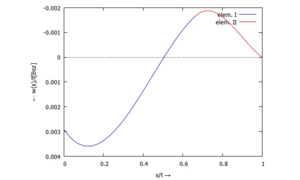
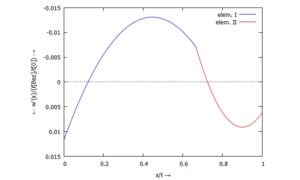
... für Φ(x):
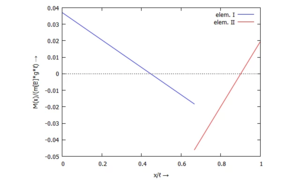
... für M(x):
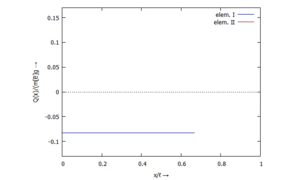
... für Q(x):
Post-Processing
Text
1+1
Links
- Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
- Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
- Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)
Literature
- ...