Gelöste Aufgaben/Kw51
Aufgabenstellung
Eine Brücke ABC der Masse mB und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit KC mit dem Lager verbunden. In A steht eine Person der Masse mA.
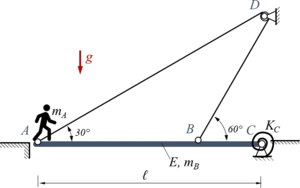
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Verfahren von Rayleigh-Ritz (EBB) an - hier mit Lagrange-Multiplikator für die geometrische Zwangsbedingung.
Dies ist eine Näherungslösung zu Kw50.
Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Lösung mit Maxima
In dieser Aufgabe berechnen wir eine Näherungslösung nach dem Verfahren von Rayleigh-Ritz (EBB) zu Kw50.
Alle Überlegungen zur Geometrie des Systems übernehmen wir.
tmp
Für die Lösung nutzen wir hier das Ritz-Verfahren mit einer Variante:
- die geometrische Zwangsbedingung für die Punkte A, B durch das Seil erfassen wir durch einen Lagrange-Multiplikator.
Header
Text
1+1
tmp
Wir arbeiten mit den selben Parametern und Bezugslängen, wie in Kw50.
Insbesondere gilt auch hier wieder
.
Declarations
Text
1+1
tmp
Nach "Ritz" wählen wir Trial-Functions über die gesamte Stablänge und müssen uns überlegen, welchen Aufwand wir dafür treiben wollen.
Intuitiv wählen wir für jeden Punkt A, B, C jeweils eine Koordinate, hier
.
und brauchen - zusammen der geometrischen Randbedingung w(ℓ)=0 ein Polynom mit vier freien Parametern - also ein Polynom dritten Grades.
Mit dem Ansatz für die Formfunktion
kommt aus den Bedingungen oben dann
mit
.
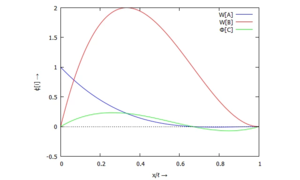
Und so sehen sie aus, unsere drei Trial-Functions:
Für die Formfunktion gilt aber immer die geometrische Zwangsbedingung:
Formfunctions
Text
1+1
tmp
Die Potentiale aus Elastischer Energien und Arbeitsfunktion der Gewichtskräfte sind
.
Nach dem Prinzip vom Minimum der Potentiellen Energie ist das System im Gleichgewicht, wenn das Potential U des Systems
erfüllt. Und sich zusätzlich an die Zwangsbedingung hält!
Equilibrium Conditions
Text
1+1
tmp
Das könnten wir mit dem Konzept der Lagrange-Multiplikatoren erfassen. Dafür schreiben wir
mit dem Lagrange-Multiplikator λ. Die neuen Gleichgewichtsbedingungen lauten nun
und wir erhalten die vier Gleichungen
.
Geometric Constraints
Text
1+1
tmp
Das Lösen des Gleichungssystems liefert dann
.
Solving
Text
1+1
tmp
Und die Ergebnisse können wir uns anschauen ...
... für w(x):
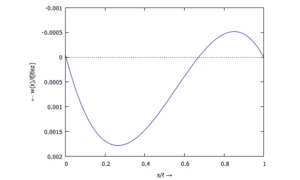
... für Φ(x):
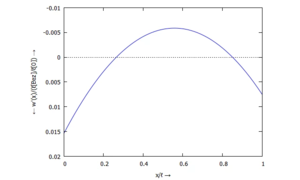
... für M(x):
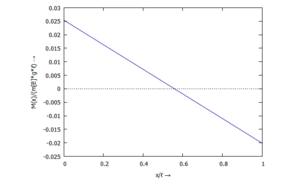
... für Q(x):
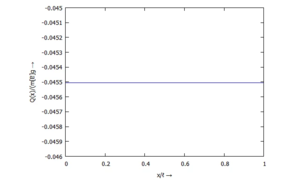
Post-Processing
Text
1+1
Links
- Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
- Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
- Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)
Literature
- ...