Gelöste Aufgaben/JUMP/E-Motor and Drive-Train

Scope

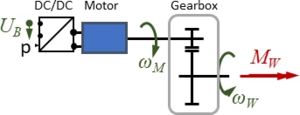
The Drive-Train consists of a DC/DC-converter, a DC Motor and a gear-box.

DC/DC-converter: is supplied with the battery voltage U_B, the output voltage is controlled by the driver via setpoint “p“.
motor: is a standard DC brushed motor, the manufacturer provides only few information on its characteristics - we’ll need to improvise.
gearbox: has a gear ratio of ratio of n_G=100, its shaft rotates at speed ω_W and delivers a torque M_W to the front wheels.

The task is: provide a mathematical model for the drive train that accounts for load-alterations imposed by the driver. And we assume losses in the two converters - DC/DC and gearbox - to be negligible.

Structure

The drive train receives a "gas"-pedal position "p" from the driver and a battery-voltage U_B.

It delivers a torque M_W on the wheel and creates an electric current I_M through the motor.

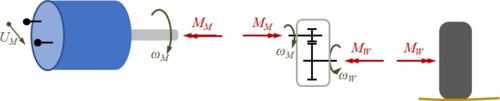
The sub-model consists of DC/DC-converter, Motor and gear-box:

DC/DC Converter

Losses in the DC/DC converter shall be small - so for input port “1“ and output port “2“ we obtain

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_B \cdot I_B = U_M \cdot I_M} .

Let the “gas”-pedal-indicator “p“ control

U_{M}=p\cdot U_{B}{\text{; }}0\leq p\leq 1.

with

0\leq p\leq 1{\text{ and }}U_{1}=U_{B}

Motor

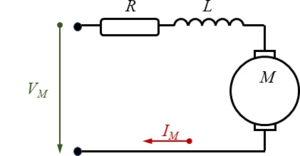
We use a common electric circuit representation for a series wound motor, the field coils are connected electrically in series with the armature coils, resistance R sums up all electrical losses in the motor.

Gearbox

Losses in the gearbox shall be small - so for input (ω_M, M_M) and output (ω_W, M_W) we obtain the fixed relation

\omega _{M}\cdot M_{M}=\omega _{W}\cdot M_{W}

.

Fortunately, this relationship is already "hardwired" in the Principle of Virtual Work. And we have only one differential equation for the electrical components:

{\frac {\displaystyle dI_{B}}{\displaystyle dt}}={\frac {\displaystyle U_{L}}{\displaystyle L}}

,

the remaining equations are algebraic.

Model

Electrical Components

For the motor, we find with Kirchhoff's law that

U_{M}=U_{R}+U_{L}+e

with U_R, U_L being the differential voltage over resistance R and inductance L respectively. “e” is the back electromagnetic force with

e=k_{e}\cdot {\tilde {\omega }}_{M}

and the electromotive force constant k_e. Note the ${\tilde {\omega }}_{M}$ is the differential rotational velocity between rotor and stator, i.e.

{\tilde {\omega }}_{M}={\dot {\psi }}_{M}(t)-{\dot {\phi }}(t).

Employing

U_{R}=R\cdot I_{M},U_{L}=L\cdot {\frac {\displaystyle dI_{M}}{\displaystyle dt}}

and using

M_{M}=k_{T}\cdot I_{M}

with the armature constant k_T, we have the complete set of equations.

From the above, we find

L\cdot {\frac {\displaystyle d}{\displaystyle dt}}{I_{M}}(t)=U_{B}(t)\cdot p(t)-R\,{I_{M}}(t)-e

and additionally the algebraic equations

{\begin{array}{ll}{I_{B}}&={I_{M}}\cdot \operatorname {p} (t),\\{U_{R}}&=R\cdot {I_{M}}(t),\\{U_{L}}&={U_{B}}\cdot \operatorname {p} (t)-R\cdot {I_{M}}(t)-e,\\{U_{M}}&={U_{B}}\cdot \operatorname {p} (t)\end{array}}

.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 16.04.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2021-02-08                            */
/* ref: Modelling and Simulation (TUAS)                */
/* description: virtual work of drive train electrics  */
/*******************************************************/

/*******************************************************/
/* declarations                                        */
/*******************************************************/
declare("φ", alphabetic);
declare("ψ", alphabetic);
declare("ω", alphabetic);

/*******************************************************/
/* kinematics                                          */
/*******************************************************/
kirchhoff : [U[M] = p(t)*U[B],
	     U[B]*I[B] = U[M]*I[M],
	     U[M] = U[R] + U[L] + e,
             e = k[e]*omega[M],
	     ω[M] = diff(ψ[M](t),t)+diff(φ(t),t),
	     U[R] = R*I[M](t),
	     U[L] = L * diff(I[M](t),t),
	     M[M] = k[t]*I[M](t)];

solve(kirchhoff[7], [diff(I[M](t),t)]);

Mechanical Components

The Virtual Work of d'Alembert forces, motor torque M_M and wheel torque M_W is

{\begin{array}{ll}\delta W&=-J_{M}\cdot {\ddot {\psi }}_{M}(t)\cdot \delta \psi _{M}+M_{M}\cdot \left(\psi _{M}+\phi (t)\right)-M_{W}\cdot \delta \psi _{W}\\&=0\end{array}}

.

Since the gearbox is built into the car, the wheel-side relative gear-box-angle is

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\psi}_{W} = \psi_W(t) + \phi(t)}

and on the motor-side

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\psi}_{M} = \psi_M(t) - \phi(t)} .

With the gear transmission ratio

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_G = \frac{\displaystyle \tilde{\psi}_M}{\displaystyle \tilde{\psi}_W}}

and

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{q}_E = \left( \begin{array}{c} \phi(t)\\ \psi_W(t) \end{array} \right)}

we find

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta W = \delta \underline{q}_E \cdot \left( - \underline{\underline{M}}_E \cdot \underline{\ddot{q}}_E + \left( \begin{array}{c} -n_G\cdot M_M\\ +n_G\cdot M_M-M_W\\ \end{array} \right) \right)}

with

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\underline{M}}_E=\begin{pmatrix}\left( {{n}_{G}^{2}}+2 {n_G}+1\right) \, {J_M} & -\left( {{n}_{G}^{2}}+{n_G}\right) \, {J_M}\\ -\left( {{n}_{G}^{2}}+{n_G}\right) \, {J_M} & {{n}_{G}^{2}}\, {J_M}\end{pmatrix}} .

We have thus "returned" all state variables to the Car-Body-submodel.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 16.04.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2021-02-08                            */
/* ref: Modelling and Simulation (TUAS)                */
/* description: virtual work of drive train mechanics  */
/*******************************************************/

/*******************************************************/
/* declarations                                        */
/*******************************************************/
declare("δ", alphabetic);
declare("φ", alphabetic);
declare("ψ", alphabetic);

/*******************************************************/
/* kinematics                                          */
/*******************************************************/
kin : [ψ[M,r] = n[G]*ψ[W,r],
       ψ[W,r] = ψ[W](t) - φ(t),
       ψ[M,r] = ψ[M](t) + φ(t)];
Q : [ψ[M](t),ψ[M,r],ψ[W,r]];
sol: ratsimp(solve(kin,Q))[1];


/* Principle of Virtual Work */
PVW: δW = - J[M]*diff(ψ[M](t),t,2)*δψ[M] + M[M]*(δψ[M]+δφ) - M[W]*δψ[W];

/* minimal coordinates */
q : [ φ(t), ψ[W](t)];
δq: [δφ   ,δψ[W]   ];

varia: [ψ[M](t)=δψ[M],ψ[M,r]=δψ[M,r],ψ[W,r]=δψ[W,r],
        ψ[W](t)=δψ[W], φ(t) =δφ];
sol : expand(append(sol, subst(varia,sol)));

PVW : expand(subst(sol,PVW));
PVW : ev(PVW,nouns);

eom : makelist(coeff(rhs(PVW),δq[i]),i,1,2);
eom : ratsimp(eom);

MM : funmake('matrix,makelist(makelist(ratsimp(coeff(-eom[i],'diff(q[j],t,2))),j,1,2),i,1,2));

rest : expand(eom + makelist(sum(MM[i,j]*diff(q[j],t,2),j,1,2),i,1,2));

print(δq, "*(-",MM,"*",transpose(diff(q,t,2)),"+",transpose(rest),") = 0")$

Consequently, the drive train has only one state-variable: I_M:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{q}_E(t) = \left( I_M(t) \right)}

where

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\displaystyle d}{\displaystyle d t} {I_M}(t)=\frac{\displaystyle {U_B} \operatorname{p}(t)-R\, {I_M}(t)-e}{\displaystyle L}}

and with this algebraic equation

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e = k_e \cdot \underbrace{\left(\dot{\psi}_M(t) + \dot{\phi}(t) \right)}_{\displaystyle =\tilde{\omega}_M = n_G \cdot \tilde{\omega}_W}} .

Keep in mind that Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\omega}_M} and Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\omega}_W} are the rotational velocities of the gearbox-shafts relative to the car-body, thus

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{ll}\tilde{\omega}_W &= \frac{\displaystyle d\,\tilde{\psi}}{\displaystyle d\, t}\\ &= \left( \underbrace{\frac{\displaystyle d\, \psi}{\displaystyle d\, t}}_{\displaystyle =\omega} - \frac{\displaystyle d\, \phi}{\displaystyle d\, t}\right)\end{array}} .

Variables

name	symbol	unit
motor current	I_M	A

Parameter

System parameters for the motor are k_T, k_e and R_M . For the stationary (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\displaystyle d \; I_M}{\displaystyle dt} = 0} ) - condition, we derive

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_M=\frac{{U_M}\, {k_T}-{k_T}\, {k_e} \tilde{\omega}_M }{{R_M}}} ,

so that we see:

under a "no-load"-condition M_M=0, we have
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\omega}_{NL} = \frac{U_M}{k_e}}
under the "stalled motor"-condition Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\omega}_{St}=0} , we have
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{St} = k_T \cdot I_{St}} and Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R = \frac{\displaystyle U_M}{\displaystyle I_{St}}} .

Thus - for U_M = 12 V - we can import measured performance parameters and then replace k_T, k_e, R_M by Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\omega}_{NL}} , I_St and M_St, which make the system parameters to be selected more descriptive.

name	symbol	value	unit
nominal voltage	U_ref	12	V
no-load rotational speed	Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\omega}_{NL}}	14800	rpm
stall-current	I_St	0.25	A
stall-torque	M_St	0.042	N m
inductance	L	0.05	H
gear tramission ratio	n_G	25	1

Back to Start →

References

...

Gelöste Aufgaben/JUMP/E-Motor and Drive-Train

Inhaltsverzeichnis

Scope