Gelöste Aufgaben/FEB2

Aufgabenstellung

Die zwei Euler-Bernoulli-Balken AB (Länge a) und BC (Länge 2a) sind in B fest verschweißt. Ihre Biegesteifigkeit ist EI. Die Konstruktion ist in A fest eingespannt und in C durch ein verschiebliches Gelenklager gelagert. In B ist sie durch die Kraft F und das Moment M belastet.

Lageplan

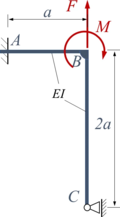
Gesucht ist die Verschiebungen und Verdrehungen der Balken mit der Methode der Finiten ELemente.

Gegeben: a, E I, F, M

Lösung mit Maxima

Berechnet werden sollten daf[r die Auslenkungen und Verdrehung der Punkte A, B und C. Das Modell soll aus zwei Finiten Elementen bestehen, jeweils eins für den Abschnitt AB und BC. Die neutralen Fasern der beiden Balken seien in Längsrichtung undehnbar – die Querschnitts-Schwerpunkte verschieben sich also nicht in Balken-Längsrichtung.

Hier müssen die Element-Steifigkeitsmatrizen für zwei Sektionen von Euler-Bernoulli-Balken zusammengefügt (assembliert) werden. Die Schwierigkeit liegt darin, die Koordinaten in Punkt B passend zu wählen.===Header=== Text

1+1

))tmp)) Die Element-Steifigkeitsmatrix kopieren wir aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken zu:

$\displaystyle K_{i}(\ell _{i})={\frac {EI}{\ell _{i}^{3}}}\cdot {\begin{pmatrix}12&6\cdot \ell &-12&6\cdot \ell _{i}\\6\cdot \ell _{i}&4\cdot {{\ell _{i}}^{2}}&-6\cdot \ell _{i}&2\cdot {{\ell _{i}}^{2}}\\-12&-6\cdot \ell _{i}&12&-6\cdot \ell _{i}\\6\cdot \ell _{i}&2\cdot {{\ell _{i}}^{2}}&-6\cdot \ell _{i}&4\cdot {{\ell _{i}}^{2}}\end{pmatrix}}$.

Die Element-Längen der zwei Finiten Elemente sind hier

${\begin{array}{l}\ell _{1}=a\\\ell _{2}=2\,a\end{array}}$.

Zunächst hat das System mit zwei Finiten Elementen jeweils 4 Koordinaten, nämlich

$W_{i-1},\Phi _{i-1},W_{i},\Phi _{i}$.

Sektino AB

Sektion BC

Die Sektion ist in A fest eingespannt, also ist hier $W_{i-1}=0,\;\Phi _{i-1}=0.$ Es bleiben die Verschiebung und Verdrehung in B, also $W_{i}=W_{B},\;\Phi _{i}=\Phi _{B}$.

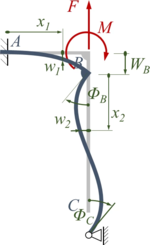
Die neutralen Fasern der Balken-Sektionen - also auch von AB - sind undehnbar. Die Punkte B und C können sich also nur in vertikale Richtung jeweils um WB verschieben.  Durch diese Starrkörper-Verschiebung wird keine Arbeit geleistet - das tun nur die Lateral-Verschiebungen in w2(x2). Es ist also $W_{i-1}=0,\;W_{i}=0.$ Es bleiben also die Verdrehungen in B und C zu $\Phi _{i-1}=\Phi _{B},\;\Phi _{i}=\Phi _{C}$

Übertragung der Koordinaten.

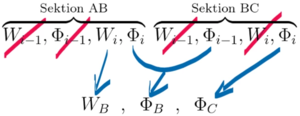
Die verbleibenden Koordinaten des Gesamtsystems sind

${\underline {Q}}=\left({\begin{array}{l}W_{B}\\\Phi _{B}\\\Phi _{C}\end{array}}\right)$

Das verformte System sieht dann so aus:

Verformte Lage.

===Coordinates===

Text

1+1

Wir bauen das Gleichungssystem

${\underline {\underline {K}}}\cdot {\underline {Q}}={\underline {P}}$

zusammen, indem wir die Anteile der Element-Steifigkeitsmatrizen und die äußeren Lasten in die jeweiligen System Matrizen hineinaddieren.

Die virtuelle Formänderungsenergie ist

• für Sektion AB:

$\delta \Pi _{AB}=\left(\delta W_{B},\delta \Phi _{B}\right)\cdot {\begin{pmatrix}\displaystyle {\frac {12\cdot {\mathit {EI}}}{{a}^{3}}}&\displaystyle -{\frac {6\cdot {\mathit {EI}}}{{a}^{2}}}\\\displaystyle -{\frac {6\cdot {\mathit {EI}}}{{a}^{2}}}&\displaystyle {\frac {4\cdot {\mathit {EI}}}{a}}\end{pmatrix}}\cdot \left({\begin{array}{l}W_{B}\\\Phi _{B}\end{array}}\right)$ und

• für Section BC:

$\delta \Pi _{BC}=\left(\delta \Phi _{B},\delta \Phi _{C}\right)\cdot {\begin{pmatrix}\displaystyle {\frac {2\cdot {\mathit {EI}}}{a}}&\displaystyle {\frac {\mathit {EI}}{a}}\\\displaystyle {\frac {\mathit {EI}}{a}}&\displaystyle {\frac {2\cdot {\mathit {EI}}}{a}}\end{pmatrix}}\cdot \left({\begin{array}{l}\Phi _{B}\\\Phi _{C}\end{array}}\right)$

Die Gesamt-Steifigkeitsmatrix aus Sektion AB (rot) und Sektion 2 (grün) ist damit

$\displaystyle {\underline {\underline {K}}}={\frac {E\,I}{a^{3}}}\cdot \left({\begin{array}{ccc}{\color {red}{+12}}&{\color {red}{-6a}}&0\\{\color {red}{-6a}}&{\color {red}{4a^{2}}}+{\color {green}{2a^{2}}}&{\color {green}{a^{2}}}\\0&{\color {green}{a^{2}}}&{\color {green}{2a^{2}}}\end{array}}\right)$,

Die Spaltenmatrix der eingeprägten, äußeren Lasten auf das System kommt aus

$\delta W^{a}=-F\cdot \delta W_{B}+M\cdot \delta \Phi _{B}$

zu

$\displaystyle {\underline {P}}=\left({\begin{array}{r}-F\\M\\0\end{array}}\right)$.===Assembly of System Matrices=== Text

1+1

Die Lösung des linearen Gleichungssystems lievert

${\begin{pmatrix}{{W}_{B}}\\{{\Phi }_{B}}\\{{\Phi }_{C}}\end{pmatrix}}={\begin{pmatrix}{\frac {12\cdot {{a}^{2}}\cdot M-11\cdot {{a}^{3}}\cdot F}{60\cdot {\mathit {EI}}}}\\{\frac {2\cdot a\cdot M-{{a}^{2}}\cdot F}{5\cdot {\mathit {EI}}}}\\-{\frac {2\cdot a\cdot M-{{a}^{2}}\cdot F}{10\cdot {\mathit {EI}}}}\end{pmatrix}}$===Solving=== Text

1+1

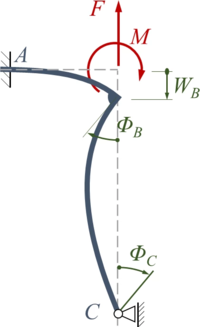
Solange

$\displaystyle M>{\frac {11\cdot a\cdot F}{12}}$

sieht das System im ausgelenkten Zustand so aus:

Lage des verformten Systems.

===Post/Processing===

Text

1+1

Links

• ...

Literature

• ...