Gelöste Aufgaben/DGEB

Aus numpedia
Zur Navigation springen Zur Suche springen

Aufgabenstellung

In dieser Aufgabe starten wir von "first principles" - hier das Prinzip der virtuellen Verrückungen - und entwicklen die Bewegungsgleichunge für einen schlanken Stab unter Langskräft und Biegemoment.

Lageplan.

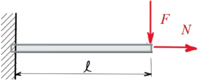
Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab mit Rechteck-Querschnitt unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie δΠ.

Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens.


Lösung mit Maxima

Wie alle zentralen Begriffe der Elastizitätstheorie ineinandergreifen, um die virtuelle Formänderungsenergie für den Euler-Bernoulli-Balken zu ermitteln, zeigt diese Aufgabe.

Header

Hier kommen

zum Einsatz. 


/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2016-03-27                            */
/* ref: Euler-Bernoulli Beam                           */
/* description: derives the equations of motion for    */
/*              the Timoshenko and EBB beam            */
/*******************************************************/




Declarations

Wir brauchen das volle Instrumentarium der Elastizitätstheorie - angefangen bei einfachen Abkürzungen wie der Querschnittsfläche A bis zu den Flächenmomenten 2. Grades Iy und Iz:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{ccc} \displaystyle I_y&=&\frac{b \cdot h^3}{12},\\ \displaystyle I_z&=&\frac{h \cdot b^3}{12},\\ \displaystyle A&=&b\cdot h \end{array}}

über Lame's Konstante

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda=\frac{E \cdot \nu}{\left( 1-2 \cdot \nu \right) \cdot \left( \nu+1 \right) }, \mu=\frac{E}{2 \cdot \left( \nu+1 \right) }} ,

und dem linearen Werkstoffgesetz (|Spannungs-Dehnungs-Beziehung 

/ Hook's Gesetz)
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\underline{E} } = \begin{pmatrix} 2\cdot \mu+\lambda & \lambda & \lambda & 0 & 0 & 0\\ \lambda & 2\cdot \mu+\lambda & \lambda & 0 & 0 & 0\\ \lambda & \lambda & 2\cdot \mu+\lambda & 0 & 0 & 0\\ 0 & 0 & 0 & \mu & 0 & 0\\ 0 & 0 & 0 & 0 & \mu & 0\\ 0 & 0 & 0 & 0 & 0 & \mu\\ \end{pmatrix}} .

Und schließlich wollen wir die |Verzerrungs-Verschiebungs-Beziehung für einen materiellen Punkt P angeben. Grundlage ist die Verschiebung eines Punkte P=[x,y,z] und die gesuchten Koeffizienten u, v, w der Verschiebung in die drei Raumrichtungen

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{r}_P} ,

Die Koeffizienten u(x,y,z), v(x,y,z), w(x,y,z) des Ortsvektors rP beschreiben dabei das Verscheibungsfeld des Balkens. Wir erhalten mit den allgemeinen Komponenten u, v und w des Verschiebungsfeldes

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{r}_P = \left(\begin{array}{l}u(x,y,z)\\v(x,y,z)\\w(x,y,z)\end{array}\right)}

die Verzerrungen allgemein zu

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{ll} {{\varepsilon}_{x,x}}&=\displaystyle \frac{d}{d\,x}\cdot u\left( x,y,z\right) \\ {{\varepsilon}_{y,y}}&=\displaystyle \frac{d}{d\,y}\cdot v\left( x,y,z\right) \\ {{\varepsilon}_{z,z}}&=\displaystyle \frac{d}{d\,z}\cdot w\left( x,y,z\right) \\ {{\varepsilon}_{x,y}}&=\frac{\displaystyle \frac{d}{d\,y}\cdot u\left( x,y,z\right) +\displaystyle \frac{d}{d\,x}\cdot v\left( x,y,z\right) }{\displaystyle 2}\\ {{\varepsilon}_{x,z}}&=\frac{\displaystyle \frac{d}{d\,z}\cdot u\left( x,y,z\right) +\displaystyle \frac{d}{d\,x}\cdot w\left( x,y,z\right) }{\displaystyle 2}\\ {{\varepsilon}_{y,z}}&=\frac{\displaystyle \frac{d}{d\,z}\cdot v\left( x,y,z\right) +\displaystyle \frac{d}{d\,y}\cdot w\left( x,y,z\right) }{\displaystyle 2} \end{array}} .

Damit das "schöner" aussieht,, kürzen wir im Folgenden ab

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \displaystyle \frac{d}{dx}(.) := (.)_x, \;\;\frac{d}{dy}(.) := (.)_y, \;\;\frac{d}{dz}(.) := (.)_z, }

und erhalten als |Verzerrungs-Verschiebungs-Beziehung

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{ll} {{\varepsilon}_{x,x}}&= u_x \\ {{\varepsilon}_{y,y}}&= v_y \\ {{\varepsilon}_{z,z}}&= w_z \\ {{\varepsilon}_{x,y}}&= \frac{\displaystyle 1}{\displaystyle 2}\left(u_y+v_x \right)\\ {{\varepsilon}_{x,z}}&= \frac{\displaystyle 1}{\displaystyle 2}\left(u_z+w_x \right)\\ {{\varepsilon}_{y,z}}&= \frac{\displaystyle 1}{\displaystyle 2}\left(v_z+w_y \right)\\ \end{array} } .

Für unser Problem suchen wir jetzt ein konkretes Verschiebungsfeld, das unseren Anforderungen an das Problem genügt. 


/*******************************************************/
/* declare variational variables */
declare("δW", alphabetic); /* virtual work */
declare("δA", alphabetic); /* virtual work of implied external forces */
declare("δΠ", alphabetic); /* virtual strain energy */
declare("δu", alphabetic); /* variation of u */
declare("δw", alphabetic);
declare("δφ", alphabetic);
declare("δη", alphabetic);
declare("δθ", alphabetic);
declare("λ" , alphabetic); /* otherwise, this is the lambda fct. */
declare("μ" , alphabetic);
declare("Δr", alphabetic); /*displacement of material point [x,y,z] */
declare("δΔr",alphabetic); /* variation of Δr */
declare("δZ", alphabetic); /* variation of strain */

/*******************************************************/
/* parameters */
/* abbreviate: */
geometry  : [h^3 = 12*I[y]/b, b^3 = 12*I[z]/h, b = A/h];
/* Lame's Constants                                */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
lameConst : [λ = e*nu/((1+nu)*(1-2*nu)), μ = e/(2*(1+nu))];

/* relation: hook's law, modulus of elasticity     */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
E :  matrix([2*μ+λ,     λ,     λ,  0,  0,  0],
            [    λ, 2*μ+λ,     λ,  0,  0,  0],
            [    λ,     λ, 2*μ+λ,  0,  0,  0],
            [    0,     0,     0,  μ,  0,  0],
            [    0,     0,     0,  0,  μ,  0],
            [    0,     0,     0,  0,  0,  μ]);

/* Strain Displacement Relation */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
StrainDispl(arg) := [epsilon[x,x] =      diff(arg[1],x),
                     epsilon[y,y] =      diff(arg[2],y),
                     epsilon[z,z] =      diff(arg[3],z),
                     epsilon[x,y] = 1/2*(diff(arg[1],y) + diff(arg[2],x)),
                     epsilon[x,z] = 1/2*(diff(arg[1],z) + diff(arg[3],x)),
                     epsilon[y,z] = 1/2*(diff(arg[2],z) + diff(arg[3],y))];




Euler Rotation

Wir definieren später ein Modell, bei dem Querschnitte um eine Achse senkrecht zur Papierebene kippen kann. Das beschreiben wir mit der linearisierten Euler-Rotation:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{D}_{2}}\left( \mathit{arg}\right) =\begin{pmatrix}1 & 0 & -\mathit{arg}\\ 0 & 1 & 0\\ \mathit{arg} & 0 & 1\end{pmatrix}} ,

die für arg << 1 gilt. 


/*******************************************************/
/* kinematics: Euler-rotation about y-Axis */
D[2](arg) := [[  1   ,   0  ,-arg ],
              [  0   ,   1  ,  0  ],
              [+arg  ,   0  ,  1  ]];




Stress-Strain-Relations for a Rod

Die Komponenten des Spannungs- und Verzerrungs-Tensors fassen in den Matrizen

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\sigma} = \begin{pmatrix}{{\sigma}_{x,x}}\\ {{\sigma}_{y,y}}\\ {{\sigma}_{z,z}}\\ {{\sigma}_{y,z}}\\ {{\sigma}_{x,z}}\\ {{\sigma}_{x,y}}\end{pmatrix}}

und

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\varepsilon} =\begin{pmatrix}{{\varepsilon}_{x,x}}\\ {{\varepsilon}_{y,y}}\\ {{\varepsilon}_{z,z}}\\ {{\varepsilon}_{y,z}}\\ {{\varepsilon}_{x,z}}\\ {{\varepsilon}_{x,y}}\end{pmatrix}}

zusammen - und damit können wir nun anfangen zu arbeiten.

Die wichtigsten Annahmen zu Spannungen in einem einfachen Stab mit symmetrischen Profil sind:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{pmatrix}{{\sigma}_{y,y}}=0\\ {{\sigma}_{z,z}}=0\\ {{\sigma}_{y,z}}=0\\ {{\sigma}_{x,y}}=0\end{pmatrix}}

Die ersten beiden Zeilen sind klar: die Hauptspannungen senkrecht zur Stab-Längsachse verschwinden. Ausnahmen machen hier nur Stäbe, die z.B. durch großen Drücke belastet sind wie bei Bohrsträngen.

Scherung - nicht betrachtet.


Die Zeilen 3 und 4 gehören zu Spannungen, die einen Querschnitt in der skizzierten Weise verformen (schweren) würden. Das passiert bei symmetrischen Querschnitten wie hier einem Rechteck-Querschnitt nicht.

Mit diesen vier Annahmen können wir aus der Beziehung

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\sigma} = \underline{\underline {E}}\cdot\underline{\varepsilon}}

vier Gleichungen herausnehmen und wählen

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{ll}{{\varepsilon}_{x,y}}&=0\\ {{\varepsilon}_{y,z}}&=0\\ {{\varepsilon}_{y,y}}&=\displaystyle -\frac{{{\varepsilon}_{x,x}}\cdot \lambda}{2\cdot \mu+2\cdot \lambda}\\ {{\varepsilon}_{z,z}}&=\displaystyle -\frac{{{\varepsilon}_{x,x}}\cdot \lambda}{2\cdot \mu+2\cdot \lambda}\end{array}} .

/*******************************************************/
/* definitions: components of stress / strain tensors */
Sigma   : matrix([sigma[x,x]], [sigma[y,y]], [sigma[z,z]], 
                 [sigma[y,z]], [sigma[x,z]], [sigma[x,y]]);
Epsilon : matrix([epsilon[x,x]], [epsilon[y,y]], [epsilon[z,z]],
                 [epsilon[y,z]], [epsilon[x,z]], [epsilon[x,y]]);

/* Stress Strain Relation */
StressStrain : solve(args(transpose(Sigma - E.Epsilon)[1]),args(transpose(Sigma)[1]))[1];

/* assumptions for stresses: */
assumptions : [sigma[y,y]=0,sigma[z,z]=0,sigma[y,z]=0, sigma[x,y]=0];

/* this implies for the strains: */
consequence : solve(subst(StressStrain, assumptions),
                       [epsilon[x,y],epsilon[y,z],epsilon[y,y],epsilon[z,z]])[1];




Displacement Variables

Wir starten, indem wir die Koordinaten der Verschiebung aller Punkte auf dem Querschnitt festlegen:


Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u(x)} ...Auslenkung des Punktes (x,0,0) in Stab-Längsrichtung 'x',
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w(x)} ...Auslenkung des Punktes '(x,0,0)' in 'z'-Richtung,
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi(x)} ...Drehung des Querschnitts 'x' um die 'y'-Achse,
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta(y,z)} ...eine Funktion, die die Verschiebung der materiellen Punkte des Querschnitts in 'y'-Richtung erfasst,
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta(y,z)} ...eine Funktion, die die Verschiebung der materiellen Punkte des Querschnitts in 'z'-Richtung erfasst

und mit diesen die Komponenten des Verschiebungsvektors

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta\underline{r}=\left(\begin{array}{c} u -\phi \cdot z\\ \eta(y,z) \\ w+ \theta(y,z) \end{array}\right)} .

Für die verformte Struktur können wir die Koordinaten in eine Skizze eintragen, um sie besser zu verstehen:

Koordinaten u, w.
Koordinate ϕ

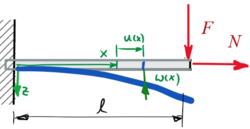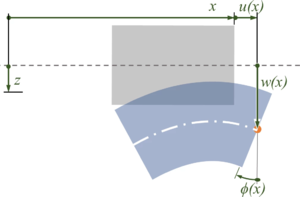Besonders die Verschiebung in "x"-Richtung z∙ϕ durch eine Kippung des Querschnitts schauen wir uns genauer an:

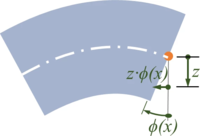
Verscheibung eines materiellen Punktes in x-Richtung.

Analog gehen wir für die Variation des Verschiebungsvektors und seiner Koordinaten vor. 


/*******************************************************/
/* coordinates of cross-section displacement and their variations */
coords : [[ u(x), w(x),phi(x),eta(y,z),theta(y,z)],
          [δu(x),δw(x), δφ(x), δη(y,z),   δθ(y,z)]];

/* coordintes od displancemnt (d) for any material point */
d: Δr  = expand([x+u(x),0,w(x)] + [0,y+eta(y,z),z+theta(y,z)].D[2](-phi(x))) - [x,y,z];
/* linearize wrt. theta, phi << 1 */
d: subst(0,phi(x)*theta(y,z),d);

/*  and variation of Δr */
d: [d, δΔr = sum(subst(0,kappa,diff(
                         subst(coords[1][i]+kappa*coords[2][i],coords[1][i],subst(d,Δr))
                                                                 ,kappa)),i,1,length(coords[1]))];




Virtual Strain Energy

Jetzt haben wir alles parat, um die Virtuelle Formänderungsenergie hinzuschreiben, nämlich die Spannungen

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\sigma}=\begin{pmatrix}\displaystyle \lambda\cdot \left( u_x(x) -\phi_x(x) \cdot z-\frac{2\cdot \left( u_x(x) -\phi_x(x)\cdot z\right) \cdot \lambda}{2\cdot \mu+2\cdot \lambda}\right) +2\cdot \left( u_x(x) -\phi_x(x) \cdot z\right) \cdot \mu\\ 0\\ 0\\ 0\\ \displaystyle \frac{\left( \displaystyle w_x(x) -\phi\left( x\right) \right) \cdot \mu}{2}\\ 0\end{pmatrix}}

und die Variation der Dehnung, nämlich

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta\underline{\epsilon} = \begin{pmatrix}\displaystyle \delta u_x(x) -\delta \phi_x(x) \cdot z\\ \displaystyle -\frac{\left( \delta u_x(x) -\delta \phi_x(x) \cdot z\right) \cdot \lambda}{2\cdot \mu+2\cdot \lambda}\\ \displaystyle -\frac{\left( \delta u_x(x) -\delta \phi_x(x) \cdot z\right) \cdot \lambda}{2\cdot \mu+2\cdot \lambda}\\ 0\\ \displaystyle \frac{\delta w_x(x) -\delta \phi(x)\left( x\right) }{2}\\ 0\end{pmatrix}}

Damit setzen wir an

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta\Pi = \displaystyle \int_A \underline{\sigma} \cdot \delta \underline{\epsilon}\;dA}

Der Ausdruck für die virtuelle Formänderungsenergie ist noch etwas sperrig, aber das gibt sich gleich, wenn wir die Integration über den Querschnitt A ausführen und

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A = b\cdot h, \;\;I_y = \displaystyle \frac{b\cdot h^3}{12}}

setzen. 


/*******************************************************/
/* stresses and strains under assumptions made and displacement-coordinates given */
stress : S = subst(StrainDispl(
                        subst(d[1],Δr)),subst(consequence,
                                   subst(StressStrain,subst(assumptions,Sigma))));
strain :δZ = subst(StrainDispl(subst(d[2],δΔr)),subst(consequence,Epsilon));

/* virtual strain energy */
VSE : δΠ = integrate(integrate(expand(
                     subst(strain, subst(stress,
                                        S.δZ
                                            ))
                                     ), y,-b/2,b/2),z,-h/2,h/2);
/* simplify */
VSE : ratsimp(expand(subst(lameConst,subst(geometry, expand(VSE)))));




Timoshenko-Beam

Dann erhalten wir - sortiert nach den den Bewegungsgleichungen (Feld-Differentialgleichungen) für u, w und ϕ:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rc}\delta\Pi =& E\;A \;\;\; u_x \cdot \delta u_x\\+& \displaystyle \frac{1}{4} G\;A \; \left(w_x-\phi \right) \cdot \delta w_x \\+&\displaystyle \frac{1}{4} G\;A\;\left(\phi-w_x\right)\cdot\delta\phi + E\;I_y\;\phi_x \cdot\delta \phi_x \end{array}} .

Hier treten Ableitungen nur noch nach der Koordinate x auf, wir können die Bewegungsgleichungen nun in gewohnter Form mit

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \displaystyle \frac{d(.)}{dx} = (.)_x =: (.)'}

als

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{c}E\;A \; u' \cdot \delta u' = 0 \\ \displaystyle \frac{1}{4} G\;A \; \left(w'-\phi \right) \cdot \delta w' = 0\\ \displaystyle \frac{1}{4} G\;A\;\left(\phi-w'\right)\cdot\delta\phi + E\;I_y\;\phi' \cdot\delta \phi'=0 \end{array}}

schreiben. 


/*******************************************************/
/* first result: general equations of motion incl. Timoshenko-Beam and tension rod */

collect : [ δu(x), δw(x), δφ(x)]$
collect: append(collect,diff(collect,x));

take: expand(subst(VSE, δΠ));
tmb : ratsimp(makelist(
  coeff(take,collect[i])*collect[i] + coeff(take,collect[i+3])*collect[i+3]=0,
                        i,1,3));
sub : alpha=8*nu+8;
tmb : expand(subst(sub,expand(subst(solve(sub,nu),tmb))));

shearModulus: [G = e/(2*(1+nu))];
tmb : expand(subst(solve(shearModulus,nu),tmb));




Euler-Bernoulli-Balken

Noch einfacher wird es mit dem Ansatz von Euler-Bernoulli, die mit der zusätzlichen Vereinfachung

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \displaystyle \phi (x) = \frac{d w(x)}{d x}\;\;\;} bzw.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \displaystyle \delta \phi (x) = \frac{d\; \delta w(x)}{d x}}

auf

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{c} E\;A \; u' \cdot \delta u'=0\\ E\;I_y\; w'' \cdot \delta w''=0\end{array}}

führt. 


/*******************************************************/
/* further simplify to Euler - Bernoulli-Hypothesis
   (cross sections to remain perpendicular to neutral fiber (axis)) */
EBhypothesis : [phi(x)=-diff( w(x),x),
                 δφ(x)=-diff(δw(x),x)];

ebb : expand(subst(EBhypothesis,tmb));
ebb : ev(ebb,nouns);
ebb : expand(subst(sub,expand(subst(solve(sub,nu),ebb))));
ebb : [ebb[1],subst(ebb[2],ebb[3])];





Links

Literature

  • ...
Abgerufen von „https://numpedia.rzbt.haw-hamburg.de/index.php?title=Gelöste_Aufgaben/DGEB&oldid=1060“