Gelöste Aufgaben/Kitb
Aufgabenstellung
Diese Aufgabe ist eine Variante der Aufgabe „Kita“, bei der die analytische Lösung gesucht ist.
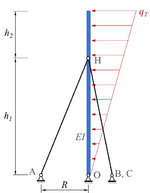
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird.
Gesucht ist die Näherungslösung für ein FE-Modell des Masts (Euler-Bernoulli-Balken) und der drei Dehnstäbe.
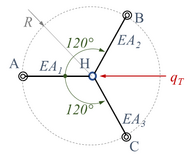
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „O“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „H“ mit dem Mast verbunden und in den Punkten „A“, „B“ und „C“ gelenkig gelagert. Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert qT und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt h1 = 2 h2, h2 = √2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A2=2 E A1,E A3=E A1.
Der Mast hat ein zylindrisches Profil mit Innen- und Außendurchmesser di, da.
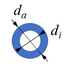
Ein Knicken der drei Stäbe sei ausgeschlossen.
Lösung mit Maxima
Mit Maxima berechnen wir die Lösung des Problems mit der Methode der Finiten Elemente. Da wir in Aufgabe „Kita“ bereits die Knoten-Variablen als Hilfsgrößen eingeführt haben, können wir die Nomenklatur, Parameter und abgeleitete Größen direkt übernehmen - und die Ergebnisse auch vergleichen.
Header
Kern der Lösung ist die Komposition der Element-Steifigkeitsmatrix sowie der "rechten Seite" des Gleichungssystems.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 21.05.2 */
/* author: Andreas Baumgart */
/* last updated: 2022-08-19 */
/* ref: NMM, Labor 2 */
/* Mast unter linear-veränderlicher Windlast */
/* - Lösung mit der Methode der FE */
/*******************************************************/
Declarations
Die Parameter können wir direkt aus Kita übernehmen. Hinzu kommt die Definition der Trial-Functions aus FEM-Formulierung für den Euler-Bernoulli-Balken – die wir anstelle der allgemeinen Lösung der Differentialbeziehung für w(x), v(x) ansetzen:
/*******************************************************/
/* declarations */
/* *****************************************************/
/* parameter selection */
params: [[EA[2]=2*EA[1],EA[3]=EA[1], EA[1] = α*EI/R^2], [h[1] = 2*h[2], h[2]=sqrt(2)*R]];
assume(R>0);
/* trial-functions */
φ : [ 2*ξ^3-3*ξ^2+1,
(ξ^3-2*ξ^2+ξ)*ℓ[i],
3*ξ^2-2*ξ^3,
(ξ^3-ξ^2)*ℓ[i]];
/* non-sclar variables */
declare(r,nonscalar,
e,nonscalar);
/* geometry **********************************/
/* points */
geo: [r[H] = matrix([ h[1], 0, 0]),
r[A] = matrix([ 0 , R*sin( 0 ),-R*cos( 0 )]),
r[B] = matrix([ 0 , R*sin(-2*%pi/3),-R*cos(-2*%pi/3)]),
r[C] = matrix([ 0 , R*sin(+2*%pi/3),-R*cos(+2*%pi/3)])];
geo: append(geo, subst(geo, [r[1] = r[A]-r[H],
r[2] = r[B]-r[H],
r[3] = r[C]-r[H]]));
geo: append(geo, [L = sqrt(subst(geo,r[1]).subst(geo,r[1]))]);
/* unit-vecotor coefficients */
geo: append(geo, makelist(e[i]=subst(geo,r[i]/L),i,1,3));
Wir verwenden außerdem die Abkürzung .
Kinematics
Die Koordinaten der drei beweglichen Knoten O, H und T definieren die Kinematik des Systems. Wie in Kita sind dies die Verschiebungen und Verdrehungen der Knoten-Querschnitte in H und T in die zwei Raumrichtungen z und y, also
- ,
sowie die Verdrehung des Querschnitts in „O“ mit den Kippwinkeln, also
- .
Diese System-Variablen fassen wir elementweise zusammen, z.B. für wi(x) als
Die Verschiebung der Querschnitte eines FE-Elements können wir dann – hier am Beispiel von wi(x) – über die Funktion
darstellen, wobei für die Elementlänge hier
gilt. Alle Knotenvariablen des Systems fassen wir nun unter
zusammen, die Variation der Knotenvariablen entsprechend unter
/**********************************************************/
/* kinematics */
/* ********************************************************/
/* coordinates */
δQ : [δΦ[O],δW[H],δΦ[H],δW[T],δΦ[T],δΨ[O],δV[H],δΨ[H],δV[T],δΨ[T]];
Q : [ Φ[O], W[H], Φ[H], W[T], Φ[T], Ψ[O], V[H], Ψ[H], V[T], Ψ[T]];
Equlibrium Condition
Die Gleichgewichtsbedingungen nach dem Prinzip_der_virtuellen_Verrückungen sind
Für die Implementierung in ein Rechnerprogramm formulieren wir dabei
und komponieren die Gesamtsteifigkeitsmatrix aus den Anteilen der virtuellen Formänderungsarbeit und der virtuellen Arbeit der äußeren Last zusammen.
Virtuelle Formänderungsenergie des Masts
Diese Anteile können wir direkt aus der Anleitungen „FEM-Formulierung für den Euler-Bernoulli-Balken“ übernehmen. Wir haben zwei Elemente (von O nach H und von H nach T) und schreiben entsprechend
- .
Die liefern dann den Anteil des Masts an der virtuellen Arbeit, den wir in der Form
anschreiben können
Da der untere Knoten keine Verschiebungs-Freiheitsgrade hat, streichen wir die entsprechenden Zeilen und Spalten der Element-Steifigkeitsmatrix aus FEM:_Trial-Functions für kubische Ansatz-Polynome, der Beitrag des Masts zur Gesamtsteifigkeitsmatrix ist dann
Man sieht in der Matrix sehr schön, wie die Anteile in die beiden Raumrichtungen z und y in der Matrix getrennt sind. Die z-Richtung bevölkert den oberen, linken Teil, die y-Richtung den unteren, rechten Teil. Die Auslenkungen in diese beiden Richtungen sind durch die Steifigkeitsmatrix nicht gekoppelt. Das wird sich ändern, wenn wie die Stäbe mit einbauen.
Virtuelle Formänderungsenergie der Stäbe
Die virtuelle Formmänderungsarbeit des Stabes können wir direkt aus der Stabkraft Si anschreiben, die wir in Kita schon hergeleitet haben. So gilt für
mit
Dabei ist
die virtuelle Verrückung des Kraftangriffspunktes.
Einsetzen liefert dann die Anteile der Stäbe an der virtuellen Arbeit, den wir wieder in der Form
formulieren, ausgeschreiben ist dann
Hier habe wir die Elemente nach den Stäben eingefärbt. Man sieht gut, wie der Term zu einer Kopplung der Auslenkungen in die beiden Raumrichtungen führt, wenn .
Die Gesamtsteifigkeitsmatrix ist nun
Virtuelle Arbeit der Windlast
Die rechte Seite des linearen Gleichungssystems
kommt aus der virtuellen Arbeit der Streckenlast q(x), also
Die stückweise definierte Funktion kennen wir schon aus diesem Abschnitt der Lösung zu "Kita". Für die Integration können wir die auch die Lösung der Faltungsintegrale für die rechte Seite des Gleichungssystems aus äußeren, einprägten Lasten nutzen.
Aber Achtung: die Streckenlast mit unseren Koordinaten ist negativ! Wir erhalten
- .
Die ersten 5 Elemente, die zur z-Richtung gehören - sind ungleich Null, die letzten 5 Element sind gleich Null - so wie erwartet.
/**********************************************************/
/* virtual Work of EBB: δW[t] : δW[q] -δW[Mast] - δW[Rod] */
/* ********************************************************/
declarations: δW[EBB] = EI/ℓ[i]^3*matrix([δW[i-1],δΦ[i-1],δW[i],δΦ[i]]).matrix([ 12 , 6*ℓ[i] ,- 12 , 6*ℓ[i] ],
[6*ℓ[i], 4*ℓ[i]^2,-6*ℓ[i], 2*ℓ[i]^2],
[- 12 ,- 6*ℓ[i] , 12 ,-6*ℓ[i] ],
[6*ℓ[i], 2*ℓ[i]^2,-6*ℓ[i], 4*ℓ[i]^2]).matrix([W[i-1]],[Φ[i-1]],[W[i]],[Φ[i]]);
sectionReplace: [[[ℓ[i]=h[ 1],δW[i-1]= 0 ,δΦ[i-1]=δΦ[O],δW[i]=δW[H],δΦ[i]=δΦ[H], W[i-1]= 0 , Φ[i-1]= Φ[O], W[i]= W[H], Φ[i]= Φ[H]],
[ℓ[i]=h[ 2],δW[i-1]=δW[H],δΦ[i-1]=δΦ[H],δW[i]=δW[T],δΦ[i]=δΦ[T], W[i-1]= W[H], Φ[i-1]= Φ[H], W[i]= W[T], Φ[i]= Φ[T]]],
[[ℓ[i]=h[ 1],δW[i-1]= 0 ,δΦ[i-1]=δΨ[O],δW[i]=δV[H],δΦ[i]=δΨ[H], W[i-1]= 0 , Φ[i-1]= Ψ[O], W[i]= V[H], Φ[i]= Ψ[H]],
[ℓ[i]=h[ 2],δW[i-1]=δV[H],δΦ[i-1]=δΨ[H],δW[i]=δV[T],δΦ[i]=δΨ[T], W[i-1]= V[H], Φ[i-1]= Ψ[H], W[i]= V[T], Φ[i]= Ψ[T]]]];
δW[Mast]: sum(sum(subst(sectionReplace[dir][sec],subst(declarations,δW[EBB])),sec,1,2),dir,1,2);
/* S[i] as a function of W[H] and V[H] *****************/
ΔL: subst(geo,[r[A] - (r[H]+matrix([0,V[H],W[H]])),
r[B] - (r[H]+matrix([0,V[H],W[H]])),
r[C] - (r[H]+matrix([0,V[H],W[H]]))]);
ΔL: makelist(sqrt(ΔL[i].ΔL[i])-subst(geo,L),i,1,3);
displ: [W[H],V[H]];
null : makelist(displ[i]=0,i,1,2);
/* linearize .... */
ΔL: sum(subst(null, diff(ΔL,displ[j]))*displ[j],j,1,2);
S : -makelist(EA[i]*ΔL[i]/subst(geo,L),i,1,3);
δW[Rod]: subst(geo,sum(S[i]*e[i].matrix([0,δV[H],δW[H]]),i,1,3));
/* virtual Work of q(x) *****************/
lineLoad: [q(x) = -(q[i-1]*(1-x/h[i])+q[i]*x/h[i]), [[q[i-1]=0,q[i]=q[H],h[i]=h[1]],[q[i-1]=q[H],q[i]=q[T],h[i]=h[2]]],q[H] = q[T]*h[1]/(h[1]+h[2])];
virtDisp: subst(ℓ[i]=h[i],(δw(x)=[δW[i-1],δΦ[i-1],δW[i],δΦ[i]].φ));
δW[q]: subst(lineLoad[3],sum(subst(sectionReplace[1][sec],subst(lineLoad[2][sec],integrate(subst(ξ=x/h[i],subst(virtDisp,subst(lineLoad[1],q(x)*δw(x)))),x,0,h[i]))),sec,1,2));
/* total virtual Work *****************/
δW[t] : δW[q] -δW[Mast] - δW[Rod];
δW[t]: expand(δW[t])$
equs: makelist(0,i,1,length(Q));
K: zeromatrix(length(Q),length(Q));
p: zeromatrix(length(Q),1);
for row:1 thru length(Q) do
(equs[row]:-coeff(δW[t],δQ[row]),
for col:1 thru length(Q) do
K[row,col]:-coeff(coeff(δW[t],δQ[row]),Q[col]))$
rightHandSide: expand(δW[t]+δQ.K.Q);
for row:1 thru length(Q) do
p[row,1]:coeff(rightHandSide,δQ[row])$
print(ratsimp(subst(params[2],K)),"*",transpose(Q),"=",ratsimp(subst(params[2],p)))$
Solving
Die Lösung des linearen Gleichungssystems liefert das Ergebnis für die Knotenvariablen in :
Für Knotenvariablen wie z.B. kann man zeigen, dass die Ergebnisse identisch sind - auch wenn man im Fall von ein bisschen umformen muss \ldots.
/*******************************************************/
/* solving */
/* *****************************************************/
C: solve(subst(params[1],subst(params[2],equs)), Q)[1];
sol: [[w(x)= [0, Φ[O], W[H], Φ[H]].φ,w(x)= [W[H], Φ[H], W[T], Φ[T]].φ],
[v(x)= [0, Ψ[O], V[H], Ψ[H]].φ,v(x)= [V[H], Ψ[H], V[T], Ψ[T]].φ]];
for dir:1 thru 2 do
for sec:1 thru 2 do
sol[dir][sec]: subst([ℓ[i]=h[sec]],sol[dir][sec]);
sol: subst(α=500,subst(params[1],subst(params[2],subst(C,sol))));
Post-Processing
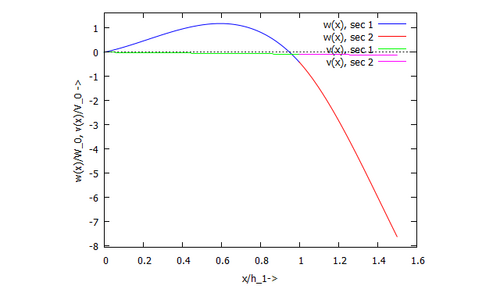
Einsetzten der Knotenvaraiblen in die Ansatzfunktionen liefert dern Verlauf der Auslenkung und Schnittkräfte - hier am Beispiel des Biegemoments: Auch wenn der Verlauf der Auslenkungen identisch zu sein scheint mit der Lösung aus Kita, so sieht man an der zweiten Ableitung - dem Momentenverlauf - doch deutlich, dass das nicht stimmt. Wir sehen also hier eine Näherungslösung für die analytische Rechnung.
 | 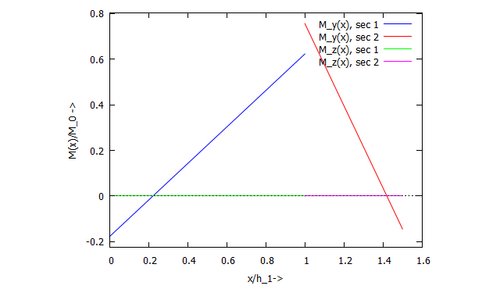 |
/*******************************************************/
/* post-processing */
/*******************************************************/
/* what size is α ? */
/* geopar: [A[1]= π/ 4*d[r]^2, d[r]=1*cm,
I = π/64*(d[o]^4-d[i]^4), d[o]=10*cm, d[i]=9*cm,
R = h[2]/sqrt(2), h[2]=500*cm,
α = A[1]*R^2/I ] */
toPlot: ratsimp([subst(sol[1][1],w(x)/R),subst(sol[1][2],w(x)/R),subst(sol[2][1],v(x)/R),subst(sol[2][2],v(x)/R)]/(q[T]*R^3/6/EI));
plot2d([[parametric, ξ, toPlot[1], [ξ,0,1]],
[parametric, 1+ξ*subst(params[2],h[2]/h[1]), toPlot[2], [ξ,0,1]],
[parametric, ξ, toPlot[3], [ξ,0,1]],
[parametric, 1+ξ*subst(params[2],h[2]/h[1]), toPlot[4], [ξ,0,1]]],
[legend, "w(x), sec 1", "w(x), sec 2", "v(x), sec 1", "v(x), sec 2"],
[xlabel, "x/h_1->"],[ylabel, "w(x)/W_0, v(x)/V_0 ->"])$
toPlot: ratsimp(subst(params[2],[diff(subst(sol[1][1],-EI*w(x)),ξ,2)/h[1]^2,diff(subst(sol[1][2],-EI*w(x)),ξ,2)/h[2]^2,diff(subst(sol[2][1],-EI*v(x)),ξ,2)/h[1]^2,diff(subst(sol[2][2],-EI*v(x)),ξ,2)/h[1]^2]/(q[T]*R^2)));
plot2d([[parametric, ξ, toPlot[1], [ξ,0,1]],
[parametric, 1+ξ*subst(params[2],h[2]/h[1]), toPlot[2], [ξ,0,1]],
[parametric, ξ, toPlot[3], [ξ,0,1]],
[parametric, 1+ξ*subst(params[2],h[2]/h[1]), toPlot[4], [ξ,0,1]]],
[legend, "M_y(x), sec 1", "M_y(x), sec 2", "M_z(x), sec 1", "M_z(x), sec 2"],
[xlabel, "x/h_1->"],[ylabel, "M(x)/M_0 ->"])$
Links
- ...
Literature
- ...