Gelöste Aufgaben/GYRQ

Aufgabenstellung

Die Bewegung eines Kreisels kann man auch anderes als in Aufgabe GYRO mit Euler-Drehwinkeln abbilden, die nicht immer leicht zu interpretieren sind. Natürlich könnten wir dafür in der Ergebnisdarstellung die Euler-Winkel z.B. in Quaternionen umrechnen. Aber hier wollen wir ausprobieren, wie die Bewegungsgleichungen selbst in anderen Koordinaten (vgl. Drehgruppe) aussehen. Und ob wir dadurch numerische Vorteile erwarten können.

Alles andere ist so wie in GYRO.

Kreisel mit gelenkiger Fußpunktlagerung.

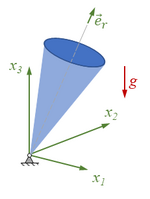
Gesucht ist die Präzessions-Bahn eines Kreisels mit Quaternionen / Kugelkoordinanten. Unser Kreisel ist ein Kegel der Höhe H und Radius R. Die Bewegungsgleichungen sollen mit dem Prinzip der virtuellen Verrückungen aufgestellt werden. Wir suchen nach der Trajektorie des Mittelpunktes des Kreisels für große Kippwinkel.

Lösung mit Maxima und Matlab^®

Wir arbeiten mit Maxima und Matlab.

Maxima brauchen wir zum Aufstellen der Bewegungsgleichungen, die zunächst mal recht komplex aussehen. Dabei nehmen wir die Bewegungsgleichungen wie sie aus den Gleichgewichtsbedingungen kommen und lösen sie als Anfangswertproblem.

Geomertrie des Kreisels

Header

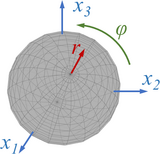
Für die Beschreibung von Drehungen werden oft Quaternionen genutzt. Dabei wird eine Drehung durch die neue Lage der x₃-Achse sowie eine Drehung um diese Achse beschreiben. Für die Ermittlung von Bewegungsgleichungen - z.B. eines Kreisels - eignen sich Quaternionen aber nicht gut: für die Abbildung muss man dafür sorgen, dass die Euler-Achse ein Einheits-Vektor ist.

Euler-Kippwinkel φ₁, φ₂

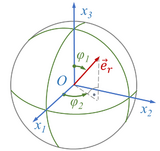
Mit einer kleinen Änderungen können wir diese Idee trotzdem weiter verfolgen. Wir nutzen Kugelkoordinaten, um ein Kippen um die Winkel φ₁, φ₂ zu erfassen, genau wie bei der Beschreibung von Länge- und Breitengraden auf der Erde.

Die Transformationsmatrix zu diesem Ansatz ist

${\underline {\underline {D}}}_{12}\left(\varphi _{1}(t),\varphi _{2}(t)\right)={\begin{pmatrix}\cos {\left({{\varphi }_{1}}(t)\right)}\cos {\left({{\varphi }_{2}}(t)\right)}&\cos {\left({{\varphi }_{1}}(t)\right)}\sin {\left({{\varphi }_{2}}(t)\right)}&-\sin {\left({{\varphi }_{1}}(t)\right)}\\-\sin {\left({{\varphi }_{2}}(t)\right)}&\cos {\left({{\varphi }_{2}}(t)\right)}&0\\\sin {\left({{\varphi }_{1}}(t)\right)}\cos {\left({{\varphi }_{2}}(t)\right)}&\sin {\left({{\varphi }_{1}}(t)\right)}\sin {\left({{\varphi }_{2}}(t)\right)}&\cos {\left({{\varphi }_{1}}(t)\right)}\end{pmatrix}}$

Mit einer weiteren Drehung φ₃ um die Rotationsachse lösen also auch hier das Anfangswertproblem mit den nichtlinearen Bewegungsgleichungen zu den Koordinaten

${\underline {\varphi }}=\left({\begin{array}{c}\varphi _{1}(t)\\\varphi _{2}(t)\\\varphi _{3}(t)\end{array}}\right)$,

Dabei sind die Kippwinkel φ₁, φ₂ nicht mehr die Winkel aus den Euler'schen Drehmatrizen für sukzessive Drehungen bezüglich der x₁- und x₂-Achsen sind, sondern die Winkel von Kugelkoordinaten.

Wie zuvor kommen nun die Gleichgewichtsbedingungen aus dem Prinzip der virtuellen Verrückungen.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 21.05.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2022-04-01                            */
/* ref: gyroscopic precession                          */
/* description: solve using principle of virt. work    */
/*******************************************************/

Declarations

Wir brauchen zunächst die Transformationsmatrizen aus ${\underline {\underline {D}}}_{12}\left(\varphi _{1},\varphi _{2}\right)$ sowie die bekannten Transformationsmatrizen der Euler-Rotation, also die Drehmatrizen, die unser inertiales Koordinatensystem in das Kreiselfeste Koordinatensystem überführt. Wir kippen also zunächst um die x₁ und x'₃-Achse und schließlich um die resultierende Rotationsachse x'₃. Die Koordinatentransformation ist dann

${\underline {\underline {D}}}_{0\to K}={\underline {\underline {D}}}_{3}(\varphi _{3}(t))\cdot {\underline {\underline {D}}}_{12}(\varphi _{1}(t)),\varphi _{2}(t))$.

Und wir führen wiederum die folgenden Abkürzungen für die Systemparameter

${I_{y}}={\frac {\displaystyle 3\left({{R}^{2}}+4{{H}^{2}}\right)m}{20}},{I_{z}}={\frac {\displaystyle 3{{R}^{2}}m}{10}},m={\frac {\displaystyle {\pi }H{{R}^{2}}\rho }{3}}$

und die Zustandsgrößen

${\frac {d}{dt}}{{\varphi }_{i}}(t)={{\omega }_{i}}(t)$

ein.

/*Declarations                                         */
/* Euler-Drehmatrizen */
D[1](φ) := matrix([1,0,0],[0,cos(φ),sin(φ)],[0,-sin(φ),cos(φ)]);
D[2](φ) := matrix([cos(φ),0,-sin(φ)],[0,1,0],[sin(φ),0,cos(φ)]);
D[3](φ) := matrix([cos(φ),sin(φ),0],[-sin(φ),cos(φ),0],[0,0,1]);

/* Kugelkoordinanten */
D[12](θ,φ):= matrix([ cos(θ)*cos(φ), cos(θ)*sin(φ), -sin(θ)],
                    [       -sin(φ),        cos(φ),     0  ],
                    [ sin(θ)*cos(φ), sin(θ)*sin(φ),  cos(θ)]);

coord: [[ φ[1](t), φ[2](t), φ[3](t)],
        [δφ[1]   ,δφ[2]   ,δφ[3]   ]];
q: funmake('matrix,makelist([coord[1][i]],i,1,3));

abbr: makelist(diff(φ[i](t),t)=ω[i](t),i,1,3);

params: [
  I[y] =      m       * 3/20*( R^2+4*H^2),
  I[z] =      m       * 3/10*  R^2,
   m   = ρ*%pi*R^2*H/3           ];
params: append(subst(params[3], [params[1], params[2]]),[params[3]]);
params: [params, makelist(solve(params[i], [H^3,R^4,R^2][i])[1],i,1,3)];

Equations of Motion

Die Gleichgewichtsbedingungen für den starren Kreisel (die virtuelle Formänderungenergie $\delta \Pi$ ist Null) kommen aus

${\begin{array}{lll}\delta W&=&\displaystyle \sum _{i}({\vec {F}}_{i}\cdot \delta r_{i})-\rho \int _{V}{\ddot {\vec {r}}}_{P}\cdot \delta {\vec {r}}_{P}\\&{\stackrel {!}{=}}&0\end{array}}$,

wobei wir nur eine Kraft F - die Gewichtskraft $mg(-{\vec {e}}_{3})$ - haben und V das Kreisel-Volumen ist.

Mit dem Ortsvektor zu einem Punkt des Kreisels

${\vec {r}}_{P}=\left(r\;\;0\;\;z\right)\cdot {\underline {\underline {D}}}_{3}(\alpha )\cdot {\underline {\underline {D}}}_{0\to K}(\varphi _{1},\varphi _{2},\varphi _{3})\cdot \left({\begin{array}{c}{\vec {e}}_{1}\\{\vec {e}}_{2}\\{\vec {e}}_{3}\end{array}}\right)$

können wir nun die virtuelle Gesamtarbeit des Systems ausrechnen. Die Parameter mit R und H ersetzen wir durch die oben definierten Abkürzungen und erhalten die gekoppelten Bewegungsgleichungen

Fehler beim Parsen (Unbekannte Funktion „\begin{pmatrix}“): {\displaystyle \begin{pmatrix}{I_y} & 0 & 0\\ 0 & \left( 1-{{\sin{\left( {{\phi }_1}(t)\right) }}^{2}}\right) {I_z}+{{\sin{\left( {{\phi }_1}(t)\right) }}^{2}} {I_y} & \cos{\left( {{\phi }_1}(t)\right) } {I_z}\\ 0 & \cos{\left( {{\phi }_1}(t)\right) } {I_z} & {I_z}\end{pmatrix} \cdot \ddot{\underline{\varphi}} + \begin{pmatrix}\left( {{{{\omega }_2}}^{2}} \cos{\left( {{\phi }_1}\right) } \sin{\left( {{\phi }_1}\right) }+{{\omega }_2} {{\omega }_3} \sin{\left( {{\phi }_1}\right) }\right) {I_z}-{{{{\omega }_2}}^{2}} \cos{\left( {{\phi }_1}\right) } \sin{\left( {{\phi }_1}\right) } {I_y}\\ \left( -2 {{\omega }_1} {{\omega }_2} \cos{\left( {{\phi }_1}\right) } \sin{\left( {{\phi }_1}\right) }-{{\omega }_1} {{\omega }_3} \sin{\left( {{\phi }_1}\right) }\right) {I_z}+2 {{\omega }_1} {{\omega }_2} \cos{\left( {{\phi }_1}\right) } \sin{\left( {{\phi }_1}\right) } {I_y}\\ -{{\omega }_1} {{\omega }_2} \sin{\left( {{\phi }_1}\right) } {I_z}\end{pmatrix} = \begin{pmatrix}-\frac{\displaystyle 2 H g m}{3} \sin{\left( {{\phi }_1}\right)\\ 0\\ 0\end{pmatrix} }

Dieses System von gewöhnlichen Differentialgleichung müssen wir nach den Winkelbeschleunigungen lösen - und das geht nur, wenn die Massenmatrix regulär ist. Wir prüfen das anhand der Systemdeterminante

$\det {\underline {\underline {M}}}=\cos(\phi _{1})^{2}\;I_{y}^{2}\;I_{z}$

Für den Kippwinkel muss also cos(φ₁)≠0 oder 0 < φ₁ < 90° gelten. Das können wir für unsere Problemstellung gut einhalten.

/*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
/* local vector to some material point with coordinates φ[i](t), i=1,2,3 */
/* trafo, order of rotations: y, x', z'' */
r[p]  : matrix([r,0,z]).D[3](α).D[3](φ[3](t)).D[12](φ[1](t),φ[2](t));
δr[p] : sum(subst([ε=0],diff(subst([coord[1][i]=coord[1][i]+ε*coord[2][i]],r[p]),ε)),i,1,3);

/*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
/* virtual work of d'Alembert forces */ 
δW[a] :-ρ*diff(r[p],t,2).δr[p]$
/* integrate over body               */
δW[a] : integrate(integrate(integrate(r*δW[a], α,0,2*%pi), r,0,R*(z/H)), z,0,H)$
δW[a] : expand(expand(expand(expand(expand(expand(expand(δW[a])))))))$
δW[a] : expand(subst(params[2],δW[a]));

/*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
/* virtual work of external (gravitational) force */ 
r[m] : subst([r=0, z=2*H/3], r[p]);
δr[m] : sum(subst([ε=0],diff(subst([coord[1][i]=coord[1][i]+ε*coord[2][i]],r[m]),ε)),i,1,3);
δW[g] : m*matrix([0,0,-g]).δr[m];
δW[g] : expand(δW[g]);

Solving

Mit der Spaltenmatrix der Zustandsgrößen

${\underline {q}}(t)=\left({\begin{array}{c}\varphi _{1}(t)\\\varphi _{2}(t)\\\varphi _{3}(t)\\\omega _{1}(t)\\\omega _{2}(t)\\\omega _{3}(t)\\\end{array}}\right)$

lösen wir die gewöhnlichen Differentialgleichungen

${\underline {\dot {q}}}(t)={\underline {f}}({\underline {q}}(t))$

Dazu formulieren wir die Bewegungsgleichungen zunächst in Maxima und übertragen sie dann in ein Matlab^©-Script. Die Bewegungsgleichungen machen wir mit der Zeit

$T={\sqrt {\frac {\displaystyle 2Hmg}{3I_{y}}}}$

dimensionslos (die Winkel selbst sind ja bereits dimensionslos). Die dimensionslose Zeit $\tau =t/T$.

/*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
/* equations of motion */
eom: makelist(coeff(-δW[a],coord[2][row]),row,1,3);

/* mass matrix */
M: makelist(makelist(coeff(eom[row],diff(coord[1][col],t,2)),col,1,3),row,1,3);
M: trigsimp(funmake('matrix,M));
/* M^(-1) */
Mi : trigsimp(invert(M));

/* the rest ... */
gyr: trigsimp(expand(eom - M.diff(q,t,2)));
P:  makelist(coeff(-δW[g],coord[2][row]),row,1,3);

Matlab^©-files

Folder Structure

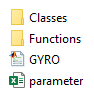
Die Datei-Struktur zeit das Skript GYRQ.m. Classes und Functions sind in den jeweiligen Ordnern. Die Excel-Datei hält alle System-Parameter.

Den komplette Quellcode zu diesem Programm können Sie über dieses ZIP-File rechts herunterladen.

archive

download compressed archive →

Postprocessing

Die Ergebnisse der numerischen Integration tragen wir für die Winkel φ₁(t), φ₂(t) sowie für die Winkelgeschwindigkeiten ω₁(t), ω₂(t) auf. Es folgen noch die Trajektorie des Mittellinien-Endpunkts des Kreisels und die Phasendiagramme.

Winkel	Winkelgeschwindigkeit
Trajektorie	Phasendiagramme

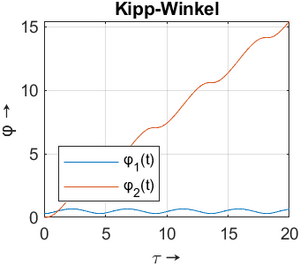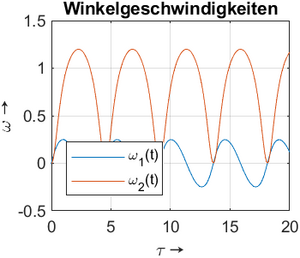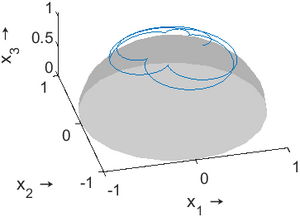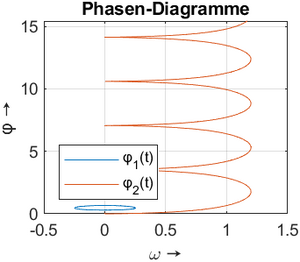... in Matlab (vgl. zip-Datei)

Nachtrag

Meist linearisiert man die Bewegungsgleichungen, indem man von kleinen Kippwinkeln ausgeht (φ₁<<1, φ₂<<1). Für den Kreisel gilt außerdem ω₁<<ω₃, ω₂<<ω₃ so dass man außerdem ω₃ = constant setzten darf. Damit erhalten wir die "übliche" vereinfachte Bewegungsgleichung

${\begin{pmatrix}{I_{y}}&0&0\\0&{I_{y}}&0\\0&0&{I_{z}}\end{pmatrix}}\cdot {\ddot {\underline {\varphi }}}+\omega _{3}\cdot {\begin{pmatrix}0&-I_{z}&0\\I_{z}&0&0\\0&0&0\end{pmatrix}}\cdot {\dot {\underline {\varphi }}}={\frac {\displaystyle 2}{\displaystyle 3}}Hmg{\begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}}\cdot {\underline {\varphi }}$

<syntaxhighlight lang="lisp" line start=1> /*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/ /* simplify */ gyrs: trigsimp(subst(abbr,gyr)); smalls: [ω[1](t)=ε*ω[1](t),ω[2](t)=ε*ω[2](t)]; gyrs: subst([ε^2=0,ε=1],expand(subst(smalls,gyrs)));

G: makelist(makelist(coeff(expand(gyrs[row][1]/ω[3](t)),ω[col](t)),col,1,3),row,1,3); G: trigsimp(funmake('matrix,G));

Dieses lineare System von gewöhnlichen Bewegungsgleichungen kann man dann hervorragend als Eigenwertproblem analysieren.

---

Links

• ...

Literature

• ...