Sources/Lexikon/Quaternionen für Drehungen
Zur Navigation springen
Zur Suche springen
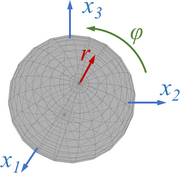
3D visualization einer Rotation bzgl. der Euler-Axe um den Winkel ϕ.
Einheits-Quaternionen sind ein probates Werkzeug, um die räumliche Orientierung von Körpern zu beschreiben und räumliche Drehungen durchzuführen.

Dabei wird die Rotation durch einen Drehwinkel ϕ um eine Rotationsachse
beschreiben. Bei Einheits-Quaternionen gilt
- .
Die Rotation wird dann durch das [Quadruple]
- Fehler beim Parsen (Syntaxfehler): {\displaystyle \displaystyle \underline{q} = \left\[\cos\varphi, r_x\cdot\sin\varphi, r_y\cdot\sin\varphi, r_z\cdot\sin\varphi \right\]}
erfasst.
Die Transformationsmatrix können wir dann durch
abgebildet.