Werkzeuge/Beschreibung physikalischer Systeme/Dimensionen und Einheiten
Schreibweise
Die Dimension einer physikalischen Größe erfasst man durch
So ist
oder, abgekürzt
Basis-Einheiten nach dem SI-System sind
- Meter (m),
- Kilogramm (kg),
- Sekunde (s),
- Ampere (A),
- Kelvin (K),
- Mol (mol) sowie
- Candela (cd)
Von diesen sieben brauchen wir hier nur die ersten drei.
Weitere Einheiten lassen sich auf diese drei zurückführen und umrechnen:
- ,
oder
- .
Im Computer können wir keine Einheiten brauchen. Wir könnten alle Parameter in den SI-Basiseinheiten ausdrücken - dann müssen sich die Einheiten herauskürzen. Das geht bei realen Problemen häufig schief, weil die dann in den Systemmatrizen stehenden numerische Werte oft um mehrere Größenordnungen unterschiedliche Werte haben.
Beispiel:
Die numerischen Werte in der Randbedingung des Euler-Bernoulli-Balkens
- für das Moment sind von der Größenordnung 10^6;
- für die Verschiebung/Verdrehung sind von der Größenordnung 1.
Dimensionslos-Machen von Bewegungsgleichungen
Wir suchen nach Koordinaten der Bewegung, die keine Einheit mehr haben und deren Werte von der Größenordnung "1" sind. Das klappt nicht immer, aber oft.
Vorgehensschema:
- alle dimensionsbehafteten Parameter und Koordinaten durch dimensionslose Größen und Bezugsgrößen ersetzen;
- die Bezugsgrößen aus den Bewegungsgleichungen herauskürzen → die Bewegungsgleichung sieht wieder wie ursprünglich aus;
- Bezugsgrößen "passend" wählen;
- die numerischen Werte aller dimensionslosen Parameter berechnen und in die Bewegungsgleichungen einsetzen;
- Bewegungsgleichungen lösen.
Beispiel:
Aufgabenstellung
Wir lassen eine Kugel im Erdschwerefeld aus der Höhe H und ohne Anfangsgeschwindigkeit fallen.
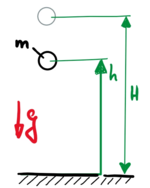
Die Bewegungsgleichung des Systems mit der nichtlinearen Kontaktkraft K(h) in h(t) lautet:
- ,
Dimensionslose Koordinate
Eine dimensionslose Koordinate bekommen wir, wenn wir h durch eine passende Bezugslänge lBez teilen, also
- ,
Die zweite Ableitung nach der Zeit bringt uns allerdings wieder eine Dimension - hier die Zeit - hinein. Mit der neuen, dimensionslosen Zeit τ
- ,
und den dimensionslosen Parametern
- ,
lautet die neue Bewegungsgleichung nun
- ,
Das sieht sehr kompliziert aus - löst sich aber gleich in Wohlgefallen auf. Zunächst dürfen wir nur drei Beszugsgrößen unabhängig voneinander wählen, also könnten wir
- ,
ersetzen und erhalten - nach der Division durch die Bezugskraft
- ,
Das ist nun wiederum die Form der Ausgangs-Bewegungsgleichung - nur, dass hier jetzt andere Zahlenwerte stehen.
Wahl der Bezugsgrößen
Es ist praktisch
- ,
zu wählen - denn dann wird der Wert von der dimensionslosen Koordinate h(t)/H zwischen 0 und 1 sein, die Dauer einer Periode des Vorgangs wird fast 2 sein (wenn die Stoßdauer sehr kurz ist).
Mit den Systemparametern
- ,
ist z.B. der Zahlenwert für die dimensionslose Erdbeschleunigung nun
- ,
Bewegungsgleichungen lösen
Die Bewegungsgleichung können wir nun als ODE 1ster Ordnung schreiben als
- ,
und im Zeitbereich mit den Anfangsbedingungen
- ,
lösen. Im Zeitbereich finden wir die Lösung
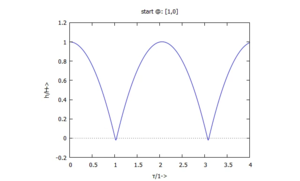
und die entspricht - mit der Anfangs-Höhe "1" und der Periodendauer von (fast) "2" - genau unseren Vorstellungen!