Gelöste Aufgaben/UEBA
Aufgabenstellung
Wie man die Sensoren eines Smartphones für Messungen einsetzt, zeigen wir hier.
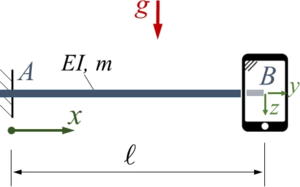
Hier soll der Elastizitätsmodul des Stab-Materials mit Hilfe eines Biegeversuchs bestimmt werden. Der Stab der Länge ℓ hat einen quadratischen Querschnitt der Höhe h und die Masse m. Für die Messung nutzen Sie als Sensor ihr Smartphone, das Ihnen die statische Beschleunigung ay, az in y- und z-Richtung angibt.
Sie haben Ihre Standard-Lösungen für den Euler-Bernoulli-Balken zu Hause vergessen und müssen sich mit einer Näherungslösung für den Balken nach dem Verfahren von Rayleigh-Ritz zufrieden geben.
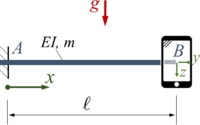
Für den Versuch wird der Balken wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt, die Masse des Smartphones sei vernachlässigbar.
Gesucht ist die Lösung mit dem Ansatz von Rayleigh-Ritz und zwei Trial-Functions.
Gegeben: ℓ=3 m, m=28 kg, g=9.81 m/s2, h=10 cm,
ay = 0.9793658 m/s2, az= 9.7609909 m/s2
Lösung mit Maxima
Smartphones haben eine Reihe von Sensoren eingebaut - und die man kann als Ingenieur prima gebrauchen ...
Ein Erklärungsvideo zu Beschleunigungs-Sensoren finden Sie hier.
Header
Das Rayleigh-Ritz-Verfahren ist hier ein bisschen unter der experimentellen Bestimmung von Parametern des Systems "vergraben".
Der Lösungsweg ist aber der gleiche wie gewohnt.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2020-01-13 */
/* ref: TMC */
/* description: Rayley-Ritz-Solution for EBB */
/* with "Smartphone" */
/* see https://youtu.be/KZVgKu6v808 */
/*******************************************************/
/*******************************************************/
/* declare variational variables - see 6.3 Identifiers */
declare( "ℓ", alphabetic);
declare( "φ", alphabetic);
declare( "Φ", alphabetic);
declare( "ŵ", alphabetic);
System-Parameters
Die Streckenlast auf den Balken ist
und wir arbeiten mit der dimensionslosen Länge
- .
/* system parameters */
params: [q[0]=m*g/ℓ];
dimless: [x = xi*ℓ];
/* make equations of motion dim'less with load case #1 from Gross e.a., same as UEBI */
reference : [ŵ = q[0]*ℓ^4/(8*EI), Phi[ref] = q[0]*ℓ^3/(6*EI), M[ref] = m*g*ℓ, Q[ref] = m*g];
Formfunctions
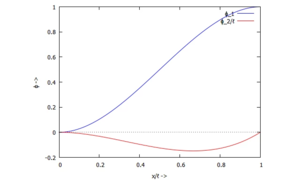
Als Ansatzfunktion für die Näherungslösung verwenden wir
- .

Die Trial-Functions ϕi erfüllen dabei die Bedingungen
und
/************************************************************/
/* Rayleigh-Ritz */
/* trial function */
trial: w(xi) = sum(C[j]*xi^(j),j,2,3);
trial: expand(subst(solve([subst([xi=1],subst(trial,w(xi)))= W,subst([xi=1],diff(subst(trial,w(xi)),xi)/ℓ)= Φ],[C[2], C[3]])[1],trial));
X : [W,Φ];
phi : makelist(coeff(subst(trial,w(xi)),X[i]),i,1,2);
plot2d([phi[1],phi[2]/ℓ],[xi,0,1], [xlabel, "x/ℓ ->"], [ylabel, "ϕ ->"], [legend, "ϕ_1", "ϕ_2/ℓ"]);
Potential Energy
Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems
- ,
wobei Π die Formänderungsenergie ist und A die Arbeitsfunktion der äußeren Last q0.
Es ist
- .
Π und A setzen wir in U ein und schreiben die skalare Gleichung in Matrizenform an. Dabei müssen wir
beachten. Mit den gesuchten Größen
erhalten wir für das Potential
wobei für die Koeffizienten der Matrix K
gilt und die rechten Seite P
- .
| ✔ Matlab© und Polynome: |
| Alle verwendeten Funktionen in diesem Beispiel sind Polynome. Matlab© bietet für die Manipulation von Polynomen eine Klasse von Functions an, die hier sehr hilfreich sind: |
/* define potential energy of system */
PMPE : [U = Pi - A,
Pi = 1/2*ℓ*'integrate(EI*'diff(w(xi),xi,2)^2/ℓ^4,xi,0,1),
A = ℓ*'integrate(q[0]*w(xi),xi,0,1)];
PMPE: subst(dimless,subst(params,subst(trial,PMPE)));
PMPE: subst(PMPE[3],subst(PMPE[2], PMPE[1]));
PMPE : ev(PMPE,nouns);
Solving
Die Gleichgewichtsbedingungen
sind erfüllt, wenn
- .
Dieses lineare Gleichungssystem hat die Lösung
- .
Zum Vergleich schauen wir jetzt bei der analytischen Lösung des Problems nach:
- .
Und sehen: unsere Lösung nach Rayleigh-Ritz stimmt am Rand exakt mit der analytischen Lösung überein, es ist
- !
/*******************************************************/
/* equilibreium condition */
equilibrium : makelist(diff(subst(PMPE, U),X[j]) = 0,j,1,2);
ACM : augcoefmatrix(equilibrium,X);
print(submatrix(ACM,3),"*",transpose(X),"=",-col(ACM,3))$
/*******************************************************/
/* solve */
sol: ratsimp(solve(equilibrium,X))[1];
Post-Processing
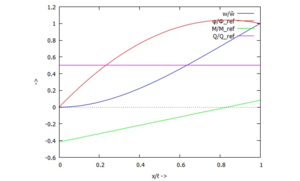
Die Näherungslösung für Auslenkung w(x), Kippwinkel ϕ(x), Moment M(x) und Querkraft Q(x) können wir jetzt auftragen. Dafür verwenden wir die weiteren Referenzgrößen
und tragen die Lösungen dimensionslos auf:
Für unsere Fragestellung schreiben wir die Lösung um als
und bestimmen uns den Drehwinkel aus den gemessenen statischen Beschleunigungen (vgl. Bild oben). Dabei ist
- .
| 🧨 Warum nehmen wir nicht die z-Komponente der Beschleunigung?: |
| Die az-Komponente können wir nicht gebrauchen weil
|
Da für kleine Winkel sin(Φ) ≈ Φ gilt, ist
Wir berechnen die gesuchte Materialkonstante mit
zu
- .
/************************************************************/
/* post-processing */
fcts: ratsimp( subst(params,subst(reference,subst(sol,subst(trial,w(xi)/ŵ)))));
fcts: makelist( [ŵ,ŵ,-EI*ŵ,-EI*ŵ][i+1]*diff(fcts,xi,i)/ℓ^i,i,0,3);
fcts: makelist(fcts[i]/[ŵ, Phi[ref], M[ref], Q[ref]][i], i,1,4);
fcts: subst(params,subst(reference,fcts));
plot2d(fcts, [xi,0,1], [xlabel, "x/ℓ ->"], [ylabel, " ->"],
[legend, "w/ŵ", "φ/Φ_ref", "M/M_ref", "Q/Q_ref"]);
Links
- ...
Literature
- ...