Gelöste Aufgaben/Kw96

Aufgabenstellung

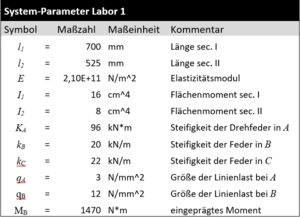
Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten q_A in A und q_B in B sowie dem Moment M_B in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l₁ bzw. l₂ sowie den Flächenmomenten I₁ bzw. I₂. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit K_A, die Federn in B und C sind Translationsfedern mit den Steifigkeiten k_B, k_C.

Lageplan

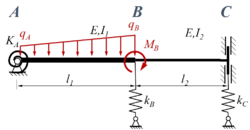
Gesucht ist die FEM Lösung für den Euler-Bernoulli-Balken unter Verwendung von zwei Finiten Elementen.

Systemparameter

Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter:

tmp

Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "FEM-Formulierung für den Euler-Bernoulli-Balken".

Header

Text

1+1

tmp

System-Parameter sind:

$\begin{array}{l}{q}_A=3000\frac{N}{m},\\ {\ell }_1=\frac{7\cdot m}{10},\\ {{E}{I}}_1=33600N{m}^2,\\ {\ell }_2=\frac{21}{40}m,\\ {{E}{I}}_2=16800N{m}^2,\\ K_A=96000Nm,\\ k_C=\frac{256}{229}\cdot k_B,\\ k_B=\frac{256}{229}Nm,\\ q_B=12000\frac{N}{m},\\ M_B=1470Nm\end{array}$

Declarations

Text

1+1

tmp

Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades:

$\mathrm{w}\left(\xi \right):=c_3\cdot {\xi }^3+c_2\cdot {\xi }^2+c_1\cdot \xi +c_0$

An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen:

$\begin{array}{l}{c}_0=W_{i-1},\\ \frac{c_1}{l_i}={\mathrm{\Phi }}_{i-1},\\ c_3+c_2+c_1+c_0=W_i,\\ \frac{c_1+2\cdot c_2+3\cdot c_3}{l_i}={\mathrm{\Phi }}_i\end{array}$

Trial-Functions

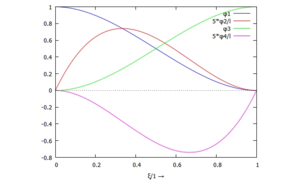
Damit ist die Ansatzfunktion des Finiten Elements mit den vier Knotenvariablen

$w(\xi )={\ell }_i\cdot {\mathrm{\Phi }}_i\cdot (\xi -1)\cdot {\xi }^2+W_{i-1}\cdot {(\xi -1)}^2\cdot (1+2\cdot \xi )-W_i\cdot {\xi }^2\cdot (2\cdot \xi -3)+{\mathrm{\Phi }}_{i-1}\cdot {\ell }_i\cdot {(\xi -1)}^2\cdot \xi$

Formfunctions

Text

1+1

tmp

So sind die Element-Steifigkeitsmatrix

${\underset{\_}{\underset{\_}{K}}}_i=\frac{E{I}_i}{{\ell }_i^3}\left(\begin{array}{cccc}12& 6\cdot {\ell }_i& -12& 6\cdot {\ell }_i\\ 6\cdot {\ell }_i& 4\cdot {\ell }_i^2& -6\cdot {\ell }_i& 2\cdot {\ell }_i^2\\ -12& -6\cdot {\ell }_i& 12& -6\cdot {\ell }_i\\ 6\cdot {\ell }_i& 2\cdot {\ell }_i^2& -6\cdot {\ell }_i& 4\cdot {\ell }_i^2\end{array}\right)$

die Koordinaten des FE-Modells - hier für das Element "1":

$\underset{\_}{Q}=\left(\begin{array}{c}{\mathrm{\Phi }}_0\\ W_1\\ {\mathrm{\Phi }}_1\\ W_2\end{array}\right)$.

Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu

${\underset{\_}{\underset{\_}{K}}}_0=\left(\begin{array}{cccc}{K}_A+\frac{4{{E}{I}}_1}{{\ell }_1}& -\frac{6{{E}{I}}_1}{{\ell }_1^2}& \frac{2{{E}{I}}_1}{{\ell }_1}& 0\\ -\frac{6{{E}{I}}_1}{{\ell }_1^2}& k_B+\frac{12{{E}{I}}_2}{{\ell }_2^3}+\frac{12{{E}{I}}_1}{{\ell }_1^3}& \frac{6{{E}{I}}_2}{{\ell }_2^2}-\frac{6{{E}{I}}_1}{{\ell }_1^2}& -\frac{12{{E}{I}}_2}{{\ell }_2^3}\\ \frac{2{{E}{I}}_1}{{\ell }_1}& \frac{6{{E}{I}}_2}{{\ell }_2^2}-\frac{6{{E}{I}}_1}{{\ell }_1^2}& \frac{4{{E}{I}}_2}{{\ell }_2}+\frac{4{{E}{I}}_1}{{\ell }_1}& -\frac{6{{E}{I}}_2}{{\ell }_2^2}\\ 0& -\frac{12{{E}{I}}_2}{{\ell }_2^3}& -\frac{6{{E}{I}}_2}{{\ell }_2^2}& k_C+\frac{12{{E}{I}}_2}{{\ell }_2^3}\end{array}\right)$

Wie das geht, steht in Abschnitt Finite Elemente Methode.

Equilibrium Conditions

Text

1+1

tmp

Die Knotenvariablen sind damit

$\begin{array}{ll}{W}_0=0& \\ {\mathrm{\Phi }}_0=0.00624& \\ W_1=0.00657m& \\ {\mathrm{\Phi }}_1=0.0123& \\ W_2=0.00846m& \\ {\mathrm{\Phi }}_2=0& \end{array}$

Solving

Text

1+1

tmp

Biegelinie w(x)

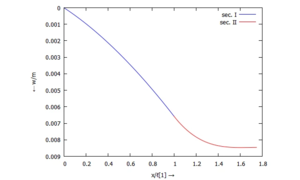
Die Biegelinie des Balkens sieht damit so aus:

Post-Processing

Text

1+1

---

Links

• ...

Literature

• ...