Gelöste Aufgaben/Kw53

Aufgabenstellung

Eine Brücke ABC der Masse m_B und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit K_C mit dem Lager verbunden. In A steht eine Person der Masse m_A.

Lageplan (wie Kw50)

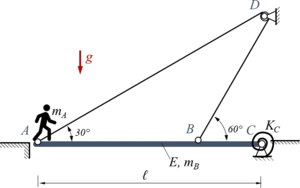
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Verfahren von Rayleigh-Ritz (EBB) an - hier ohneLagrange-Multiplikator für die geometrische Zwangsbedingung.

Dies ist eine Näherungslösung zu Kw50.

Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:

$\begin{array}{ll}{K}_C=& 5\frac{EI}{{\ell }_0}\\ m_A=& \frac{m_B}{5}\end{array}$

Lösung mit Maxima

In dieser Aufgabe berechnen wir eine Näherungslösung nach dem Verfahren von Rayleigh-Ritz (EBB) zu Kw50.

Alle Überlegungen zur Geometrie des Systems übernehmen wir.

tmp

Für die Lösung nutzen wir hier das Ritz-Verfahren. Die geometrischen Zwangsbedingungen arbeiten wir direkt in die Trial-Functions ein.

Header

text

1+1

tmp

Header

text

1+1

tmp

Wir arbeiten mit den selben Parametern und Bezugslängen, wie in Kw50.

Declarations

text

1+1

tmp

Nach "Ritz" wählen wir zwei Trial-Functions über die gesamte Stablänge. Als zugehörige, gesuchte Koordinaten wählen wir die Auslenkung in A und die Verdrehung in C, also

$\underset{\_}{Q}=\left(\begin{array}{c}{W}_A\\ {\mathrm{\Phi }}_C\end{array}\right)$.

Die Trial-Functions müssen dann diesen geoemtrischen Zwangsbedingungen genügen:

$\begin{array}{l}w(0)=W_A\\ w({\ell }_1)=W_B\text{ mit }{W}_B=-\frac{W_A}{\sqrt{3}}\\ \frac{dw}{dx}{|}_{x=\ell }={\mathrm{\Phi }}_C\end{array}$.

Mit einem Polynom 3-ten Grades als Ansatz ist also unser Näherungsansatz für die Auslenkung dann

$\tilde{w}(\xi )=\sum _{i=1}^2{Q}_i\cdot {\varphi }_i(\xi )$

mit den Trial-Functions

$\begin{array}{lll}{\varphi }_1=& -& \frac{1}{2}((3^{\frac{5}{2}}+3){\xi }^3+(-23^{\frac{5}{2}}-8){\xi }^2+(3^{\frac{5}{2}}+7)\xi -2)\\ {\varphi }_2=& & {\ell }_o\cdot (3{\xi }^3-5{\xi }^2+2\xi )\end{array}$.

Und so sehen sie aus, unsere zwei Trial-Functions:

Trial Functions

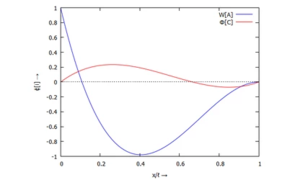
Formfunctions

text

1+1

tmp

Die Potentiale aus Elastischen Energien und Arbeitsfunktion der Gewichtskräfte sind

$\begin{array}{lll}U=& & \frac{1}{2}\cdot \underset{0}{\overset{\ell }{\int }}EI{w}^{\prime }{\text{'}}^{2}dx+\frac{1}{2}\cdot K_C\cdot {\mathrm{\Phi }}_C^2\\ & -& \underset{0}{\overset{\ell }{\int }}{q}_{0}wdx-m_{A}g{W}_A\end{array}$.

Einsetzten der Trial-Functions liefert

$U=\frac{1}{2}(W_A,{\mathrm{\Phi }}_C)\underset{:=\underset{\_}{\underset{\_}{A}}}{\underbrace{\left(\begin{array}{cc}\frac{(83^{\frac{5}{2}}+262){E}{I}}{{\ell }_0^3}& -\frac{(53^{\frac{5}{2}}+17){E}{I}}{{\ell }_0^2}\\ -\frac{(53^{\frac{5}{2}}+17){E}{I}}{{\ell }_0^2}& \frac{28{E}{I}+{\ell }_0{K}_C}{{\ell }_0}\end{array}\right)}}\left(\begin{array}{c}{W}_A\\ {\mathrm{\Phi }}_C\end{array}\right)-(W_A,{\mathrm{\Phi }}_C)\underset{:=\underset{\_}{b}}{\underbrace{\left(\begin{array}{c}{m}_{A}g-\frac{3^{\frac{3}{2}}{q}_0{\ell }_0}{8}+\frac{5q_0{\ell }_0}{24}\\ \frac{q_0{\ell }_0^2}{12}\end{array}\right)}}$

Potentials

text

1+1

tmp

Nach dem Minimum Prinzip hat das Potential U ein Minimum - das Sytem ist im Gleichgewicht, wenn

$\underset{\_}{\underset{\_}{A}}\cdot \underset{\_}{Q}=\underset{\_}{b}$.

In den System-Matrizen stehen hier

$\underset{\_}{\underset{\_}{A}}=\left(\begin{array}{cc}\frac{386.7\cdot {E}{I}}{{\ell }_0^3}& -\frac{94.9\cdot {E}{I}}{{\ell }_0^2}\\ -\frac{94.9\cdot {E}{I}}{{\ell }_0^2}& \frac{{\ell }_0\cdot K_C+28\cdot {E}{I}}{{\ell }_0}\end{array}\right)$ und

$\underset{\_}{b}=\left(\begin{array}{c}{m}_{A}g-0.4\cdot q_0\cdot {\ell }_0\\ 0.08\cdot q_0\cdot {\ell }_0^2\end{array}\right)$.

Equilibrium Conditions

text

1+1

tmp

Das Lösen des Gleichungssystems liefert dann

$\left(\begin{array}{c}{W}_A\\ {\mathrm{\Phi }}_C\end{array}\right)=\frac{m_{B}g{\ell }_0^3}{3EI}\left(\begin{array}{l}-3.78{10}^{-5}\\ 0.00747\frac{1}{\ell }\end{array}\right)$.

Solving

text

1+1

tmp

Post-Processing

Und die Ergebnisse können wir uns anschauen ...

... für w(x):

Auslenkung w(x)

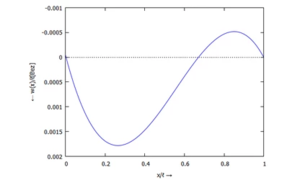
... für Φ(x):

Kippwinkel Φ(x)

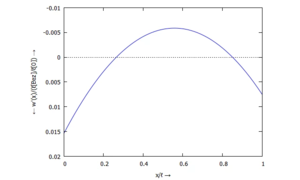
... für M(x):

Biegemoment M(x)

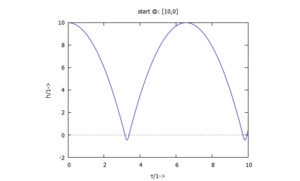
... für Q(x):

Querkraft Q(x)

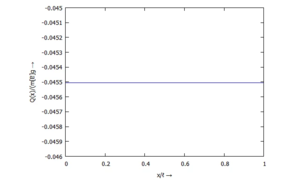
/* Post-Processing                                    */
w : subst([x=xi*ℓ[0]],subst(geometry,subst(sol, sum(Q[j]*phi[j],j,1,3))));

fcts: [         w             ,
           diff(w,xi  )/ℓ[0]  ,
       -EI*diff(w,xi,2)/ℓ[0]^2,
       -EI*diff(w,xi,3)/ℓ[0]^3];
fcts: float(subst(geometry,expand(fcts)))$ 
facts: [1/ℓ[Bez], ℓ[0]/ℓ[Bez], 1/(m[B]*g*ℓ[0]), 1/(m[B]*g)];
 
textlabels : ["← w(x)/ℓ[Bez]", "← w'(x)/(ℓ[Bez]/ℓ[0]) →", "M(x)/(m[B]*g*ℓ) →", "Q(x)/(m[B]g →"];
for i: 1 thru 4 do(
  f : expand(subst(dimless,facts[i]*fcts[i])),
  preamble: if i<=2 then "set yrange [] reverse" else "set yrange []",
  plot2d(f, [xi,0,1], [legend, false],
                      [gnuplot_preamble, preamble],
                      [xlabel, "x/ℓ →"],
                      [ylabel, textlabels[i]]))$

---

Links

• Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
• Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
• Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)

Literature

• ...