Gelöste Aufgaben/Kw30
Aufgabenstellung
Oft stößt man in unscheinbaren Aufgabenstellungen auf unerwartete Hindernisse - so in dieser Aufgabe eines mathematischen Pendels, die auf eine Bewegungsgleichung mit periodischen Koeffizienten führt.
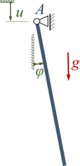
Das Pendel der Masse m und Länge ℓ der Aufgabe hat einen in A senkrecht mit u(t) periodisch bewegten Aufhängepunkt.
Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen.
Gegeben sind
- m, ℓ, g sowie
Lösung mit Maxima
tmp
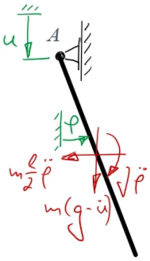
Aus dem Freikörperbild erhalten wir die Bewegungsgleichung
mit
.
Wir linearisieren und erhalten mit
die lineare Differentialgleichung mit perdiodischen Koeffizienten
.
Das ist eine Grundform der Mathieuschen Differentialgleichung - die wir noch in dimensionslose Form bringen wollen. Dazu soll die zugeordnete gewöhnliche Differentialgleichung mit konstanten Koeffizienten, also für
,
in dimensionsloser Schreibweise und für einfache Parameter-Konstellationen die Periodendauer "1" haben. Das erreichen mit der dimensionslosen Zeit
und den dimensionslosen Parametern
.
Damit ist
.
Für Λ=1 ist das wie gewünscht eine Bewegungsgleichung mit der Periodendauer "1":
.
Equations of Motion
Text
1+1
tmp
Für die Stabilität der Bewegungsgleichung brauchen wir den Satz von Floquet-Ljapunow und die Fundamentalmatrix Φ. Zunächst schreiben wir die Bewegungsgleichung als Differentialgleichung erster Ordnung als
bzw. als
.
Durch den Zeit-periodischen Koeffizienten in τ hat diese Bewegungsgleichung keine "einfachen" Lösungen der Form eλt mehr. Statt dessen untersuchen wir die Stabilität anhand der Fundamentalmatrix Φ*, in der zwei Fundamentalösungen
mit
und
stehen.
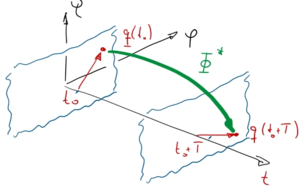
Wir interpretieren also die Fundamentalmatrix Φ* als Abbildungsvorschrift, um die Anfangsbedingungen q(0) über das Zeitintervall - hier T = 1 - hinweg abzubilden.
Die Eigenwerte μi der Fundamentalmatrix heißen
- charakteristische Multiplikatoren.
Die charakteristischen Exponenten sind
- .
Damit Lösungen der Bewegungsgleichung stabil sind, muss
für alle Eigenwerte gelten. Die Fudnamentalmatrix erhalten wir am besten durch die numerische Lösung der Bewegungsgleichung als Anfangswertproblem - hier mit dem Runge-Kutta-Verfahren 4.ter Ordnung - z.B. für
Durch zweifache Lösung des Anfangswertproblems finden wir
.
Die Fundamentalmatrix hat die Eigenwerte
und besitzt damit einen Eigenwert, dessen Betrag größer als "1" ist - die Lösung ist instabil.
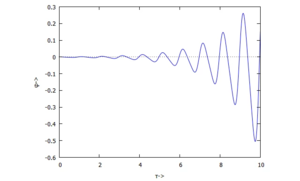
Das können wir prüfen, indem wir uns die numerische Lösung im Zeitbereich anschauen:
- der Winkel der Auslenkung wächst (exponentiell) mit der Zeit.
Solve and Check for Stability of Solution
Text
1+1
tmp
Diese Untersuchung können wir nun für eine Reihe von Parameter-Konstellationen wiederholen und den größeren der beiden charakteristischen Exponenten jeweils auftragen.
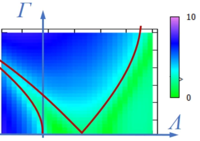
Wir untersuchen den Bereich
und tragen die Werte des Exponenten ρ farbig kodiert auf:
Bei genauerer Analyse können wir die stabilen (grün) von den instabilen Parameter-Bereichen durch eine rote Linie trennen.
Dies ist ein Ausschnitt der Ince-Struttschen Karte. Sie gibt die Stabilität der Lösungen der Mathieuschen Differentialgleichungen an.
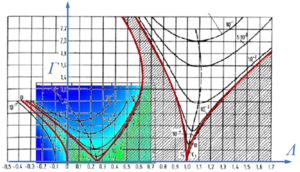
Und so sieht die gesamte Ince-Struttsche Karte aus:
Achtung: hier wurden unterschiedliche Parameterwerte für Λ und Γ verwendet!
Wir erkennen: bei periodischer Erregung des Fußpunktes hat
- das gewöhnliche mathematische Pendel (Λ>0) große Bereiche dynamischer Instabilität!
- das inverse Pendel (Λ<0) Bereiche dynamischer Stabilität!
Ince-Struttsche Karte
Text
1+1
Links
Literature
- ...