Gelöste Aufgaben/Kw29

Aufgabenstellung

In einer Sporthalle wird ein Federball (Punktmasse m) mit einer Anfangsgeschwindigkeit v₀ unter einem Winkel α gegenüber der Horizontalen abgeschlagen. Der Strömungswiderstand des Federballs wird mit

$W=\gamma \cdot v^2$

angegeben, dabei ist γ eine gemessene Größe.

Lageplan

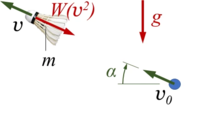
Schreiben Sie die Bewegungsgleichung des Federballs an. Formulieren Sie die Bewegungsgleichung des Federballs in dimensionsloser Form und berechnen Sie die Lösung numerisch als Anfangswertproblem.

Gegeben: g, m, γ, v₀

tmp

Lageplan

Die Koordinaten der Bewegung des Federballs sind

• u(t) in horizontale und
• w(t) in vertikale Richtung.

Als Parameter der Bewegung wählen wir:

$\begin{array}{lll}{h}_0& =2\text{m}& \dots \text{ Anfangshöhe}\\ v_0& =65\text{km/h}& \dots \text{ Anfangsgeschwindigkeit}\\ \end{array}$.

Header

Text

1+1

tmp

Die Bewegungsgleichungen in horizontale und vertikale Richtung sind

$\begin{array}{ll}m\ddot{u}+W\cdot \cos (\alpha )& =0\\ m\ddot{w}+W\cdot \sin (\alpha )& =-mg\end{array}$.

Dabei ist

$\begin{array}{rl}v& =\sqrt{{\dot{u}}^2+{\dot{w}}^2}\\ \cos \alpha & =\frac{\dot{u}}{v}\\ \sin \alpha & =\frac{\dot{w}}{v}\end{array}$.

Als nächstes machen wir die Bewegungsgleichungen dimensionslos mit

• der dimensionslosen Zeit $\tau =\frac{t}{T}$ und
• den dimensionslosen Koordinaten $U=\frac{u}{L}\text{ bzw. }W=\frac{w}{L}$,

dabei sind T = h₀ / v₀ die Bezugszeit und L = h₀' die Bezugslänge.

Die neuen Form der nichtlinearen Bewegungsgleichung ergibt sich dann zu

$\begin{array}{ll}\frac{d^2}{d{\tau }^2}\cdot U& =-\mathrm{\Gamma }\cdot (\frac{d}{d\tau }\cdot U)\cdot \sqrt{{(\frac{d}{d\tau }\cdot W)}^2+{(\frac{d}{d\tau }\cdot U)}^2},\\ \frac{d^2}{d{\tau }^2}\cdot W& =-\mathrm{\Gamma }\cdot (\frac{d}{d\tau }\cdot W)\cdot \sqrt{{(\frac{d}{d\tau }\cdot W)}^2+{(\frac{d}{d\tau }\cdot U)}^2}-G\end{array}$,

die wir numerisch lösen.

Equilibrium Conditions

Text

1+1

tmp

Für Γ=1/2 und α₀ = 30° lösen wir das Problem numerisch, dazu wählen wir als Anfangsbedingungen

$\begin{array}{ll}U(0)& =0\\ W(0)& =1\\ \frac{d}{d\tau }{U|}_{\tau =0}& =\cos {\alpha }_0\\ \frac{d}{d\tau }{W|}_{\tau =0}& =\sin {\alpha }_0\end{array}$.

Solving

Text

1+1

tmp

Die Flugbahn des Federballs erhalten durch den Parameter-Plot mit W(τ) über U(τ).

Flugbahn

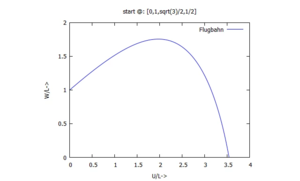
Post-Processing

Text

1+1

---

Links

• ...

Literature

• ...