Gelöste Aufgaben/Kw26

Aufgabenstellung

Ein Aggregat der Masse 2m ist durch zwei Gummifedern wie skizziert gelagert und wird senkrecht durch seine Gewichtskraft und eine äußere Last F=2 H sin(Ω t) belastet.

Lageplan

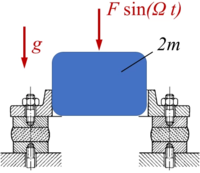
Für dieses System mit einem nichtlineares Federelement soll die Lösung als Anfangswertproblem gefunden und mit der linearen Näherungslösung verglichen werden.

Gesucht sind

• die Lösung der zugeordneten linearisierten Bewegungsgleichung,
• die numerische Lösung des nichtlinearen Problems.

Kennlinie

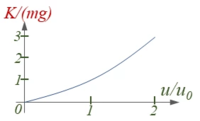
Für die Gummifeder gibt der Lieferant folgende eine Kennlinie an:

Gegeben:

• u₀,
• m, g, H, Ω'

Lösung mit Maxima

Koordinate u

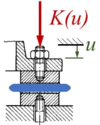
Header

Gummi-Elemente zeigen eine deutliche Nichtlinearität bei großen Auslenkungen. Wie man diese Nichtlinearität bei dynamischer Belastung berücksichtigt, zeige ich Ihnen hier.

/*********************************************************/
/* MAXIMA script                                         */
/* version: wxMaxima 15.08.2                             */
/* author: Andreas Baumgart                              */
/* last updated: 2018-11-27                              */
/* ref: Kw26 (TM-C, Labor 6)                             */
/* description: finds the solution for                   */
/*              the nonlinear IVP                        */
/*********************************************************/

Declarations

Wir berücksichtigen nur die vertikale Bewegung des Aggregats, dafür nehmen wir die Koordinate u:

Als System-Parameter setzten wir an:

• $H=m\;g\;\gamma$
  (Kraft-Amplitude als Vielfaches der Gewichtskraft) und
• ${\begin{array}{l}\displaystyle \Omega ={\frac {2\;\pi }{T_{\Omega }}},\;\\T_{\Omega }=\eta \;T_{0}\end{array}}$
  (Erreger-Periodendauer ist ein Vielfaches der Schwingungsdauer des zugeordneten linearen Systems).

/*********************************************************/
/* declarations */
assume(g>0, u[0]>0);

/* parameter */
params: [F(t) = 2*gamma*m*g*sin(Omega*t),
         Omega=2*%pi/T[Omega],
         b = 2*D*m*omega[0],
         omega[0] = 2*%pi/T[l],
         T[Omega]=eta*T[l]];

Spring Characteristic

Die Gummi-Element Federkennlinie approximieren wir über die punktsymmetrische Funktion

$\displaystyle {\frac {K(u_{t})}{mg}}=c_{1}\cdot \left({\frac {u_{t}}{u_{0}}}\right)+c_{3}\cdot \left({\frac {u_{t}}{u_{0}}}\right)^{3}$

Kennlinie

Die beiden Konstanten c1 und c2 erhalten wir aus den Bedingungen

$\displaystyle {\frac {K(u_{0})}{mg}}=1{\text{ und }}{\frac {K(2\;u_{0})}{mg}}=3$,

die wir aus der Kennlinie ablesen zu

$\displaystyle c_{1}={\frac {5}{6}},c_{3}={\frac {1}{6}}$

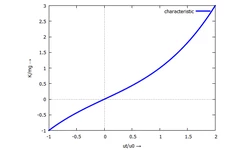
So sieht die Kennlinie dann aus:

/*********************************************************/
/*  define friction characteristics (Reib-Kennlinie) */
curve : c[1]*u[t]/u[0] + c[3]*(u[t]/u[0])^3;
sol: solve([subst([u[t]=u[0]],curve) = 1,
            subst([u[t]=2*u[0]],curve) = 3],[c[1],c[3]])[1];
curve : subst(sol,curve);
 
plot2d(subst([u[t]=mu*u[0]],curve), [mu,-1,2],
      [legend,"characteristic"],
      [style, [lines,3,1]], [xlabel, "ut/u0 →"],
      [ylabel, "K/mg →"])$

Equilibrium Conditions

Die Bewegungsgleichungen des Systems bekommen wir direkt aus dem Kräftegleichgewicht am Körper (mit dem Prinzip von d'Alembert) zu

$2\,m\;{\ddot {u}}+2\,K(u_{t})=2\,mg+F(t)$

Freikörperbild

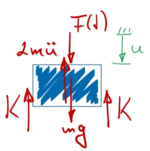
Damit die "homogene Lösung" der Bewegung (der Einschwingvorgang in die periodische Lösung) nach endlicher Zeit weg ist, mogeln wir noch etwas Dämpfung hinzu:

$2\,m\;{\ddot {u}}+{\color {red}{2\,b\,{\dot {u}}}}+2\,K(u_{t})=2\,mg+F(t)$ .

Wir brauchen auch die linearisierte Bewegungsgleichung. Dazu entwickeln wir die Federkennlinie um die stationäre Ruhelage u = u₀ des Aggregats in eine Taylor-Reihe bis zum linearen Glied, setzen also

$u=u_{0}+u_{l}(t){\text{ mit }}u_{l}\ll u_{0}$

und finden die linearisierte Form der Bewegungsgleichung zu

$\displaystyle 2\,m\cdot {\ddot {u_{l}}}+2\cdot b\cdot {\dot {u}}_{l}+{\frac {8\cdot mg}{3\cdot {{u}_{0}}}}\cdot {{u}_{l}}=\mathrm {F} \left(t\right)$.

/*********************************************************/
/* define ODE in dim'less coordinate U */
eom : 2*m*'diff(u[t],t,2) + 2*b*'diff(u[t],t,1) + 2*m*g*curve = 2*m*g+F(t);
 
 
/* static solution (F(t)=0, diff(u[t],t,2)=0) */
 
stationary: solve(subst([F(t)=0,
                  'diff(u[t],t,1)=0,
                  'diff(u[t],t,2)=0,
                   u[t]=u[S]], eom),u[S])[3];
 
linear : subst([u[t]=u[0]],
                subst(['diff(u[t],t,2)='diff(u[l],t,2),
                       'diff(u[t],t,1)='diff(u[l],t,1)], lhs(eom))) +
         subst([u[t]=u[0]],diff(lhs(eom), u[t]))*u[l] = rhs(eom);
linear : linear - 2*m*g;
 
nonlin : expand(solve(eom, 'diff(u[t],t,2)));

Dimensionless Representation

Dimensionslos machen wir die Bewegungsgleichung mit der Referenz-Auslenkung u₀ und der Periodendauer T₀ der zugeordneten linearen Bewegungsgleichung, also

• $\displaystyle u=\mu \cdot u_{0}$ und
• $\displaystyle t=\tau \cdot T_{0}$

Umschreiben der linearen und nichtlinearen Bewegungsgleichungen in dimensionslose Form liefert mit

$b=2\,D\,m\,\omega _{0},$

• die nichtlineare Form
  

$\displaystyle {\frac {d^{2}}{d\,\tau ^{2}}}\cdot \mu +4\cdot \pi \cdot D\cdot \left({\frac {d}{d\,\tau }}\cdot {\mu }\right)+{\frac {\pi ^{2}}{2}}\cdot \left(5\mu +\mu ^{3}\right)=3\cdot {{\pi }^{2}}\cdot \left(1+\gamma \,\mathrm {sin} \left({\frac {2\cdot \pi \cdot \tau }{\eta }}\right)\right)$ und

• die linearisierte Form
  

$\displaystyle {\frac {{d}^{2}}{d\,{{\tau }^{2}}}}\cdot {{\mu }_{l}}+4\,D\cdot \pi \cdot \left({\frac {d}{d\,\tau }}\cdot {{\mu }_{l}}\right)+4\cdot {{\pi }^{2}}\cdot {{\mu }_{l}}=3\cdot {{\pi }^{2}}\cdot \mathrm {sin} \left({\frac {2\cdot \pi \cdot \tau }{\eta }}\right)\cdot \gamma$.

/********************************/
/* redefine ODE in dim'less coordinate U */
dimless: ['diff(u[l],t,2)=u[0]*'diff(mu[l],tau,2)/T[l]^2,
          'diff(u[t],t,2)=u[0]*'diff(mu[n],tau,2)/T[l]^2,
          'diff(u[l],t,1)=u[0]*'diff(mu[l],tau,1)/T[l],
          'diff(u[t],t,1)=u[0]*'diff(mu[n],tau,1)/T[l],
           u[l]=mu[l]*u[0],
           u[t]=mu[n]*u[0],
           t=tau*T[l]];
 
linear : subst(dimless,subst(params,linear));
linear : linear/coeff(lhs(linear),'diff(mu[l],tau,2));
linear : expand(linear);
 
dimless : append(dimless,
           [solve(coeff(lhs(linear),mu[l]) = 4*%pi^2,T[l])[2] ]);
 
linear: subst(dimless,linear);
nonlin : expand(subst(dimless,subst(params,3*%pi^2*nonlin/g)));

Solving

Teil A: Partikulare Lösung der linearen Bewegungsgleichung

Von der linearen Bewegungsgleichung wollen wir nur die partikulare Lösung - also die Lösung nach Abklingen des Einschwingvorgangs (dafür brauchten wir die Dämpfung!). Wir wählen als Ansatz

$\displaystyle {{\mu }_{l}}(\tau )={{U}_{s}}\cdot \mathrm {sin} \left({\frac {2\cdot \pi \cdot \tau }{\eta }}\right)+{{U}_{c}}\cdot \mathrm {cos} \left({\frac {2\cdot \pi \cdot \tau }{\eta }}\right)$

(Ansatz vom Typ der rechten Seite)

und erhalten für die Koeffizienten

${\begin{array}{l}\displaystyle {{U}_{c}}=-{\frac {3\cdot {{\eta }^{3}}\cdot D\cdot \gamma }{8\cdot {{\eta }^{2}}\cdot {{D}^{2}}+2\cdot {{\eta }^{4}}-4\cdot {{\eta }^{2}}+2}},\\\displaystyle {{U}_{s}}={\frac {3\cdot {{\eta }^{4}}\cdot \gamma -3\cdot {{\eta }^{2}}\cdot \gamma }{16\cdot {{\eta }^{2}}\cdot {{D}^{2}}+4\cdot {{\eta }^{4}}-8\cdot {{\eta }^{2}}+4}}\end{array}}$.

Die Lösung plotten wir unten.

Teil B: Numerische Lösung des Anfangswertproblems

Für die numerische Lösung brauchen die Bewegungsgleichung als Differentialgleichung erster Ordnung als

${\begin{array}{ll}\displaystyle {\frac {d\,\mu }{d\,\tau }}&=\nu ,\\\displaystyle {\frac {d\,\nu }{d\,\tau }}&\displaystyle =-4\cdot \pi \cdot D\cdot \nu -{\frac {\pi ^{2}}{2}}\left(5\mu +\mu ^{3}\right)+3\pi ^{2}\left(1+\gamma \sin({\frac {2\cdot \pi \cdot t}{\eta }})\right)\end{array}}$.

Die lösen wir nun als Anfangswertproblem

${\underline {\dot {q}}}={\underline {f}}({\underline {q}})$

mit

${\underline {q}}=\left({\begin{array}{c}\mu \\\nu \end{array}}\right)$.

Als Anfangsbedingungen wählen wir die stationäre Ruhelage des Aggregats, also

${\underline {q}}_{0,1}=\left({\begin{array}{l}1\\0\end{array}}\right)$.

Und wir führen die numerische Integration mit drei Parameter-Sätzen durch:

1. Überkritische Anregung:
   $\eta =0.5,\gamma =1,D=0.1$ Hier ist η = 1/2, also erfolgt die Anregung mit einer Periodendauer, die halb so groß ist, wie die Periodendauer des linearisierten Systems - oder: die Erregerfrequenz ist doppelt so hoch wie die Eigenfreuqenz.
2. Anregung in der Nähe der Resonanzfrequenz:
   $\eta =1.1,\gamma =1,D=0.1$ Mit η = 1.1 regen wir in der Nähe der Erregerfrequenz des linearen Systems an - etwas darunter, die Phase des Systems ist also fast noch konphas mit der Erregung.
3. Unterkritische Anregung:
   $\eta =2.0,\gamma =1,D=0.1$Hier ist Erregerfrequenz nur hald so groß, wie die Eigenfrequenz des linearen Systems, die Phase des Systems ist also konphas zur Erregung.

/***********************************************/
/* inhomogenous part of linearized solution */
ansatz: [mu[l] = U[c]*cos((2*%pi*tau)/eta)+U[s]*sin((2*%pi*tau)/eta)];
linSol: subst(ansatz,linear);
linSol: expand(ev(linSol,nouns));
linSol: solve([coeff(linSol,cos((2*%pi*tau)/eta)),
               coeff(linSol,sin((2*%pi*tau)/eta))],[U[c],U[s]])[1];

numpar: [[eta=0.5,gamma=1, D=0.1],
         [eta=1.1,gamma=1, D=0.1],
         [eta=2.0,gamma=1, D=0.1]];
/* plot results, time domain  */
for i: 1 thru length(numpar) do
    plot2d(subst(numpar[i],subst(linSol, subst(ansatz,mu[l]))),[tau,0,2],
           [xlabel, "τ ->"], [ylabel, "μ ->"], [legend, sconcat("@: ",string(numpar[i]))]);
 
/********************************/
/* numerical solution of IVP */
         
times : subst([t0 = 0, tmax = 20, dt = 0.001],
                    [t, t0, tmax, dt]);
 
dgl1stOrder : [V, 
subst(solve(nonlin, 'diff(mu[n],tau,2)),'diff(mu[n],tau,2))];
dgl1stOrder : subst(['diff(mu[n],tau,1)=V,mu[n]=U, tau=t],dgl1stOrder);
 
stateVabs : [U,V];
initiVals : [1,0];
 
/* solution of IVP (ivs) */
for i: 1 thru length(numpar) do
    ivs[i] : rk(subst(numpar[i], dgl1stOrder), stateVabs, initiVals, times)$

Post-Processing

Für die dreiAnfangsbedingungen erhalten wir die Auslenkungen U(τ):

#	Auslenkung	Geschwindigkeit
1)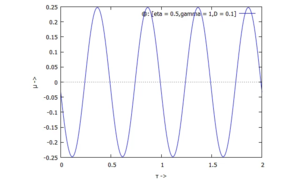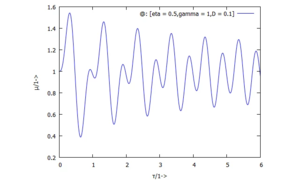
2)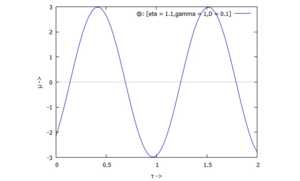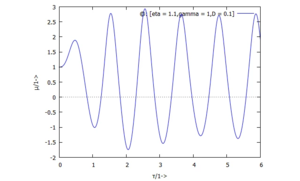
3)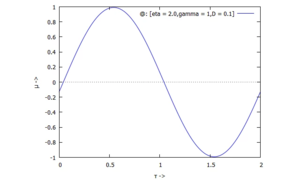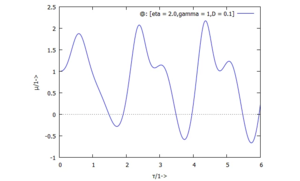

Für das nichtlineare System können wir uns den Einschwingvorgang im Phasendiagramm ansehen:

Phasendiagramme

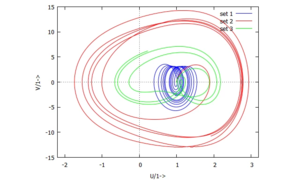
Und stellen fest:

• nur für die überkritische Lösung ist die Auslenkungen des Systems so klein, dass eine Linearisierung gerechtfertigt ist.

Für die Parameter-Sätze 3 und besonders 2 entstehen Schwingungen mit hohen Amplituden, die wir in jedem Fall als nichtlineares Problem lösen müssen.

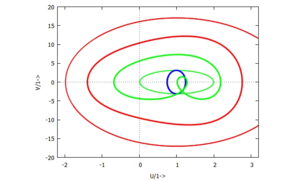
Und im eingeschwungenen Zustand können wir die Lösung für lineares und nichtlineares System einfach vergleichen. Die Lösungen des linearen Systems sind immer Ellipsen, die Lösungen des nichtlinearen Systems sind deutlich "kunstvoller":

/********************************/
/* plot results, time domain  */
for i: 1 thru length(numpar) do
    (T[i] : makelist(ivs[i][j][1],j,1,length(ivs[i])),
     uD[i] : makelist(ivs[i][j][2],j,1,length(ivs[i])),
     vD[i] : makelist(ivs[i][j][3],j,1,length(ivs[i])),
     plot2d([discrete, T[i], uD[i]],
          [legend, sconcat("@: ",string(numpar[i]))],
                       [xlabel,"τ/1->"], [ylabel,"μ/1->"]));
 
/* phase plot */
curves : makelist([discrete,uD[i],vD[i]],i,1,length(numpar))$
plot2d(curves, [legend, false], [x,-2.2,3.2],
                   [ylabel,"V/1->"], [xlabel,"U/1->"]);

/********************************/
/* phase plot - linear and nonlinear  */
curves : makelist(subst(numpar[i],subst([tau=t],subst(linSol,subst(ansatz,[parametric, 1+mu[l], 'diff(mu[l],tau),[t,0,2]])))),i,1,length(numpar));
curves : ev(curves,nouns);

/* get last 2 "seconds" of numerical solution */
for i: 1 thru length(numpar) do
     (uDL[i] : makelist(uD[i][j],j,length(uD[i])-round(2/times[4]),length(uD[i])),
      vDL[i] : makelist(vD[i][j],j,length(vD[i])-round(2/times[4]),length(vD[i])));

curves : append(curves,makelist([discrete,uDL[i],vDL[i]],i,1,length(numpar)))$

plot2d(curves, [legend, false], [x,-2.2,3.2],
       [style, [lines,2,1], [lines,2,2], [lines,2,3], [lines,3,1], [lines,3,2], [lines,3,3]],
                   [ylabel,"V/1->"], [xlabel,"U/1->"]);

🧨 Unzulässige Belastung von Gummifedern:

Das Phasendiagramm zeigt: die Gummifeder wird für die Parameter-Sets 2 und 3 deutlich auf Zug belastet  - das ist nicht zulässig!

---

Links

• ...

Literature

• ...