Gelöste Aufgaben/Kit5

Aufgabenstellung

Bei diesem Randwertproblem wird ein Euler-Bernoulli-Balken (Elastizitätsmodul E, Flächenmoment 2-ten Grades I) mit einer Streckenlast q₀ im Bereich A-B belastet. In A  ist der Balken fest eingespannt, wobei durch eine Einbau-Ungenauigkeit der Rand im Verhältnis 1:10 geneigt ist.

In B hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen.

Datei:Kit5.png.png

Lageplan

Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist.

Lösung mit Maxima

In Kit4 finden Sie die Transformation der Bewegungsgleichung des Euler-Bernoulli-Balkens in die dimensionslose Form mit der allgemeinen Lösung

${\tilde{w}}_i\left(\xi \right):=\frac{\mu \cdot {\xi }^4}{24}+\frac{C_{i,3}\cdot {\xi }^3}{6}+\frac{C_{i,2}\cdot {\xi }^2}{2}+C_{i,1}\cdot \xi +C_{i,0}$

für die Bereiche i=1 (A-B) und i=2 (B-C).

Koordinaten

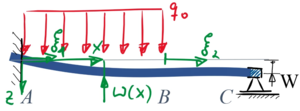
Dazu gehören die neuen dimensionslose Koordinaten ξ₁ und ξ₂:

Die Rand- und Übergangsbedingungen lauten dann mit ℓ₂ = ℓ₁/2

$\begin{array}{ccl}{\tilde{w}}_1(0)& =& 0\\ \tilde{w}{\text{'}}_1(0)& =& 1/10\end{array}$, $\begin{array}{ccl}{\tilde{w}}_1(1)& =& {\tilde{w}}_2(0)\\ \tilde{w}{\text{'}}_1(1)& =& \tilde{w}{\text{'}}_2(0)\\ {\tilde{w}}^{\prime }{\text{'}}_1(1)& =& {\tilde{w}}^{\prime }{\text{'}}_2(0)\\ {\tilde{w}}^{″}{\text{'}}_1(1)& =& {\tilde{w}}^{″}{\text{'}}_2(0)\end{array}$, $\begin{array}{ccl}{\tilde{w}}_1(1/2)& =& W\\ \tilde{w}{\text{'}}_2(1/2)& =& 0\end{array}$

Lösen der dimensionslosen Bewegungsgleichung

Damit es einfacher wird, lassen Tilde über w weg. Die Bewegungsgleichung für beide Bereiche ist dann

$w^{⁗}(\xi )=\mu$

und deren allgemeine Lösung

$\begin{array}{l}{w}_1\left(\xi \right):=\frac{\mu \cdot {\xi }^4}{24}+\frac{C_{1,3}\cdot {\xi }^3}{6}+\frac{C_{1,2}\cdot {\xi }^2}{2}+C_{1,1}\cdot \xi +C_{1,0}\\ w_2\left(\xi \right):=\frac{C_{2,3}\cdot {\xi }^3}{6}+\frac{C_{2,2}\cdot {\xi }^2}{2}+C_{2,1}\cdot \xi +C_{2,0}\text{ (hier ist }\mu =0)\end{array}$

/* solve dim'less dgl (see "Dimensionen und Einheiten") ....*/
dgl : diff(w(xi),xi,4) = mu;
/* generic solution */
displ : expand(solve(integrate(
						integrate(
							integrate(
								integrate(dgl,xi),xi),
											  xi),
												xi), w(xi)));												
/* adapt to section 1 (AB) und section 2 (BC) */
sections: [[i=1,
			%c4=C[1,0], %c3=C[1,1], %c2=C[1,2], %c1=C[1,3]],
           [i=2, 
			%c4=C[2,0], %c3=C[2,1], %c2=C[2,2], %c1=C[2,3],
			mu = 0]];

/* section  I */
define(  w[1](xi),  subst(sections[1],subst(displ,w(xi))));
/* section II */
define(  w[2](xi),  subst(sections[2],subst(displ,w(xi))));

Formulation of Boundary Conditions

Einsetzten der Lösung der Bewegungsgleichungen in die Randbedingungen liefert die Gleichungen

$\left(\begin{array}{c}{C}_{1,0}=0\\ C_{1,1}=\frac{1}{10}\\ \frac{\mu }{24}+\frac{C_{1,3}}{6}+\frac{C_{1,2}}{2}+C_{1,1}+C_{1,0}=C_{2,0}\\ \frac{\mu }{6}+\frac{C_{1,3}}{2}+C_{1,2}+C_{1,1}=C_{2,1}\\ \frac{\mu }{2}+C_{1,3}+C_{1,2}=C_{2,2}\\ \mu +C_{1,3}=C_{2,3}\\ \frac{C_{2,3}}{8}+\frac{C_{2,2}}{2}+C_{2,1}=0\\ \frac{C_{2,3}}{48}+\frac{C_{2,2}}{8}+\frac{C_{2,1}}{2}+C_{2,0}=1\end{array}\right)$

mit den Unbekannten

$\underset{\_}{x}=\left(\begin{array}{c}{C}_{1,0}\\ C_{1,1}\\ C_{1,2}\\ C_{1,3}\\ C_{2,0}\\ C_{2,1}\\ C_{2,2}\\ C_{2,3}\end{array}\right)$.

/* formulation of boundary conditions */
bc : flatten(
     [w[1](0) = 0,
      subst([xi=0],diff(w[1](xi),xi))=1/10,
	  makelist(subst([xi=1],diff(w[1](xi),xi,j))
             =subst([xi=0],diff(w[2](xi),xi,j)),j,0,3),
	  subst([xi=1/2],diff(w[2](xi),xi))=0,
	  w[2](1/2) = 1]);
/* and unknowns*/
ic : flatten(makelist(makelist(C[i,j],j,0,3),i,1,2));

The Equations of Motion

Das Gleichungssystem

$\underset{\_}{\underset{\_}{A}}\cdot \underset{\_}{x}=\underset{\_}{b}$

hat dabei die Koeffizientenmatrix

$\underset{\_}{\underset{\_}{A}}=\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 1& 1& \frac{1}{2}& \frac{1}{6}& -1& 0& 0& 0\\ 0& 1& 1& \frac{1}{2}& 0& -1& 0& 0\\ 0& 0& 1& 1& 0& 0& -1& 0\\ 0& 0& 0& 1& 0& 0& 0& -1\\ 0& 0& 0& 0& 0& 1& \frac{1}{2}& \frac{1}{8}\\ 0& 0& 0& 0& 1& \frac{1}{2}& \frac{1}{8}& \frac{1}{48}\end{array}\right)$

sowie die rechte Seite

$\underset{\_}{b}=\left(\begin{array}{c}0\\ \frac{1}{10}\\ -\frac{\mu }{24}\\ -\frac{\mu }{6}\\ -\frac{\mu }{2}\\ -\mu \\ 0\\ 1\end{array}\right)$

/* Linear Equations of Motion */
ACM : augcoefmatrix(bc,ic);
A : submatrix(ACM,9);
b : -col(ACM,9);

Solving

Wir erhalten

$[C_{1,0}=0,C_{1,1}=\frac{1}{10},C_{1,2}=\frac{72+5\cdot \mu }{30},C_{1,3}=-\frac{444+95\cdot \mu }{135},C_{2,0}=\frac{2436+25\cdot \mu }{3240},C_{2,1}=-\frac{5\cdot \mu -231}{270},C_{2,2}=-\frac{24+\mu }{27},C_{2,3}=\frac{40\cdot \mu -444}{135}]$.

/* solve .... */
sol[1] : solve(bc,ic);

Post-Processing

w(x)

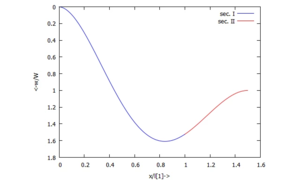
Die Lösung plotten wir, z.B. für die Streckenlast μ=100:

Die dimensionslose Auslenkung ist jetzt etwas größer als "1" - Sie müssen sich also jetzt überlegen, ob Ihre Theorie noch gültig ist!

/* for plotting, use mu=100 */
params: [mu=100];
sol[2] : expand(
      subst(params,subst(sol[1],[w[1](xi),w[2](xi)])));
/* coordinate-transformation put the functions back "in place"*/
plot2d ([[parametric, t, subst(t,xi,sol[2][1]), [t,0,1]],
         [parametric, 1+t, subst(t,xi,sol[2][2]), [t,0,1/2]]],
         [gnuplot_preamble, "set yrange [] reverse"],
         [legend, "sec. I", "sec. II"], 
         [xlabel, "x/l[1]->"], [ylabel, "<-w/W"]);

---

Links

• ...

Literature

• ...