Gelöste Aufgaben/JUMP/Car-Body
Scope
In common simulation applications - especially for full-size commercial cars - the pitch-angle of the car is assumed to be small to allow for a linearization of geometry and most parts of the equations of motion. We drop this limitation so we can do more fancy stuff with our model - like climbing steep roads or jumping across ditches.
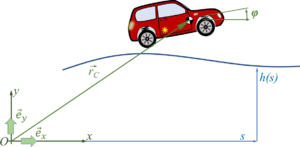
We employ a spatial x-y coordinate system, x in horizontal, y in vertical, upwards direction. And we’ll briefly employ the z-axis as rotation direction - which is towards you following the “right-hand-rule“ for coordinate systems.
Structure
The driver controls the car's motion via the position of the "gas"-pedal, which is being translated into a torque MW at the wheel.
This toque will change velocities and thus the position of the car. These state-variables will then create - via info - a feedback to the driver.
We’ll need to invest significant efforts in describing the kinematics of the car-motion and to derive its equations of body-motion since we do not want to limit our study on small pitch-angles of the car. Key accessory will be vectors, which map locations like the center of mass:
- .
This vector has - in 2D - two coordinates , measured in the inertial x-y frame:
- with .
representing the unit vectors spanning the x-y space. If we refer to a specific frame, we may drop the vector-notation and refer to the column-matrix of coordinates only, so
- .
We’ll also employ coordinate transformations using Euler-rotations.
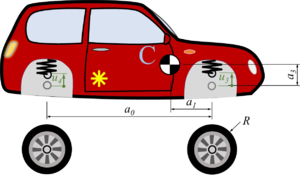
The car with front-wheel drive consists of the car-body with center of mass “C“, the front wheels “A“ and the rear wheel “B“. Masses of car-body and wheel-sets are M and m respectively.The geometry of the car is described by
- a0: the wheel base;
- a1: longitudinal distance between center of mass and front-wheel-hub;
- a2 = a0 - a1 and
- a3: vertical distance between center of mass and front-wheel-hub (relaxed springs).
tmp
Body
We use five coordinates to describe the motion of the car:
- for the location of the center of mass of the car-body and its pitch-angle
 ,
, - for the "vertical" motion of the wheel hubs relative to the car-body - which is synonym to the compression of the springs
and - as the rotation angle of the front-wheel - we'll not account for the rotation of the rear-wheel.
So the center of mass of the car-body is
- ,
the coordinate system of the car is
where
- .
So the location of the front-wheel “A“ is
or
- .
Likewise, the location of the rear-wheel “B“ is
and in the following, we’ll be using the abbreviations
and
- .
tmp
Track
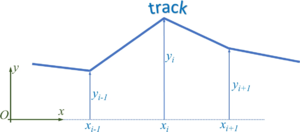
We describe the road by road-sections, which we call tracks. We start by defining each track as a line-segment, i.e. a first-order polynomial. The road is thus defined by pairs of track-endpoints, i.e. (xi, yi).
The track-polynomials are
- .
During the numerical integration of the initial-value-problem - when the car runs along the track - the solver needs to cope with the transition between two straight lines - which is numerically more efficient if we convert the road in a continuously differentiable function.
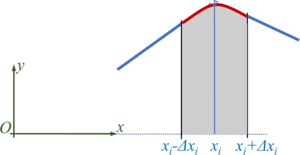
For this purpose, we define transition polynomials pi of second degree - parabolas - as
which connect two neighboring tracks.
The boundary conditions for the parabolas (red) and the neighboring lines (blue) yield
And though we have four boundary conditions, they allow for a solution with three unknown polynomial coefficients Pi if Δxi is identical left and right from xi - which we have already implied.
and
But instead of employing the above, we solve the linear systems of equations for the coefficients numerically.
Now each polynomial creates new endpoints xi - Δxi and xi + Δxi which substitute for the initial xi-point. The tracks are represented by a succession of lines and parabolas.
Next we need to find the contact point between wheel and road!
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2021-02-08 */
/* ref: Modelling and Simulation (TUAS) */
/* description: Rounding between straight line-segments*/
/*******************************************************/
/*******************************************************/
/* declarations */
/*******************************************************/
declare("Δ",alphabetic);
params: [x[0] = 0, x[1] = 10, x[2]=15,
y[0] = 0, y[1] = 1, y[2]=-1,
eps = 0.2];
/*******************************************************/
/* polynomials */
/*******************************************************/
/* polynomial coefficiets of two consecutive straigt lines */
P : [[a[1,1],a[1,0]],[a[2,1],a[2,0]]];
/* polynomials of cubic and two consecutive linear polynomials */
p : [a[1,1]*x+a[1,0],
b[3]*x^3+b[2]*x^2+b[1]*x+b[0],
a[2,1]*x+a[2,0]];
/* compute polynomial coefficients from (x[i]/y[i])-points*/
linear : solve([subst([x=x[0]],p[1]) = y[0],
subst([x=x[1]],p[1]) = y[1],
subst([x=x[1]],p[3]) = y[1],
subst([x=x[2]],p[3]) = y[2]], [a[1,0],a[1,1],a[2,0],a[2,1]])[1];
/* equations to continuously fit cubic function to lines */
equs : [subst([x=x[1]-Δx], p[1]) = subst([x=x[1]-Δx], p[2]),
subst([x=x[1]+Δx], p[3]) = subst([x=x[1]+Δx], p[2]),
subst([x=x[1]-Δx], diff(p[1],x)) = subst([x=x[1]-Δx], diff(p[2],x)),
subst([x=x[1]+Δx], diff(p[3],x)) = subst([x=x[1]+Δx], diff(p[2],x))];
/* unknowns */
Q : [b[3],b[2],b[1],b[0]];
/* solve for unknowns */
sol : ratsimp(subst(linear,solve(equs,Q)[1]));
/* solve linear system of equations for unknown coefficients */
ACM : augcoefmatrix(equs,Q);
print(submatrix(ACM,5)," * ",transpose(Q)," = ",col(ACM,5))$
/* or - more simple when doing it numerically .... */
/* coefficients of straigt line polynomials */
s : makelist(a[i,1] = (y[i-1]-y[i])/(x[i-1]-x[i]),i,1,2);
P : [[a[1,1],a[1,0]],[a[2,1],a[2,0]]];
p : [a[1,1]*x+a[1,0],
b[3]*x^3+b[2]*x^2+b[1]*x+b[0],
a[2,1]*x+a[2,0]];
linear : solve([subst([x=x[1]],p[1]) = y[1],
subst([x=x[1]],p[3]) = y[1]], [a[1,0],a[2,0]])[1];
equs : [subst([x=x[1]-Δx], p[1]) = subst([x=x[1]-Δx], p[2]),
subst([x=x[1]+Δx], p[3]) = subst([x=x[1]+Δx], p[2]),
subst([x=x[1]-Δx], diff(p[1],x)) = subst([x=x[1]-Δx], diff(p[2],x)),
subst([x=x[1]+Δx], diff(p[3],x)) = subst([x=x[1]+Δx], diff(p[2],x))];
Q : [b[3],b[2],b[1],b[0]];
sol : ratsimp(subst(linear,solve(equs,Q)))[1];
/* check with parameters */
subst(params,subst(s,subst(linear,solve(equs,Q))));
tmp
Contact-Point and -Normal
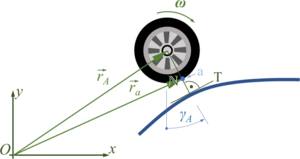
Finding the contact between wheel and road is our next challenge. We need to differentiate between the straight lines and the parabolas - but in both cases, we are looking for the equation of the normal “N“ to the road-surface, which cuts through the wheel-hub.
From the car-coordinates, we know the location of the wheel - e.g. “A” - expressed by its hub-vector
- .
And we can also define
- .
where is the vector to the contact point “a“ of wheel “A“ and is the vector from “a“ to the wheel hub “A“. Since "a" is a point on a track - if wheel and road have contact - and the direction of NA is known to be perpendicular to this track in “a”, we have two equations for the two unknowns “point on track“ and “length of normal “.
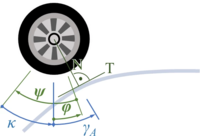
However, it remains tricky to find the material coordinate of the wheel that is at “a“. The picture below explains how first rotate the car by φ - positive about the z-axis, then rotate the wheel in negative direction by ψ and by κ in positive direction back to vertical. From there it is the known angle γA to “a“.
This succession of rotations is expressed by
and we find contact point “a“ from
and “b“ from
- .
For wheel A und B, the angles ψ and κ are not identical - but we have dropped the indices here for brevity.
Track is a Line
If the track is line “i“, we have
with
being start- end end-points of the line with coordinates [xi, hi] and ξ naming the coordinate of point “C“. For the track-normal, we have
with the unit-normal , the wheel-radius R and the unknown η. For the unit-normal
holds.
And for the contact angles γA/B we employ
- .
Track is a Parabola
If the track is defined by a second-order polynomial pi, we proceed accordingly. However, the track inclination is linearly dependent on “x” and we find that the normal is proportional to:
From
we get two equations for the unknowns “x“ and “η“ as
- .
And we get a third-degree polynomial in “x“ from the second equation. The three solutions for point “C” usually comprise complex (they have a real and imaginary part) solutions depending on the curvature (convex or concave) of the parabola. That’s not a problem but increases computational cost significantly - because we will need to solve this equation for each value of U3, U4 again and again.
tmp
Contact Forces
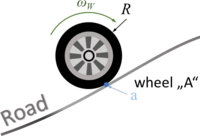
At contact “a” between road and wheel, the motor-torque must be transformed into a propulsion force of the car.
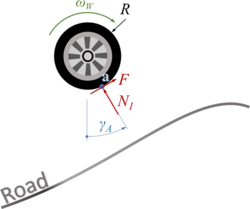
In the freebody-diagram for wheel “A“ below, we account for the contact forces
- normal force Na and
- traction force F.
The interaction between road and wheel is a complex relationship between these two forces and the relative velocity vrel of the wheel in point C relative to the road.
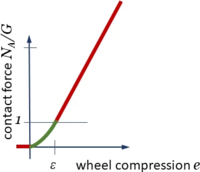
For the normal force NA we assume a characteristic which depends on the dimensionless compression of the wheel e = 1-η, where - obviously -
To have a continuously differentiable function NA as in this contact-characteristic, we choose a parabola for 0<e<ε with continuous transitions to
And - for the sake of simplicity - let
- .
Now, for the traction force, we assume
and introduce a point-symmetric characteristic for this relationship μ(vrel):
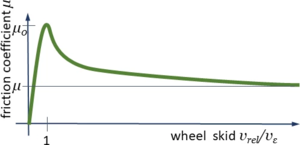
It mimics the key properties of dry friction with a stick-coefficient μ0 for very low relative velocities and μ else. To simplify implementation, we’ll be using the same mechanism as for the tracks to compose this characteristic from lines and transition parabolas.
1+1=2
tmp
Track
Text
1+1=2
tmp
Contact Forces
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
Variables
Parameter
x
y
z
a
b
c
next workpackage: driver-controls →
References
- ...