Gelöste Aufgaben/DGEB: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 3: | Zeile 3: | ||
[[Category:Stab]] | [[Category:Stab]] | ||
[[Category:Prinzip_der_virtuellen_Verrückungen]] | [[Category:Prinzip_der_virtuellen_Verrückungen]] | ||
[[Koordinaten]] | |||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
In dieser Aufgabe starten wir von "first principles" - hier das [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] - und entwicklen die Bewegungsgleichunge für einen schlanken Stab unter Langskräft und Biegemoment. | In dieser Aufgabe starten wir von "first principles" - hier das [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] - und entwicklen die Bewegungsgleichunge für einen schlanken Stab unter Langskräft und Biegemoment. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:DGEB-01.png|links|mini|Lageplan.]] | [[Datei:DGEB-01.png|links|mini|Lageplan.]] | ||
Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie ''δΠ''. | Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab mit Rechteck-Querschnitt unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie ''δΠ''. | ||
Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens. | Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens. | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit | ==Lösung mit Maxima== | ||
Wie alle zentralen Begriffe der Elastizitätstheorie ineinandergreifen, um die virtuelle Formänderungsenergie für den Euler-Bernoulli-Balken zu ermitteln, zeigt diese Aufgabe. | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Hier kommen | |||
* das [[Sources/Lexikon/Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation)|Hook'sche Gesetz]] in seiner allgemeinen, 3D-Fassung, | |||
* die allgemeinen [[Sources/Lexikon/Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)|Verschiebungs-Verzerrungs-Bedingungen]], | |||
* die klassischen Annahmen zur Theorie von Stäben zum Einsatz sowie | |||
* die Gleichgewichtsbedingungen nach dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]]. | |||
zum Einsatz. | |||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="maxima" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2016-03-27 */ | |||
/* ref: Euler-Bernoulli Beam */ | |||
/* description: derives the equations of motion for */ | |||
/* the Timoshenko and EBB beam */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 26: | Zeile 42: | ||
|text=Text | |text=Text | ||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | 1+1 | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Zeile 34: | Zeile 50: | ||
|text=Text | |text=Text | ||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="maxima" line start=1> | ||
1+1 | 1+1 | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Zeile 82: | Zeile 98: | ||
'''Links''' | '''Links''' | ||
* ... | *... | ||
'''Literature''' | '''Literature''' | ||
* ... | *... | ||
Version vom 23. Februar 2021, 09:42 Uhr
Aufgabenstellung
In dieser Aufgabe starten wir von "first principles" - hier das Prinzip der virtuellen Verrückungen - und entwicklen die Bewegungsgleichunge für einen schlanken Stab unter Langskräft und Biegemoment.
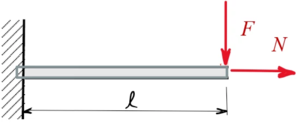
Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab mit Rechteck-Querschnitt unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie δΠ.
Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens.
Lösung mit Maxima
Wie alle zentralen Begriffe der Elastizitätstheorie ineinandergreifen, um die virtuelle Formänderungsenergie für den Euler-Bernoulli-Balken zu ermitteln, zeigt diese Aufgabe.
Header
Hier kommen
- das Hook'sche Gesetz in seiner allgemeinen, 3D-Fassung,
- die allgemeinen Verschiebungs-Verzerrungs-Bedingungen,
- die klassischen Annahmen zur Theorie von Stäben zum Einsatz sowie
- die Gleichgewichtsbedingungen nach dem Prinzip der virtuellen Verrückungen.
zum Einsatz.
Declarations
Text
Euler Rotation
Text
Stress-Strain-Relations for a Rod
Text
Displacement Variables
Text
Virtual Strain Energy
Text
Timoshenko-Beam
Text
Euler-Bernoulli-Balken
Text
Links
- ...
Literature
- ...