Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Integration der Differentialbeziehung (IVP)

Was ohen Computer geht ...

Ohne Computer interessieren uns meist nur Anfangswertprobleme, bei denen wir eine analytische Lösung des Anfangswertproblems angeben können.

Integration der Bewegungsgleichung

Die Bewegungsdifferentialgleichung eines Körpers im Erdschwerefeld sei - ohne Einflüsse der Luft - für die Koordinaten Wurf-Weite w und Wurf-Höhe h:

Diese Differentialgleichung können wir - wie auch die Biegedifferentialgleichung des Euler-Bernoulli-Balkens - integrieren, und finden

mit den Integrationskonstanten c_h1, c_h0, c_w1, c_w0.

Die Integrationsbedingungen können wir an "Randbedingungen" zu Zeitpunkten t₁, t₂ anpassen, meist aber interessiert uns die Lösung, wenn der Anfangszustand für vollständig durch Anfangsweg und Anfangsgeschwindigkeit beschrieben ist.

Die Lösungen sehen dann so aus:

Wurfparabel

Weg-Zeit-Diagramm

Geschwindigkeits-Zeit-Diagramm.

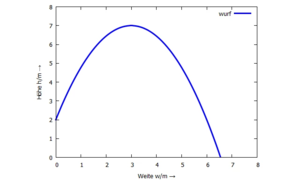
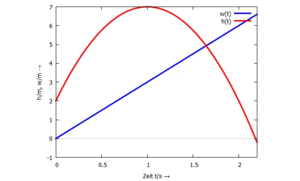
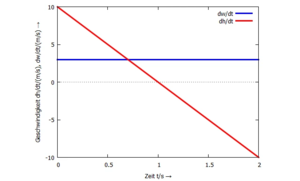
Diese Lösungsvariante spielt in Ingenieursproblemen praktisch keine Rolle, weil die Bewegungsgleichungen sich nicht geschlossen integrieren lassen.

Der e^λt-Ansatz

Meist sind die Zustandsgrößen (Auslenkung, Geschwindigkeit) der Körper unseres Systems elastisch miteinander oder an eine Umgebung gekoppelt, die Koordinaten u kommen dann in der Bewegungsgleichungen in verschiedenen Zeitableitungen (Geschwindigkeit, Beschleunigung) vor. Dann sehen die Bewegungsgleichungen so aus:

$\underset{\_}{\underset{\_}{M}}\cdot \underset{\_}{\ddot{u}}+\underset{\_}{\underset{\_}{K}}\cdot \underset{\_}{u}=\underset{\_}{f}$

mit

$\begin{array}{ll}\underset{\_}{u}& :\text{ Koordinaten des Systems}\\ \underset{\_}{\underset{\_}{M}}& :\text{ Massenmatrix}\\ \underset{\_}{\underset{\_}{K}}& :\text{ Steifigkeitsmatrix und}\\ \underset{\_}{f}& :\text{ eingeprägte Lasten auf das System}\end{array}$

.

Für diese Systeme interessiert uns sehr oft nur die homogene Lösung (f=0). Für dieses System können wir die Lösung mit den Ansatz

ansetzen (erraten). Dieser Ansatz führt auf ein Eigenwertproblem mit den Eigenwerten λ und den Eigenvektoren u.

Das schauen wir uns an dem schwingungsfähige System links an. Es besteht aus zwei Körper der Masse m sowie Federn der Steifigkeit k1=3/2 k und k2=k. Gesucht ist die Schwingung des Systems in Zeitbereich, wenn die untere Masse durch einen Schlag eine Anfangsgeschwindigkeit erfährt.