Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 154: | Zeile 154: | ||
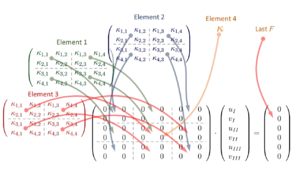
Die Element-Steifigkeits-Matrizen ''k<sub>i</sub>'' addieren wir nun je Element zur System-Steifigkeitsmatrix ''K'' hinzu - so, wie im Prozess-Schema beschrieben: | Die Element-Steifigkeits-Matrizen ''k<sub>i</sub>'' addieren wir nun je Element zur System-Steifigkeitsmatrix ''K'' hinzu - so, wie im Prozess-Schema beschrieben: | ||
[[Datei:FiniteElementeMethode-KompositionDerSteifigkeitsmatrix.png|left|mini|Komposition der Steifigkeitsmatrix.]]<br clear="all"/> | |||
Element 4 - die Feder mit der Steifigkeit ''k = κ* EA/ℓ'' addieren wir als letztes zu Element ''K''<sub>44</sub> hinzu. | Element 4 - die Feder mit der Steifigkeit ''k = κ* EA/ℓ'' addieren wir als letztes zu Element ''K''<sub>44</sub> hinzu. | ||
| Zeile 300: | Zeile 301: | ||
Für einen geraden Stab sieht eine Diskretisierung - hier mit gleich langen - Finiten Elementen so aus: | Für einen geraden Stab sieht eine Diskretisierung - hier mit gleich langen - Finiten Elementen so aus: | ||
[[Datei:FiniteElementeMethode-Stabmodelle.png|mini|Knoten und Elemente für Stabmodelle.]]<br clear="all"/> | [[Datei:FiniteElementeMethode-Stabmodelle.png|left|mini|Knoten und Elemente für Stabmodelle.]]<br clear="all"/> | ||
Der Ansatz - hier für einen [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] - ist wieder allgemein | Der Ansatz - hier für einen [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] - ist wieder allgemein | ||
| Zeile 317: | Zeile 318: | ||
Bei [[Sources/Lexikon/Schale|Schalen-Modellen]] für ebene Strukturen müssen wir Verschiebungen und/oder Verdrehungen als Funktion von zwei unabhängigen Variablen - z.B. ''x'' und ''y'' - ausdrücken. | Bei [[Sources/Lexikon/Schale|Schalen-Modellen]] für ebene Strukturen müssen wir Verschiebungen und/oder Verdrehungen als Funktion von zwei unabhängigen Variablen - z.B. ''x'' und ''y'' - ausdrücken. | ||
[[Datei:FiniteElementeMethode- | [[Datei:FiniteElementeMethode-Plattenmodelle.png|left|mini|Plattenmodell]]<br clear="all"/> | ||
Als Ansatz für eine ebene Scheibe sind die Verschiebungen in der der Schalen-Ebene in die beiden Raumrichtungen | Als Ansatz für eine ebene Scheibe sind die Verschiebungen in der der Schalen-Ebene in die beiden Raumrichtungen | ||
| Zeile 402: | Zeile 403: | ||
{{Kategorie:Finite-Elemente-Methode}} | {{Kategorie:Finite-Elemente-Methode}} | ||
Version vom 22. Februar 2021, 07:48 Uhr
Die Methode der Finiten Elemente ist deshalb so erfolgreich, weil Sie ideal mit der Implementierung im Computer harmoniert.
Auf zwei Ansätzen basiert dieser Erfolg:
Einführungsbeispiel
Wie das geht, zeige ich Ihnen - zuerst ohne Theorie - für ein Beispiel:
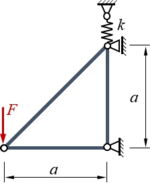
Ein Stabwerk aus drei elastischen Stäben und einer Feder wird durch eine Einzelkraft F belastet. Alle Stäbe haben die Dehnsteifigkeit EA, die Federsteifigkeit ist k.
Gegeben sind a, EA, k, F, gesucht sind die Verschiebungen der Knotenpunkte.
Die Lösung mit der Methode der Finiten Elemente zeige ich Ihnen aus drei Perspektiven:
- das Prozess-Schema
- die Lehrbuch-Sichweise und
- die Implementierung in einem Algorithmus (hier Maxima).
Das Modell für ein lineares Modell mit Finiten Elemente ist ein System linearer Gleichungen. In jeder Spalte steht die Gleichgewichtsbedingung für eine Koordinate Qi, in den Spalten stehen die Koeffizienten der Koordinaten Qj. Das Gleichungssystem sieht immer so aus:
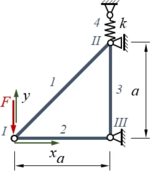
Wir benennen Stäbe und Knoten, ein Koordinatensystem brauchen wir auch:
Das Stabwerk besteht aus vier elastischen Bauteilen:
- den Stäben 1,2 und 3 sowie
- der Feder.
Und jedes dieser elastischen Bauteil hinterlässt eine Spur in der Steifigkeitsmatrix K.
Die Verformung der Stäbe erfassen wir durch die Verschiebung der Endpunkte - der Knoten - des Stabwerks. Wie das geht und wir wir daraus eine Element-Steifigkeitsmatrix für einen Dehnstab bekommen, steht in T312. Die Knoten-Verschiebungen schreiben wir in Q hinein, hier für drei Knoten die Verschiebungen jeweils u in x- und v in y-Richtung
A. Das Prozess-Schema
Das Gesamt-Gleichungssystem komponieren wir, indem die Element-Steifigkeitsmatrizen je Bauteil nach einem festen Schema in K hineinkopiert werden:
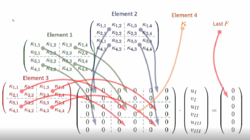
Es bleibt noch, die Randbedingungen in das System einzuarbeiten: das machen wir durch Streichen der Zeilen und Spalten des Gleichungssystems, die zu Koordinaten gehören, die aufgrund der Lagerung des Systems behindert sind:
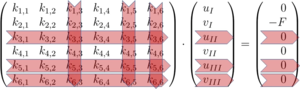
Wie dieser Prozess in einem "Lehrbuch" der Mechanik / Mathematik und in einer Implementierung im Computer aussieht folgt hier in der linken bzw. rechten Spalte:
B: Die Lehrbuch-Sichtweise |
C: Die Implementierung in MAXIMA |
Header
Für diese Aufgabe nutzen wir Ergenisse aus T312.
In diesem Beispiel sind die gesuchten Größen die Verschiebungen der drei Knoten in x- und y-Richtung, also:
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-05-30 */
/* ref: FEM */
/* description: Berechnung der Knoten-Verscheibungen */
/* eines elastischen Stabwerks */
/* - gehört zu Aufgabe T312 */
/*******************************************************/
/* coordiates in K*Q=P */
Q: transpose(matrix(flatten(makelist([u[i],v[i]],i,1,length(N)))));
System Parameter
Die Knoten (Nodes) I, II und III des Fachwerks haben die Koordinaten [xi, yi]:
Jeder Stab (Rod) ist ein Finites Element des Fachwerks, die drei Stabe verbinden folgende Knoten miteinander:
Damit berechnen wir die Parameter [ξx, ξx] aus T312
- ,
die wir für den nächsten Schritt brauchen:
/* parameters */
assume(a>0);
/* nodal coordinates */
N : [[0, 0],
[a, a],
[a, 0]];
/* rod-connectivity */
R : [[1,2],
[1,3],
[2,3]];
dims: [length(N),length(R)];
/* compute elements of Element-Stiffness Matrix */
/* Δx / Δy */
d : makelist(N[R[i][2]]-N[R[i][1]],i,1,length(R));
/* reference-lengths */
l : makelist(sqrt(d[i].d[i]),i,1,length(d));
/* normalized Δx / Δy ( xi )*/
xi : makelist((N[R[i][2]]-N[R[i][1]])/l[i],
i,1,length(R));
Definition of the Element Stiffness-Matrix
Die Element-Steifigkeitsmatrix aus T312 sieht so aus:
- Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle k\left(EA,\ell,\xi\right) := \displaystyle \frac{EA}{\ell} \cdot \begin{pmatrix} {{\xi}_x^{2}} & {{\xi}_x}\cdot {{\xi}_{y}} & -{{\xi}_x^{2}} & -{{\xi}_x}\cdot {{\xi}_{y}}\cr {{\xi}_x}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} & -{{\xi}_x}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}}\cr -{{\xi}_x^{2}} & -{{\xi}_x}\cdot {{\xi}_{y}} & {{\xi}_x^{2}} & {{\xi}_x}\cdot {{\xi}_{y}}\cr -{{\xi}_x}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}} & {{\xi}_x}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} \end{pmatrix}}
Je Stab setzen wir hier für die Parameter EA, ℓ, ξ die jeweiligen Größen ein.
/* Element-Stiffness Matrix from T123 */
k(EA,l,xi) := EA/l*matrix(
[ xi[1]^2,xi[1]*xi[2],-xi[1]^2,-xi[1]*xi[2]],
[ xi[1]*xi[2],xi[2]^2,-xi[1]*xi[2],-xi[2]^2],
[-xi[1]^2,-xi[1]*xi[2], xi[1]^2,xi[1]*xi[2]],
[-xi[1]*xi[2],-xi[2]^2,xi[1]*xi[2],xi[2]^2]);
Compose System-Matrix
Die Element-Steifigkeits-Matrizen ki addieren wir nun je Element zur System-Steifigkeitsmatrix K hinzu - so, wie im Prozess-Schema beschrieben:
Element 4 - die Feder mit der Steifigkeit k = κ* EA/ℓ addieren wir als letztes zu Element K44 hinzu.
In die Rechten Seite des Gleichungssystems schreiben wir nur die Kraft F in der zweiten Zeile.
Wir erhalten das Gesamt-Gleichungssystem zu
- Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \displaystyle \frac{EA}{\sqrt{2}\cdot a}\cdot \begin{pmatrix} \sqrt{2}+\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\sqrt{2} & 0\cr \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & 0 & 0\cr -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & 0 & 0\cr -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \kappa+\sqrt{2}+\frac{1}{2} & 0 & -\sqrt{2}\cr -\sqrt{2} & 0 & 0 & 0 & \sqrt{2} & 0\cr 0 & 0 & 0 & -\sqrt{2} & 0 & \sqrt{2} \end{pmatrix} \cdot\underline{Q}\,=\, \begin{pmatrix}0\cr -F\cr 0\cr 0\cr 0\cr 0\end{pmatrix}}
Wichtig für die Lösung des Gleichungssystems (bei hunderttausenden von Unbekannten) ist, dass die Systemmatrix die sympatische Eigenschaft hat, symmetrisch zu sein.
/* compose total stiffness matrix */
K: zeromatrix(2*dims[1],2*dims[1]);
for rod:1 thru dims[2] do
(/* Elemet Stiffness matrix for Element i*/
ESM : k(EA,l[rod],xi[rod]),
/* incidence Matrix*/
iL: [2*R[rod][1]-1,2*R[rod][1],2*R[rod][2]-1,2*R[rod][2]],
for rowi: 1 thru 4 do
for coli: 1 thru 4 do
(K[iL[rowi]][iL[coli]]:
K[iL[rowi]][iL[coli]]+ESM[rowi][coli]),
print("done adding ESM for rod ",rod))$
/*add spring*/
K[4,4] : K[4,4]+kappa*(EA/sqrt(2)/a);
/* right-hand-side in K*Q=P */
P: transpose(matrix([0,-F,0,0,0,0]));
/* print equations of "motion" */
fac: EA/(sqrt(2)*a);
print(fac,expand(K/fac),"∙",Q," = ", P)$
/* system mtrix is symmetric ? */
print("K ist symmtric?: ",is(K - transpose(K) = zeromatrix(2*dims[1],2*dims[1])))$
Incorporate Boudary Conditions
Randbedingungen für unsere Knoten-Koordinaten sind
- .
Wir arbeiten Sie in das lineare Gleichungssystem ein, indem wir die zugehörigen Zeilen und Spalten - 3, 5, 6 - streichen.
Nun lautet das Gleichungssystem
- Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \displaystyle \frac{EA}{\sqrt{2}\cdot a} \begin{pmatrix} \sqrt{2}+\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\cr \frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\cr -\frac{1}{2} & -\frac{1}{2} & \kappa+\sqrt{2}+\frac{1}{2}\end{pmatrix} \cdot \begin{pmatrix}{{u}_{I}}\cr {{v}_{I}}\cr {{v}_{II}} \end{pmatrix}\,=\, \begin{pmatrix}0\cr -F\cr 0 \end{pmatrix}}
/*incorporate boundary conditions */
K : submatrix(3,5,6,K,3,5,6);
Q : submatrix(3,5,6,Q);
P : submatrix(3,5,6,P);
print(fac,expand(K/fac),"∙",Q," = ", P)$
Solution
Die Lösung für κ=1/2 ist
- ,
oder numerisch
- Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \begin{array}{ll} {{u}_{1}}&=\frac{a\cdot F}{{EA}}\cr {{v}_{1}}&=-4.567223249782448\cdot \frac{a\cdot F}{{EA}}\\ {{u}_{2}}&=0.0\\ {{v}_{2}}&=-0.7387961250362585\cdot \frac{a\cdot F}{{EA}}\\ {{u}_{3}}&=0.0\\ {{v}_{3}}&=0.0\\ \end{array}} .
/* solve */
sol:makelist(Q[i][1]=ratsimp(linsolve_by_lu(K,P)[1][i][1]),i,1,3);
Post-Processing
Aus T312 wissen wir, dass je Stab
- .
Die Stab-Normalkraft ist
hier
- .
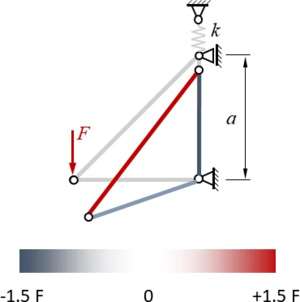
In FEM-Programmen werden Spannungen (hier die Normalkräfte) und Verformungen gern in ein Bild eingetragen, die Größe der Spannung wird dabei farblich kodiert:
declare("Δl", alphabetic);
sol: subst([kappa=1/2],append(sol, [u[2]=0,u[3]=0,v[3]=0]));
for rod:1 thru dims[2] do
(Δl[rod] : xi[rod].transpose(subst(sol,
[u[R[rod][2]]-u[R[rod][1]],v[R[rod][2]]-v[R[rod][1]]])),
S[rod] : EA/l[rod]*Δl[rod],
print("S[",rod,"] = ", expand(float(S[rod]))));
Wie passt diese Vorgehensweise nun zur klassischen Technischen Mechanik? Eigentlich gar nicht. Hier wird nichts freigeschnitten, es gibt keine Gleichgewichtsbedingungen je Element und keine Kraft-Übergangsbedingungen zwischen den Elementen. Wir brauchen also eine fundamental andere Mechanik, als die des gewohnten Kräftegleichgewichts.
Hier kommt die Analytische Mechanik, für die Methode der Finiten Elemente in Form des Prinzips der virtuellen Arbeit, ins Spiel. Sie erklärt, wie wir Übergangsbedingungen erfüllen, wie wir Spalten und Zeilen des Gleichungssystems erstellen und warum wir Randbedingungen einfach durch Streichen von Zeilen und Spalten der Systemmatrix erfüllen.
Grundlagen
Die Methode der Finiten Elemente (FEM) arbeitet mit dem Prinzip der virtuellen Verrückungen für die Gleichgewichtsbedingungen und einfachen, lokalen Polynom-Ansätzen.
Für die Gleichgewichtsbedingung brauchen wir die allgemeinen Terme der virtuellen Arbeit des Systems
wobei δΠ die Virtuelle Formänderungsenergie ist und δWa die virtuelle Arbeit von äußeren, eingeprägten Lasten.
Darin ist z.B. für den Euler-Bernoulli-Balken
Die gesamte Virtuelle Formänderungsarbeit setzt sich damm additiv aus den Anteilen aller N elastischen Bauteile zusammen, also
Die Arbeit von äußeren, eingeprägten Kräften ist beispielsweise
Das δΠ sieht ganz ähnlich aus wie die Formänderungsenergie Π der Potentiellen Energie - hier fehlt allerdings der Faktor 1/2!
Der Prozess, in dem wir eine Striktur in Finite Elemente unterteilen, nennen wir Diskretisierung. Denn an dieser Stellen werden aus den unendlich vielen Freiheitsgraden endlich viele.
Als Trial-Formfunktionen für die Approximation der exakten Lösung wählen wir Polynome, die wir in die Raumrichtungen aneinanderstückeln - und zwar immer wieder die selben! Jeder Abschnitt des Struktur,, in dem wir eine Trial-Funktion ansetzen, nennen wir Finites Element, jede "Stoßstelle" zwischen den Elementen nennen wir Node (Knoten). Was hier wenig dramatisch daherkommt, ist die Grundlage für den unglaublichen Erfolg der FEM:
- Wiederholung: Alle Trial-Funktionen sind gleich!
- Simplizität: Jede Trial-Funktion ist ein sehr einfaches Polynom - oft reicht erster Ordnung!
- Skalierbarkeit: die Genauigkeit steigern wir durch die Unterteilung in kleinere Finite Elemente!
Stab-Modelle
Für einen geraden Stab sieht eine Diskretisierung - hier mit gleich langen - Finiten Elementen so aus:
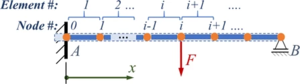
Der Ansatz - hier für einen Euler-Bernoulli-Balken - ist wieder allgemein
wobei die ϕi die linear unabhängigen Trial-Funktionen und die Qi ihre gesuchten "Wichtungsfaktoren" - hier: die gesuchten Auslenkungen und/oder Verdrehungen an den Knoten - sind.
Statt Polynome zu wählen, die sich über die gesamte Stab-Länge erstrecken wie beim Verfahren von Ritz, wählen wir hier lokale Ansatzfunktionen je Element, also
Schalen-Modelle
Bei Schalen-Modellen für ebene Strukturen müssen wir Verschiebungen und/oder Verdrehungen als Funktion von zwei unabhängigen Variablen - z.B. x und y - ausdrücken.
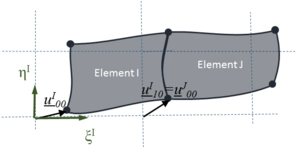
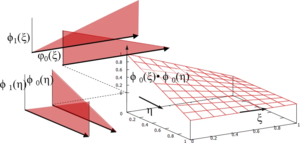
Als Ansatz für eine ebene Scheibe sind die Verschiebungen in der der Schalen-Ebene in die beiden Raumrichtungen
In den Knoten-Verschiebungen uij stehen dann die beiden Knoten-Verschiebungen Qij, Qkl, also
die wir wiederum in die Spaltenmatrix der gesuchten Größen Q einsortieren:
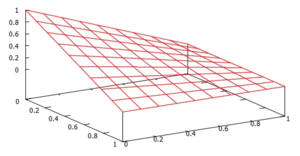
Mit linearen Trial-Functions wird die Näherungslösung je Element dann aus diesen Formen zusammengesetzt sein:
 |
 |
Das Gleichungssystem für lineare Bewegungsgleichungen
Weil die Ansatzfunktionen nur im Element gelten, ist
die Summe aller virtuellen Formänderungs-Energien aller Elemente.
Einsetzen und Ausführen der Integration in δΠ führt bei linearen Systemen (wir betrachten nur lineare Systeme) immer auf die Form
und δWa hat in der Statik immer die Form
also
Die Gleichgewichtsbedingungen des Prinzip der virtuellen Verrückungen lauten:
und das sind mehrere, denn:
- die einzelnen virtuellen Verrückungen in δW sind jeweils für sich unabhängig. Die Summe der
wird nur dann Null, wenn die Klammerausdrücke jeweils für sich verschwinden (Null werden). - Wir erhalten also ganz automatisch für jede unbekannte Koordinate eine Gleichgewichtsbedingung.
Ansatzfunktionen
Finite Elemente benutzen besondere Trial-Functions um die Verschiebungen einer Struktur sehr effizient abbilden zu können. Dies sind
Im Vergleich: das Verfahren von Ritz und die Methode der Finite Elemente
Literatur
- Strang 2008
Untergeordnete Seiten
Links