Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode

Die Methode der Finiten Elemente ist deshalb so erfolgreich, weil Sie ideal mit der Implementierung im Computer harmoniert.

Auf zwei Ansätzen basiert dieser Erfolg:

	Die komplette Struktur wird in kleine Elemente - die Finiten Elemente - aufgeteilt. Ihre Bewegung wird durch diskrete Knoten-Koordinaten erfasst, die wie  bei einem Puzzle zusammenpassen. Alles, was im Element-Inneren "passiert", wird durch die Knoten-Koordinaten erfasst. Die Beschreibung der Struktur wird also komplett auf diese Koordinaten-Koordinaten reduziert.
	Der Beitag jedes elastischen Elements wird additiv zum Gesamtsystem hinzugefügt. Diese Einzel-Beträge heißen Element-Steifigkeitsmatrix. Schnittbilder und Schnittlasten brauchen wir nicht dafür!

Einführungsbeispiel

Wie das geht, zeige ich Ihnen - zuerst ohne Theorie - für ein Beispiel:

Stabwerk

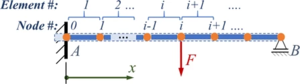
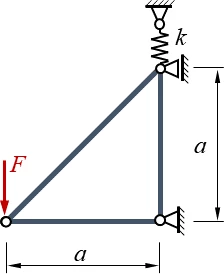
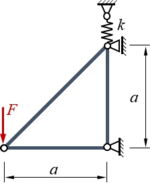Ein Stabwerk aus drei elastischen Stäben und einer Feder wird durch eine Einzelkraft F belastet. Alle Stäbe haben die Dehnsteifigkeit EA, die Federsteifigkeit ist k.

Gegeben sind a, EA, k, F, gesucht sind die Verschiebungen der Knotenpunkte.

Die Lösung mit der Methode der Finiten Elemente zeige ich Ihnen aus drei Perspektiven:

1. das Prozess-Schema
2. die Lehrbuch-Sichweise und
3. die Implementierung in einem Algorithmus (hier Maxima).

Das Modell für ein lineares Modell mit Finiten Elemente ist ein System linearer Gleichungen. In jeder Spalte steht die Gleichgewichtsbedingung für eine Koordinate Q_i, in den Spalten stehen die Koeffizienten der Koordinaten Q_j. Das Gleichungssystem sieht immer so aus:

${\underline {\underline {K}}}\cdot {\underline {Q}}={\underline {P}}$

Wir benennen Stäbe und Knoten, ein Koordinatensystem brauchen wir auch:

Benennung von Stäben und Knoten.

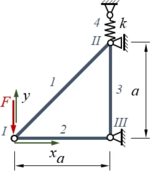
Das Stabwerk besteht aus vier elastischen Bauteilen:

• den Stäben 1,2 und 3 sowie
• der Feder.

Und jedes dieser elastischen Bauteil hinterlässt eine Spur in der Steifigkeitsmatrix K.

Die Verformung der Stäbe erfassen wir durch die Verschiebung der Endpunkte - der Knoten - des Stabwerks. Wie das geht und wir wir daraus eine Element-Steifigkeitsmatrix für einen Dehnstab bekommen, steht in T312. Die Knoten-Verschiebungen schreiben wir in Q hinein, hier für drei Knoten die Verschiebungen jeweils u in x- und v in y-Richtung

A. Das Prozess-Schema

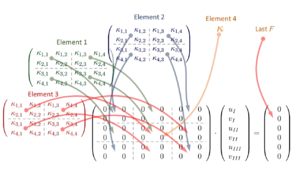
Das Gesamt-Gleichungssystem komponieren wir, indem die Element-Steifigkeitsmatrizen je Bauteil nach einem festen Schema in K hineinkopiert werden:

Prozessschema FEM

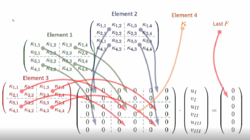
Es bleibt noch, die Randbedingungen in das System einzuarbeiten: das machen wir durch Streichen der Zeilen und Spalten des Gleichungssystems, die zu Koordinaten gehören, die aufgrund der Lagerung des Systems behindert sind:

Randbedingungen einarbeiten.

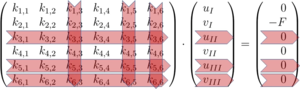
Wie dieser Prozess in einem "Lehrbuch" der Mechanik / Mathematik und in einer Implementierung im Computer aussieht folgt hier in der linken bzw. rechten Spalte:

B: Die Lehrbuch-Sichtweise

C: Die Implementierung in MAXIMA

Header

Für diese Aufgabe nutzen wir Ergenisse aus T312.

In diesem Beispiel sind die gesuchten Größen die Verschiebungen der drei Knoten in x- und y-Richtung, also:

${\underline {Q}}=\left({\begin{array}{l}u_{I}\\v_{I}\\u_{II}\\v_{II}\\u_{III}\\v_{III}\\\end{array}}\right)$

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2018-05-30                            */
/* ref: FEM                                            */
/* description: Berechnung der Knoten-Verscheibungen   */
/*              eines elastischen Stabwerks            */
/*              - gehört zu Aufgabe T312               */
/*******************************************************/
 
/* coordiates in K*Q=P */
Q: transpose(matrix(flatten(makelist([u[i],v[i]],i,1,length(N)))));

System Parameter

Die Knoten (Nodes) I, II und III des Fachwerks haben die Koordinaten [x_i, y_i]:

${\begin{array}{llcc}N_{1}=&[&0,&0]\\N_{2}=&[&a,&a]\\N_{3}=&[&a,&0]\end{array}}$

Jeder Stab (Rod) ist ein Finites Element des Fachwerks, die drei Stabe verbinden folgende Knoten miteinander:

${\begin{array}{llcc}R_{1}=&[&1,&2]\\R_{2}=&[&1,&3]\\R_{3}=&[&2,&3]\end{array}}$

Damit berechnen wir die Parameter [ξ_x, ξ_x] aus T312

${\begin{array}{ll}\ldots {\text{ für Element 1:}}&\displaystyle [\xi _{x},\xi _{y}]=[{\frac {1}{\sqrt {2}}},{\frac {1}{\sqrt {2}}}]\\\ldots {\text{ für Element 2:}}&\displaystyle [\xi _{x},\xi _{y}]=[1,0]\\\ldots {\text{ für Element 3:}}&\displaystyle [\xi _{x},\xi _{y}]=[0,-1]\end{array}}$,

die wir für den nächsten Schritt brauchen:

/* parameters */
assume(a>0);
 
/* nodal coordinates */
N : [[0, 0],
     [a, a],
     [a, 0]];
/* rod-connectivity */
R : [[1,2],
     [1,3],
     [2,3]];
dims: [length(N),length(R)];


/* compute elements of Element-Stiffness Matrix */
/* Δx / Δy */
d : makelist(N[R[i][2]]-N[R[i][1]],i,1,length(R));
/* reference-lengths */
l : makelist(sqrt(d[i].d[i]),i,1,length(d));
/* normalized Δx / Δy ( xi )*/
xi : makelist((N[R[i][2]]-N[R[i][1]])/l[i],
                                     i,1,length(R));

Definition of the Element Stiffness-Matrix

Die Element-Steifigkeitsmatrix aus T312 sieht so aus:

Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle k\left(EA,\ell,\xi\right) := \displaystyle \frac{EA}{\ell} \cdot \begin{pmatrix} {{\xi}_x^{2}} & {{\xi}_x}\cdot {{\xi}_{y}} & -{{\xi}_x^{2}} & -{{\xi}_x}\cdot {{\xi}_{y}}\cr {{\xi}_x}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} & -{{\xi}_x}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}}\cr -{{\xi}_x^{2}} & -{{\xi}_x}\cdot {{\xi}_{y}} & {{\xi}_x^{2}} & {{\xi}_x}\cdot {{\xi}_{y}}\cr -{{\xi}_x}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}} & {{\xi}_x}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} \end{pmatrix}}

Je Stab setzen wir hier für die Parameter EA, ℓ, ξ die jeweiligen Größen ein.

Compose System-Matrix

Die Element-Steifigkeits-Matrizen k_i addieren wir nun je Element zur System-Steifigkeitsmatrix K hinzu - so, wie im Prozess-Schema beschrieben:

Element 4 - die Feder mit der Steifigkeit k = κ* EA/ℓ addieren wir als letztes zu Element K₄₄ hinzu.

In die Rechten Seite des Gleichungssystems schreiben wir nur die Kraft F in der zweiten Zeile.

Wir erhalten das Gesamt-Gleichungssystem zu

Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \displaystyle \frac{EA}{\sqrt{2}\cdot a}\cdot \begin{pmatrix} \sqrt{2}+\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\sqrt{2} & 0\cr \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & 0 & 0\cr -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & 0 & 0\cr -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \kappa+\sqrt{2}+\frac{1}{2} & 0 & -\sqrt{2}\cr -\sqrt{2} & 0 & 0 & 0 & \sqrt{2} & 0\cr 0 & 0 & 0 & -\sqrt{2} & 0 & \sqrt{2} \end{pmatrix} \cdot\underline{Q}\,=\, \begin{pmatrix}0\cr -F\cr 0\cr 0\cr 0\cr 0\end{pmatrix}}

Wichtig für die Lösung des Gleichungssystems (bei hunderttausenden von Unbekannten) ist, dass die Systemmatrix die sympatische Eigenschaft hat, symmetrisch zu sein.

Incorporate Boudary Conditions

Randbedingungen für unsere Knoten-Koordinaten sind

${\begin{array}{ll}u_{II}&=0\\v_{III}&=0\\u_{III}&=0\end{array}}$.

Wir arbeiten Sie in das lineare Gleichungssystem ein, indem wir die zugehörigen Zeilen und Spalten - 3, 5, 6 - streichen.

Nun lautet das Gleichungssystem

Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \displaystyle \frac{EA}{\sqrt{2}\cdot a} \begin{pmatrix} \sqrt{2}+\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\cr \frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\cr -\frac{1}{2} & -\frac{1}{2} & \kappa+\sqrt{2}+\frac{1}{2}\end{pmatrix} \cdot \begin{pmatrix}{{u}_{I}}\cr {{v}_{I}}\cr {{v}_{II}} \end{pmatrix}\,=\, \begin{pmatrix}0\cr -F\cr 0 \end{pmatrix}}

Solution

Die Lösung für κ=1/2 ist

${\begin{array}{ll}{{u}_{I}}&\displaystyle ={\frac {a\cdot F}{EA}}\\{{v}_{I}}&\displaystyle =-{\frac {\left(22639305+4002171\cdot {{2}^{\frac {5}{2}}}\right)\cdot a\cdot F}{\left(438075\cdot {{2}^{\frac {7}{2}}}+4957649\right)\cdot EA}}\\{{v}_{II}}&\displaystyle =-{\frac {\left(17144+5993\cdot {{2}^{\frac {3}{2}}}\right)\cdot a\cdot F}{\left(1017\cdot {{2}^{\frac {9}{2}}}+23137\right)\cdot EA}}\end{array}}$,

oder numerisch

Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \begin{array}{ll} {{u}_{1}}&=\frac{a\cdot F}{{EA}}\cr {{v}_{1}}&=-4.567223249782448\cdot \frac{a\cdot F}{{EA}}\\ {{u}_{2}}&=0.0\\ {{v}_{2}}&=-0.7387961250362585\cdot \frac{a\cdot F}{{EA}}\\ {{u}_{3}}&=0.0\\ {{v}_{3}}&=0.0\\ \end{array}} .

Post-Processing

Aus T312 wissen wir, dass je Stab

$\Delta \ell _{i}=\xi _{x}\cdot \Delta u_{i}+\xi _{y}\cdot \Delta v_{i}$.

Die Stab-Normalkraft ist

$S_{i}=\displaystyle {\frac {EA}{\ell _{i}}}\cdot \Delta \ell _{i}$

hier

${\begin{array}{ll}S_{1}\,=\,&1.414213562373095\cdot F\\S_{2}\,=\,-&0.7387961250362585\cdot F\\S_{3}\,=\,-&1.0\cdot F\end{array}}$.

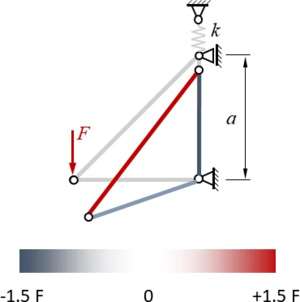
In FEM-Programmen werden Spannungen (hier die Normalkräfte) und Verformungen gern in ein Bild eingetragen, die Größe der Spannung wird dabei farblich kodiert:

Wie passt diese Vorgehensweise nun zur klassischen Technischen Mechanik? Eigentlich gar nicht. Hier wird nichts freigeschnitten, es gibt keine Gleichgewichtsbedingungen je Element und keine Kraft-Übergangsbedingungen zwischen den Elementen. Wir brauchen also eine fundamental andere Mechanik, als die des gewohnten Kräftegleichgewichts.

Hier kommt die Analytische Mechanik, für die Methode der Finiten Elemente in Form des Prinzips der virtuellen Arbeit, ins Spiel. Sie erklärt, wie wir Übergangsbedingungen erfüllen, wie wir Spalten und Zeilen des Gleichungssystems erstellen und warum wir Randbedingungen einfach durch Streichen von Zeilen und Spalten der Systemmatrix erfüllen.

---

Produktansatz der Trialfunctions.

Produktansatz mit linearen Trialfunctions.

Knoten und Elemente für Stabmodelle.

Plattenmodell

Stabwerk

Komposition der Steifigkeitsmatrix.

Verformung des Stabwerks.

Untergeornete Seiten

1. FEM: Trial-Functions für kubische Ansatz-Polynome
2. FEM: Trial-Functions für lineare Ansatz-Polynome