Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 8: | Zeile 8: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
|[[Datei:FIniteElementeMethode-Puzzel.png|Passt!]] | |[[Datei:FIniteElementeMethode-Puzzel.png|50px|Passt!]] | ||
|Die komplette Struktur wird in kleine Elemente - die Finiten Elemente - aufgeteilt. Ihre Bewegung wird durch diskrete Knoten-Koordinaten erfasst, die wie bei einem Puzzle zusammenpassen. Alles, was im Element-Inneren "passiert", wird durch die Knoten-Koordinaten erfasst. | |Die komplette Struktur wird in kleine Elemente - die Finiten Elemente - aufgeteilt. Ihre Bewegung wird durch diskrete Knoten-Koordinaten erfasst, die wie bei einem Puzzle zusammenpassen. Alles, was im Element-Inneren "passiert", wird durch die Knoten-Koordinaten erfasst. | ||
Die Beschreibung der Struktur wird also komplett auf diese Koordinaten-Koordinaten reduziert. | Die Beschreibung der Struktur wird also komplett auf diese Koordinaten-Koordinaten reduziert. | ||
|- | |- | ||
|[[Datei:FiniteElementeMethode-Plus.png|Plus!]] | |[[Datei:FiniteElementeMethode-Plus.png|50px|Plus!]] | ||
|Der Beitag jedes elastischen Elements wird additiv zum Gesamtsystem hinzugefügt. Diese Einzel-Beträge heißen Element-Steifigkeitsmatrix. | |Der Beitag jedes elastischen Elements wird additiv zum Gesamtsystem hinzugefügt. Diese Einzel-Beträge heißen Element-Steifigkeitsmatrix. | ||
Schnittbilder und Schnittlasten brauchen wir nicht dafür! | Schnittbilder und Schnittlasten brauchen wir nicht dafür! | ||
| Zeile 19: | Zeile 19: | ||
=Einführungsbeispiel= | =Einführungsbeispiel= | ||
Wie das geht, zeige ich Ihnen - zuerst ohne Theorie - für ein Beispiel: | Wie das geht, zeige ich Ihnen - zuerst ohne Theorie - für ein Beispiel: | ||
<table> | <table> | ||
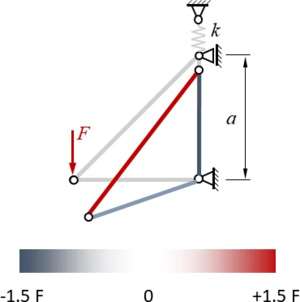
<tr><td>[[Datei:FiniteElementeMethode-Stabwerk.png|mini|Stabwerk]] | <tr><td>[[Datei:FiniteElementeMethode-Stabwerk.png|mini|Stabwerk]] | ||
</td><td>Ein Stabwerk aus drei elastischen Stäben und einer Feder wird durch eine Einzelkraft ''F'' belastet. Alle Stäbe haben die Dehnsteifigkeit ''EA'', die Federsteifigkeit ist ''k''.</td></tr> | </td><td>Ein Stabwerk aus drei elastischen Stäben und einer Feder wird durch eine Einzelkraft ''F'' belastet. Alle Stäbe haben die Dehnsteifigkeit ''EA'', die Federsteifigkeit ist ''k''.</td></tr> | ||
</table> | </table> | ||
Gegeben sind ''a, EA, k, F'', gesucht sind die Verschiebungen der Knotenpunkte. | |||
Die Lösung mit der Methode der Finiten Elemente zeige ich Ihnen aus drei Perspektiven: | |||
<ol type="A"> | |||
<li>das Prozess-Schema</li> | |||
<li>die Lehrbuch-Sichweise und</li> | |||
<li>die Implementierung in einem Algorithmus (hier Maxima).</li> | |||
</ol> | |||
Das Modell für ein lineares Modell mit Finiten Elemente ist ein System linearer Gleichungen. In jeder Spalte steht die Gleichgewichtsbedingung für eine Koordinate ''Q<sub>i</sub>'', in den Spalten stehen die Koeffizienten der Koordinaten ''Q<sub>j</sub>''. Das Gleichungssystem sieht immer so aus: | |||
Wir benennen Stäbe und Knoten, ein Koordinatensystem brauchen wir auch: | |||
Das Stabwerk besteht aus vier elastischen Bauteilen: | |||
* den Stäben 1,2 und 3 sowie | |||
* der Feder. | |||
Und jedes dieser elastischen Bauteil hinterlässt eine Spur in der Steifigkeitsmatrix ''K''. | |||
Die Verformung der Stäbe erfassen wir durch die Verschiebung der Endpunkte - der Knoten - des Stabwerks. Wie das geht und wir wir daraus eine Element-Steifigkeitsmatrix für einen Dehnstab bekommen, steht in T312. Die Knoten-Verschiebungen schreiben wir in ''Q'' hinein, hier für drei Knoten die Verschiebungen jeweils ''u'' in ''x-'' und ''v'' in ''y-''Richtung | |||
== A. Das Prozess-Schema == | |||
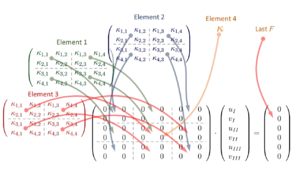
Das Gesamt-Gleichungssystem komponieren wir, indem die Element-Steifigkeitsmatrizen je Bauteil nach einem festen Schema in ''K'' hineinkopiert werden: | |||
Version vom 20. Februar 2021, 19:22 Uhr
Die Methode der Finiten Elemente ist deshalb so erfolgreich, weil Sie ideal mit der Implementierung im Computer harmoniert.
Auf zwei Ansätzen basiert dieser Erfolg:
Einführungsbeispiel
Wie das geht, zeige ich Ihnen - zuerst ohne Theorie - für ein Beispiel:
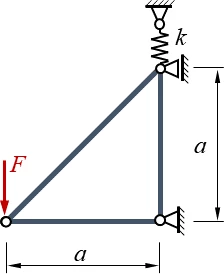 | Ein Stabwerk aus drei elastischen Stäben und einer Feder wird durch eine Einzelkraft F belastet. Alle Stäbe haben die Dehnsteifigkeit EA, die Federsteifigkeit ist k. |
Gegeben sind a, EA, k, F, gesucht sind die Verschiebungen der Knotenpunkte.
Die Lösung mit der Methode der Finiten Elemente zeige ich Ihnen aus drei Perspektiven:
- das Prozess-Schema
- die Lehrbuch-Sichweise und
- die Implementierung in einem Algorithmus (hier Maxima).
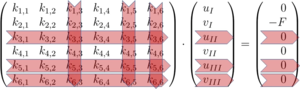
Das Modell für ein lineares Modell mit Finiten Elemente ist ein System linearer Gleichungen. In jeder Spalte steht die Gleichgewichtsbedingung für eine Koordinate Qi, in den Spalten stehen die Koeffizienten der Koordinaten Qj. Das Gleichungssystem sieht immer so aus:
Wir benennen Stäbe und Knoten, ein Koordinatensystem brauchen wir auch:
Das Stabwerk besteht aus vier elastischen Bauteilen:
- den Stäben 1,2 und 3 sowie
- der Feder.
Und jedes dieser elastischen Bauteil hinterlässt eine Spur in der Steifigkeitsmatrix K.
Die Verformung der Stäbe erfassen wir durch die Verschiebung der Endpunkte - der Knoten - des Stabwerks. Wie das geht und wir wir daraus eine Element-Steifigkeitsmatrix für einen Dehnstab bekommen, steht in T312. Die Knoten-Verschiebungen schreiben wir in Q hinein, hier für drei Knoten die Verschiebungen jeweils u in x- und v in y-Richtung
A. Das Prozess-Schema
Das Gesamt-Gleichungssystem komponieren wir, indem die Element-Steifigkeitsmatrizen je Bauteil nach einem festen Schema in K hineinkopiert werden:

Untergeornete Seiten
