Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Differenzen Verfahren (EBB)

Das Differenzenverfahren ersetzt die Bewegungsgleichung des Euler-Bernoulli-Balkens im Gebiet (die Differentialgleichung) durch den Differenzenquotienten.

Also wird aus

${\frac {d\,w}{d\,x}}|_{x=x_{i}}={\frac {\mathrm {w} \left(x_{i}+{\mathit {\Delta x}}\right)-\mathrm {w} \left(x_{i}\right)}{\mathit {\Delta x}}}$

mit endlich großem Δx. Wir wählen

$x_{i+1}=x_{i}+\Delta \,x$,

so dass wir die erste Ableitung der Funktion w(x) an N Stellen x_i bequem durch N+1 viele Stützstellen W_i := w(x_i) berechnen können.

Feld-Differentialgleichung

Wie klappt das für die vierte Ableitung in

$EI\cdot w^{IV}=q$?

Maxima

Indem wir die vierte Ableitung eines Polynoms, das durch benachbarte Punkte der Stützstellen verläuft, bestimmen und dies als vierten Ableitung der gesuchten Funktion verwenden. Wir erfassen Ableitungen der gesuchten Verschiebung durch Linearkombinationen der Stützstellen. Dazu brauchen wir mindestens ein Polynom 4ter Ordnung, damit wir es vier mal ableiten können, ohne dass es dabei verschwindet (Null wird). Wir wählen also 5 äquidistante Stützstellen um xi herum und sampeln die x-Koordinate ξ, die unbekannte Auslenkung Wj und den Wert der bekannten Streckenlast qj: ${\begin{array}{crllll}[&-2\cdot \Delta x+&{{x}_{i}}&,{{W}_{i-2}}&,q_{i-2}&],\\[][&-\Delta x+&{{x}_{i}}&,{{W}_{i-1}}&,q_{i-1}&],\\[][&&{{x}_{i}}&,{{W}_{i}}&,q_{i}&],\\[][&&{{x}_{i}}+\Delta x&,{{W}_{i+1}}&,q_{i+1}&],\\[][&&{{x}_{i}}+2\cdot \Delta x&,{{W}_{i+2}}&,q_{i+2}&]\end{array}}$ Das Polynom 4ter Ordnung dazu ist $p={{C}_{4}}\cdot {{x}^{4}}+{{C}_{3}}\cdot {{x}^{3}}+{{C}_{2}}\cdot {{x}^{2}}+{{C}_{1}}\cdot x+{{C}_{0}}$ und dessen vierte Ableitung ${\begin{array}{rl}\kappa =&\displaystyle {\frac {d^{4}\,p}{d\,x^{4}}}\\=&4\cdot 3\cdot 2\cdot 1\cdot C_{4}\\=&\displaystyle {\frac {{{W}_{i-2}}-4\cdot {{W}_{i-1}}+6\cdot {{W}_{i}}-4\cdot {{W}_{i+1}}+{{W}_{i+2}}}{{\Delta x}^{4}}}\end{array}}$, wobei wir die Ci aus der Anpassung an die Stützstellen erhalten. Wie das im Detail geht, steht in Kit6.

/* Maxima Sourcecode */ declare("Δx", alphabetic); dgl: 'diff(w,x,4)=q/EI; /*samples */ S : makelist([x[0]+j*Δx,W[i+j]],j,-2,2); /* polynom */ p : sum(C[j]*x^j,j,0,4); /* equations */ equs : makelist(subst([x=S[j][1]],p)=S[j][2],j,1,5); /* unknown coefficients */ coef : makelist(C[j],j,0,4); /* solution */ sol : linsolve(equs,coef); /* 4th derivative*/ kappa : diff(p,x,4); kappa : subst(sol,kappa); print(dgl," -> ", subst(['diff(w,x,4)=kappa],dgl)); ole : Δx^4*subst(['diff(w,x,4)=kappa],dgl);

Die vierte Ableitung κ des Polynoms p setzen wir nun anstelle der Ableitung in unserer Differentialbeziehung an, aus unserer Biege-Differentialgleichung wird die Biege-Differenzenbeziehung

$\displaystyle {\frac {{{W}_{i-2}}-4\cdot {{W}_{i-1}}+6\cdot {{W}_{i}}-4\cdot {{W}_{i+1}}+{{W}_{i+2}}}{{\Delta x}^{4}}}={\frac {q_{i}}{E\;I}}$

Für jede Stützstelle W_i im Gebiet muss nun diese gewöhnliche, lineare Gleichung erfüllt sein, so dass ein Gleichungssystem für die W_i zunächst so aussieht:

$\left({\begin{array}{rrrrrrr}\\\ddots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\\\...&+1&-4&+6&-4&+1&...\\\\\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\ddots \\\\\end{array}}\right)\cdot \left({\begin{array}{l}\vdots \\W_{i-2}\\W_{i-1}\\W_{i}\\W_{i+1}\\W_{i+2}\\\vdots \\\end{array}}\right)=\left({\begin{array}{c}\vdots \\\vdots \\\vdots \\\displaystyle {\frac {q_{i}}{EI}}\cdot \Delta x^{4}\\\vdots \\\vdots \\\vdots \\\end{array}}\right)$,

allgemein mit der Systemmatrix A, den Unbekannten W und der rechten Seite b

${\underline {\underline {A}}}\cdot {\underline {W}}={\underline {b}}$.

Sie sehen sofort: das geht an den Rändern schief:

• an der Stelle x=0 gibt es "links" neben W₀ keine Stützstellen W_0-1, W_0-2 mehr - genauso fehlen am "rechten" zwei Stützstellen.

Und

• uns fehlen noch die Randbedingungen in der Formulierung des Problems!

Wir lösen beide Probleme pragmatisch: wir erweitern die Anzahl der Gleichungen in A und gesuchten Größen W an jedem Rand um zwei - also um vier. Diese vier zusätzlichen Gleichungen nutzen wir nun zur Einarbeitung unserer Randbedingungen.

Wir schreiben nun alle Rand- und Übergangs-Bedingungen für die Biegelinie w(x) auf die Stützstellen W_j und q_j um:

Rand- und Übergangs-Bedingungen für behinderte Freiheitsgrade

Für Lager, die einzelne Freiheitsgrade behindern (hier w oder w') ersetzen wir einzelne Zeilen der Systemmatrix A durch die geometrische Zwangsbedingung:

Z.B. für

• w(ξ) = 0: An dieser Stützstelle ist der Wert  ::$W_{i}=0$, die Zeile des Gleichungssystems lautet:  ::$\left({\begin{array}{rrrrr}\ddots &\vdots &\vdots &\vdots &\vdots \\...&0&1&0&...\\\vdots &\vdots &\vdots &\vdots &\ddots \\\end{array}}\right)\cdot \left({\begin{array}{l}\vdots \\W_{i}\\\vdots \end{array}}\right)=\left({\begin{array}{c}\vdots \\0\\\vdots \end{array}}\right)$.
• w'(ξ) = 0: An dieser Stelle stellen wir die horizontale Tangente der Biegelinie durch  ::$\displaystyle {\frac {W_{i+1}-W_{i-1}}{2\cdot \Delta x}}=0$, die Zeile des Gleichungssystems lautet:

  $\left({\begin{array}{rrrrr}\ddots &\vdots &\vdots &\vdots &\vdots \\\\...&-1&0&1&...\\\\\vdots &\vdots &\vdots &\vdots &\ddots \\\end{array}}\right)\cdot \left({\begin{array}{l}\vdots \\W_{i-1}\\W_{i}\\W_{i+1}\\\vdots \end{array}}\right)=\left({\begin{array}{c}\vdots \\0\\\vdots \end{array}}\right)$.

  Äußere Kräfte- und Momente

  ... im Feld

  Um äußere, diskrete Lasten auf unser Finite-Differenzen-Modell im Feld einzubeziehen, interpretieren wir

  ${\displaystyle }$,

  als diskrete Kraft auf unser System an den Stützstellen. Denen können wir auch äußere Lasten hinzufügen, nämlich

  • die eingeprägte, äußere Kraft F_i und
  • das eingeprägte, äußere Moment M_i durch das Kräftepaar

  ${\begin{array}{ll}w(x_{i})&=W_{i}\\w'(x_{i})&=\displaystyle {\frac {-W_{i-1}+W_{i+1}}{2\cdot \Delta x}}\\w''(x_{i})&=\displaystyle {\frac {+W_{i-1}-2\,W_{i}+W_{i+1}}{\Delta x^{2}}}\\w'''(x_{i})&=\displaystyle {\frac {-W_{i-2}+2\,W_{i-1}-2\,W_{i+1}+W_{i+2}}{2\cdot \Delta x^{3}}}\\w''''(x_{i})&=\displaystyle {\frac {+W_{i-2}-4\,W_{i-1}+6\,W_{i}-4\,W_{i+1}+W_{i+2}}{\Delta x^{4}}}\\\end{array}}$.

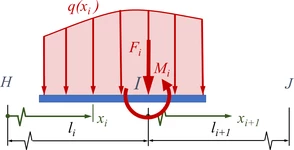
  Streckenlast und äußere Lasten im kontinuierlichen Fall um den Knoten I herum.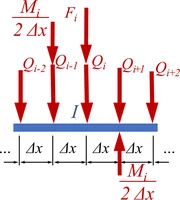

  Streckenlast und äußere Lasten im Fall von endlichen Differenzen um den Knoten I herum.

  Dazu müssen die Stützstellen mit den Last-Einleitungsstellen zusammenfallen!

  ... am Rand

  • Wir müssen unserer Stützstellen-Liste
    • eine Anfangs- bzw. End-Krümmung (2te Ableitung) für ein dort angreifendes Moment M = -EI w'' oder / und
    • eine vordefinierte 3te Ableitung für eine dort angreifende Querkraft Q = -EI w''' mitgeben.
    Die erforderlichen weiteren Beziehungen zwischen den Ableitungen von w und deren Erfassung durch die Stützstellen W_i sind

    ${\begin{array}{ll}w(x_{i})&=W_{i}\\w'(x_{i})&=\displaystyle {\frac {-W_{i-1}+W_{i+1}}{2\cdot \Delta x}}\\w''(x_{i})&=\displaystyle {\frac {+W_{i-1}-2\,W_{i}+W_{i+1}}{\Delta x^{2}}}\\w'''(x_{i})&=\displaystyle {\frac {-W_{i-2}+2\,W_{i-1}-2\,W_{i+1}+W_{i+2}}{2\cdot \Delta x^{3}}}\\w''''(x_{i})&=\displaystyle {\frac {+W_{i-2}-4\,W_{i-1}+6\,W_{i}-4\,W_{i+1}+W_{i+2}}{\Delta x^{4}}}\\\end{array}}$

     (vgl. Kit6). Da wir für jeden Rand des Euler-Bernoulli-Balkens genau zwei Randbedingungen erhalten, verbrauchen wir dafür genau 4 Gleichungen. Wir ersetzen also vier Gleichungen der Biegedifferentialgleichung durch vier Gleichungen der Randbedingungen.

    Macht das Verfahren Sinn?

    Das Finite-Differenzen-Verfahren erscheint also auf den ersten Blick anschaulich und intuitiv, ist aber numerisch ineffizient und basiert auf fragwürdigen mathematischen Ansätzen.

    • Es setzt als Näherungslösung für die Differentialbeziehung einer kontinuierlichen Funktion w im Feld des Euler-Bernoulli-Balkens ein gewöhnliches Gleichungssystem mit einigen 100 Stützstellen (= Unbekannten) an. Für die analytische Lösung brauchen wir gerade mal 4 Unbekannte (= Integrationskonstanten) je Feld!
    • Für Randwertprobleme mit linearen, partiellen Differentialgleichungen - z.B. für Schalen, bei denen man üblicherweise keine analytische Lösung findet - kann man das Verfahren sinnvoller einsetzen. Heute gibt es jedoch mit der Methode der Finiten Elemente deutlich effizientere Lösungsverfahren.
    • Der zentrale Ansatz des Verfahrens - das Ersetzen der Differentialbeziehung durch eine Differenzenbeziehung - nutzt kein mathematisch begründetes Näherungsverfahren.