Sources/Lexikon/Unabhängige Koordinaten: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „lköälökl“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Eine Position ''P'' auf der Erde wird durch die geographische Breite (latitude) ''φ'' und die geographische Länge (longitude) ''λ'' bestimmt (nach DIN 13312). | |||
[[Datei:Latitude and longitude graticule on a sphere.png|left|mini|By Peter Mercator [Public domain], via Wikimedia Commons]]<br clear="all"/> | |||
Zusammen mit der Höhe ''h'' über NN gibt das Tripel (φ, λ, h) eindeutig eine Position - die Koordinaten - auf der Erdoberfläche an. ''P'' kann also der "Name" für einen Materiepunkt sein, der z.B. einen Stein in Reykjavik. | |||
Die Koordinaten gelten bzgl. des Referenzsystems, hier dem Geozentrischen Referenzsystem (ECEF, earth-centered, earth fixed) . | |||
(''φ, λ, h'') hängen nicht von der Zeit oder einem anderen Parameter ab - sie sind unabhängig, die Koordinaten heißen unabhängige Koordinaten. Bezüglich diesen Referenzsystems hat 'P' keine Gescheindigkeit. | |||
Den Ortsvektor | |||
::<math>\vec{r}_P</math> | |||
zu ''P'' kann man mit verschiedenen unabhängigen Koordinaten beschreiben - wir könnten auch (''x, y, z'') nehmen - entscheidend für unsere Wahl ist nur, was wir besser denken können. | |||
[[Datei:Tm-C-1.1.2.-03.png|links|mini|Based on an Image by Freepik]]<br clear="all"/> | |||
Version vom 20. Februar 2021, 15:29 Uhr
Eine Position P auf der Erde wird durch die geographische Breite (latitude) φ und die geographische Länge (longitude) λ bestimmt (nach DIN 13312).
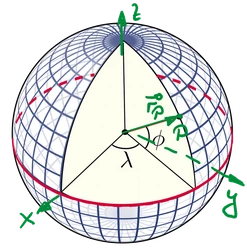
Zusammen mit der Höhe h über NN gibt das Tripel (φ, λ, h) eindeutig eine Position - die Koordinaten - auf der Erdoberfläche an. P kann also der "Name" für einen Materiepunkt sein, der z.B. einen Stein in Reykjavik.
Die Koordinaten gelten bzgl. des Referenzsystems, hier dem Geozentrischen Referenzsystem (ECEF, earth-centered, earth fixed) .
(φ, λ, h) hängen nicht von der Zeit oder einem anderen Parameter ab - sie sind unabhängig, die Koordinaten heißen unabhängige Koordinaten. Bezüglich diesen Referenzsystems hat 'P' keine Gescheindigkeit.
Den Ortsvektor
zu P kann man mit verschiedenen unabhängigen Koordinaten beschreiben - wir könnten auch (x, y, z) nehmen - entscheidend für unsere Wahl ist nur, was wir besser denken können.